Тема 5.4. Структурные характеристики вариационного ряда распределения

Мода и медиана.

Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.

Мода (Мо) – чаще всего встречающийся вариант.

Мода (Мо) – это наиболее часто встречающееся значение признака, или иначе говоря, значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по-разному.

Для интервального ряда:

где 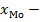нижняя граница модального интервала;

величина интервала;

частота модального интервала;

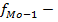частота интервала, предшествующего модальному;

частота интервала, следующего за модальным.

Для дискретных рядов распределения модой является значение признака, которому соответствует наибольшая частота.

Мода зависит от величины групп, от точного положения границ групп.

Определить модальное значение признака можно и по графику. Для этого в случае дискретных вариационных рядов строится полигон распределения. Значение абсциссы, соответствующее наибольшей вершине полигона, будет значением моды.

Если имеется интервальный вариационный ряд с равными интервалами, то для определения моды строится гистограмма, у которой на оси абсцисс находятся значения границ интервалов, а на оси ординат – соответствующие интервалам частоты. На гистограмме модальный интервал будет иметь наибольшую высоту столбца. Затем надо провести линии, соединяющие вершины модального столбца с прилегающими вершинами соседних столбцов. Для нахождения значения моды из точки пересечения проведенных линий на ось абсцисс опускается перпендикуляр. Абсцисса точки пересечения будет значением моды.

Медиана (Me)– это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.

Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения.

Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.

Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.

Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал.

Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.

Для определения медианы в интервальном ряду сначала находится медианный интервал. Для этого находится порядковый номер медианы . Накопленная частота, которая равна номеру медианы или первая его превышает, в интервальном вариационном ряду соответствует медианный интервал.

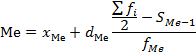
где нижняя граница медианного интервала;

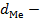величина медианного интервала;

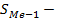накопленная частота интервала, предшествующего медианному;

частота медианного интервала.

Раздел 6. Ряды динамики в статистике

Дата добавления: 2015-05-26