Обернена матриця

Приклад.

Задано матричні лінійні перетворення: B = A X;

X = B Y; Y = C Z.

Потрібно виразити вектор B через вектор Z. Для цього досить зробити послідовні підстановки;

B = A·X = A·B·Y = A·B·C·Z.

Якщо глянути на запис системи лінійних рівнянь у матричній формі

A X = B (1.39)

те для визначення вектора невідомих X напрошується аналогія звичайної алгебри:

x = b/a, (1.40)

де b і a – скалярні величини.

Дійсно, було б дуже зручно знайти вектор невідомих Х за допомогою матричної операції, подібної до виразу (1.40). Але, на жаль, операція ділення в матричній алгебрі не визначена.

У матричній алгебрі існує матриця, за допомогою якої, за виразом аналогічному за формою (1.40), знаходять невідомі системи лінійних рівнянь. Називається така матриця оберненою.

Названа так ця матриця за аналогією з оберненою величиною елементарної алгебри. Нагадаємо, що в алгебрі, оберненою до 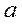є величина , що позначається . Вихідна величина і до неї обернена 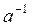зв'язані чудовою властивістю:

, (1.41)

яке і дало назву зворотній матриці.

¨	Визначення. У матричній алгебрі квадратну матрицю, що позначається таку, що помножена зліва чи справа на вихідну матрицю дає одиничну матрицю Е, називають оберненої по відношенню до А. Обернену матрицю позначають таким же символом, яким позначена обернена матриця, але з показником ступеня - 1.

Отже, матриця 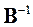, підлегла правилу:

і (1.42)

називається оберненою по відношенню до

Навіщо потрібна обернена матриця?

За допомогою оберненої матриці отримують значення вектора невідомих за формулою:

, (1.43)

де - обернена до заданої матриці системи лінійних рівнянь ;

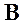- вектор вільних членів заданої системи лінійних рівнянь.

Одержання оберненої матриці A ^-1 називається обертанням матриці A. Способів обертання матриць зараз розроблено багато. Одним із самих популярних є спосіб, заснований на алгоритмі виключення Гаусса-Жордана. Тут не розглядається обертання матриць, ми відсилаємо читача до численної літератури з цього питання.

Закінчуючи визначення оберненої матриці, зауважимо, що не кожна матриця може мати собі обернену, як і не кожна система лінійних рівнянь має розв’язок.

Отримання оберненої матриці шляхом багаторазового розв’язку заданої системи

Одним із найпопулярніших є спосіб, заснований на алгоритмі багатократного розв’язку n систем рівнянь, утворених із заданої матриці порядку n та з n векторами правої частини, які містять нулі у всіх строках, за виключенням i –той строки, яка містить 1, i = 1,2,...n.

Цю ідею отримання оберненої матриці пояснимо за допомогою прикладу.

Задана матриця [A]. Потребується отримати обернену до неї.
Формуємо систему рівнянь
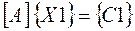
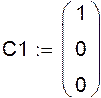
Розв’язок цієї системи, тобто вектор буде першим стовбцем шуканої оберненої матриці
Формуємо другу систему рівнянь
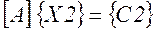
Розв’язок цієї системи, тобто вектор 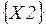є другий стовбець шуканої оберненої матриці
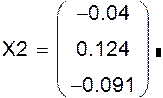
Формуємо третю систему рівнянь
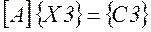
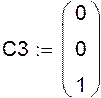
Розв’язок цієї системи, тобто вектор 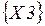є третій стовбець шуканої оберненої матриці
Отримані три вектори розв’язків складають три стовбці шуканої оберненої матриці

В тому, що отримана матриця є дійсно оберненою до , легко переконатися, якщо їх перемножити:

Як видно, результат множення є одинична матриця. Отже, отримана матриця А^-1, дійсно, є оберненою до заданої матриці А, згідно визначення (див.).

Нарешті відмітимо, що програмний комплекс MathCAD має вбудовану стандартну функцію обернення матриць. Записується вона так, як і звичайно в матричній алгебрі, тобто вводиться символ вихідної матриці і додається символ ступеня – 1.

Дата добавления: 2015-05-26