Математичний опис методу скінчених елементів

Метод скінчених елементів – енергетичний, варіаційний, тобто, що полягає в чисельному визначенні функції, що є наближеним з будь-яким ступенем точності, розв’язком крайової задачі. Розглянемо процедуру одержання рівнянь, для одного елемента і рівнянь, які описують поведінку всієї заданої системи.

Диференціальні рівняння, що описують крайові задачі механіки в переміщеннях, будемо записувати в операторному виді:

(5.1)

де 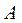– матриця диференціальних операторів крайової задачі;

– вектор невідомих функцій переміщень, що підлягають визначенню при заданих граничних умовах;

– вектор заданих функцій зовнішніх навантажень.

¨	Термінологія. Задача пошуку розв’язку диференціального рівняння (або системи диференціальних рівнянь) при заданих граничних умовах, називається крайовою задачею. Розв’язком крайової задачі є функція, що задовольняє диференціальному рівнянню (рівнянням) і заданим граничним умовам.

Запишемо функціонала, зв'язаний з диференціальним рівнянням крайової задачі (5.1):

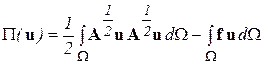, (5.2)

де 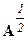- матриця диференціальних операторів, порядок яких у два рази нижче ніж порядок операторів вихідної матриці А, а - область визначення крайової задачі

Так, наприклад, якщо вихідний оператор є 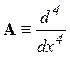то

Функціонал (5.2). має чіткий фізичний зміст: це повна потенційна енергія системи. Першим інтегралом визначається робота внутрішніх сил, другим – робота зовнішніх сил.

Далі в пошуках дискретного розв’язку розчленуємо задану систему на r елементів. Нехай кожен елемент містить 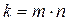ступенів свободи (тут m – кількість вузлів, що належать одному елементу; n – кількість ступенів свободи в одному вузлі).

¨	Термінологія. Ступені свободи – незалежні параметри, що визначають положення тіла в просторі. У випадку нашої крайової задачі – це лінійні (поступальні) і кутові переміщення вузлів дискретного елемента.

Функціонал, тобто потенційну енергію системи (5.2), представимо у вигляді суми

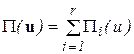, (5.3)

де – повна потенційна енергія i-го елемента. Функція переміщень u, через яку виражається функціонал (5.2), невідома і нею потрібно задатися. Вибір функції u, що називається координатою, - самий відповідальний етап у побудові скінченно-елементного розв’язку. Приймемо координатну функцію i-го елемента в найбільш загальній формі чисельного прямого методу

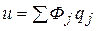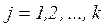, (5.4)

де q_j – ступені свободи системи, що підлягають визначенню;

Ф_j – апріорно прийняті функції, що апроксимують поле розподілу ступенів свободи в межах одного елемента. У загальному випадку Ф_j=Ф_j(x,y,z); k – кількість ступенів свободи одного елемента.

Внесемо значення координатної функції (5.4) у вираз функціонала (5.3), отримаємо 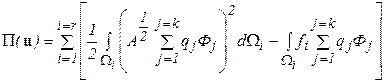(5.5)

Тепер функціонал (5.5) являє собою функцію t незалежних змінних – ступенів свободи:

, де t = k. r (5.6)

Функціонал (5.5) досягає мінімуму при значеннях ступенів свободи, що перетворюють у нуль його перші похідні по ступенях свободи q_j: Відповідно до (5.3) пошук мінімуму можна виконати послідовно, відносно кожного із елементів. Для i-го елемента маємо:

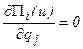, j = 1,2,3, …, k (5.7)

Обчисливши часткові похідні і дорівнявши їх до нуля, отримаємо вираз, що зв'язують ступені свободи (вузлові переміщення) одного елемента з вузловими силами.

Обчисливши часткові похідні і дорівнявши їх до нуля, отримаємо вирази, що зв'язують ступені свободи (вузлові переміщення) одного елемента з вузловими силами. Після диференціювання функціонала (5.7) отримаємо k спільних лінійних рівнянь такого виду

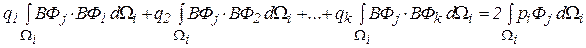(5.8)

Тут для зручності написання виразу (5.8) введено позначення 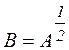; p_i - функція навантаження i – го елемента.

Далі систему рівнянь (5.8) перепишемо ще раз, застосувавши такі позначення

, s = 1,2, …, k 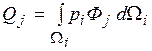, j = 1,2, …, k (5.9)

В матричній формі система рівнянь (5.8), з урахуванням прийнятих позначень (5.9) записується так

(5.10)

Розв’язок рівняння (5.10) відносно вектора невідомих ступенів свободи q (тобто значення невідомих переміщень q_j,) і є шуканий розв’язок дискретної задачі для одного i-го елемента. Дійсно, розв’язавши систему (5.10) щодо невідомих ступенів свободи q_j, знайдемо такі значення, які доставляють мінімум функціоналу П _i (u). Отже вектор q системи (5.10), є розв’язком диференціального рівняння крайової задачі (5.1) для i-го елемента.

Будемо записуватися систему рівнянь (5.10) у вигляді

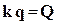, (5.11)

де - матриця жорсткості елемента;

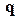- вектор невідомих ступенів свободи;

- вектор вузлових сил.

Рівняння (5.11) – є рівнянням рівноваги для одного елемента. Квадратна матриця k, яка зв'язує невідомі вузлові переміщення 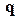з вектором вузлових сил , лінійно перетворює переміщення у вузлові сили.

¨

Термінологія. Квадратна матриця, що зв'язує в рівнянні рівноваги вузлові переміщення з вузловими силами, називається матрицею жорсткості. Компонента матриці жорсткості kij є реакція в зв'язку i від одиничного переміщення, прикладеного за напрямком зв'язку j. Матриця жорсткості, в силу теореми Бетті, симетрична, її коефіцієнти мають взаємність: kij = kji. У будівельній механіці стержньових систем матриця жорсткості відома більш як 100 років, тобто задовго до появи методу скінчених елементів (1956 р.).

Система рівнянь методу скінчених елементів усієї конструкції записується у вигляді:

, (5.12)

де – глобальна матриця жорсткості всієї конструкції;

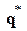– вектор ступенів свободи;

– вектор вузлових сил.

Система рівнянь (5.12) – особлива і не може бути розв’язана відносно невідомих ступенів свободи. Для того щоб отримати розв’язок, потрібно попередньо врахувати граничні умови. Мова йде про те, що частина з компонентів вектора ступенів свободи 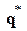дорівнює нулю. Це переміщення в місцях опор (у противному випадку конструкція не закріплена в просторі). Процедура врахування граничних умов полягає у викреслюванні рядків і стовпців, що відповідають напрямкам, по яких задані переміщення, які дорівнюють нулю.

Позначимо матрицю жорсткості, перебудовану відповідно до граничних умов K ^*, і остаточно запишемо систему рівнянь методу скінченних елементів у формі методу переміщень:

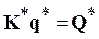(5.13)

Вектор вузлових сил 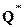у (5.13) формується шляхом підсумовуванням сил по кожному з елементів, для яких j-я ступінь свободи є спільною

, (5.14)

де – визначається за другою з формул (5.9).

Розв’язавши систему лінійних рівнянь (5.13), отримаємо значення ступенів свободи, якими визначається напружений стан конструкції. Далі за відомими залежностями теорії пружності обчислюють деформації чи напруги та зусилля.

Рівняння (5.13) варто розглядати як дискретний аналог реальної конструкції. Склавши рівняння МСЕ, тим самим перейдемо від реальної системи з нескінченним числом ступенів свободи до уявної системи із скінченним числом ступенів свободи.

Підсумовуючи вищевикладене, можна виділити такі основні положення концепції методу скінчених елементів:

· задану конструкцію розчленовують на елементи скінчених розмірів;

· для типових елементів, задавшись попередньо формою функції, що апроксимує поле переміщень(ф. 5.4), отримують матрицю жорсткості;

· з матриць жорсткості елементів одержують матрицю жорсткості всієї конструкції (ф.5.12);

· отриману матрицю жорсткості трансформують з урахуванням умов закріплення конструкції в просторі, одержують глобальну матрицю жорсткості K ^*;

· будують вектор вузлових сил Q ^* (ф. 5.14). Якщо зовнішні сили задані по області елемента, їх попередньо приводять до еквівалентних вузлових;

· розв’язують систему лінійних рівнянь МСЕ (ф. 5.13), одержують значення вектора вузлових переміщень q * -дискретного аналога заданого об'єкта;

· за значеннями вектора вузлових переміщень q *, використовуючи класичні залежності механіки твердого деформованого тіла, одержують деформації, напруги і зусилля.

Далі основні положення методу скінчених елементів розглядаються докладніше.

Дата добавления: 2015-05-26