
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Складний процент
|
|
|
|
Складний процент – процент, який нараховується на суму, що інвестується на початку, та нараховані в попередні періоди проценти.
Начислення проценту один раз у рік:
 (6)
(6)
Нарахування процентів декілька разів у рік:
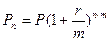 (7)
(7)
де m – періодичність нарахування проценту впродовж року.
Безперервне нарахування проценту:
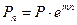 (8)
(8)
де Pn – безперервно нарахований процент;
n – період часу нарахування проценту;
e = 2,71828…
1.1.3 Еквівалентний та ефективний проценти
Ефективний (реальний) процент – процент, який дістається за підсумкам року при нарахуванні складного проценту в межах року.
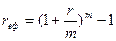 (9)
(9)
де rеф – ефективний процент;
r – простий процент в розрахунку на рік, який задається за умовами фінансового інструменту.
Еквівалентний ефективний простий процент в розрахунку на рік:
 (10)
(10)
1.1.4 Еквівалентність безперервно нараховуємого проценту та проценту, який нараховується m разів на рік
Еквівалентність між двома видами процентів можна знайти, коли дорівнювати суми, які отримують з розрахунком безперервно нараховуємого проценту та нарахування проценту m раз на рік.
 (11)
(11)
1.1.5 Комбінація простого та складного процентів
Проценти капіталізуються (тобто приєднуються до основної суми рахунку, на яку нараховуються проценти) у кінці кожного року. Впродовж року нараховується простий процент.
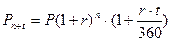 (12)
(12)
де Pn+t – сума, яку отримає інвестор за n років та t днів;
P - початкова сума, яка інвестується;
t – число днів, за який нараховується простий процент;
r – процент, який нараховується впродовж року.
1.2 Дисконтована вартість
В фінансових розрахунках виникає необхідність порівнювати між собою різні суми грошей в різні моменти часу. Для цього їх необхідно привести до спільного часового знаменника, тобто початковій точці підрахунку. При нарахуванні складного проценту:
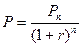 (13)
(13)
де Pn – майбутня вартість;
P – дисконтована (приведена) вартість;
 - коефіцієнт дисконтування.
- коефіцієнт дисконтування.
При нарахуванні складного проценту m разів на рік:
 (14)
(14)
Для безперервно нараховуємого проценту:
 (15)
(15)
Дисконтована вартість для простого проценту:
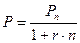 (16)
(16)
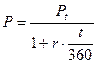 (17)
(17)
 (18)
(18)
1.3 Визначення періоду нарахування проценту
Для простого проценту:
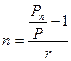 (19)
(19)
 (20)
(20)
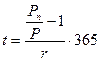 (21)
(21)
Для складного проценту період часу інвестування:
 (22)
(22)
1.4 Визначення майбутньої вартості потоку платежів
Якщо інвестор у кінці кожного року впродовж визначеного періоду часі отримує неоднакові платежі та буде інвестувати суму кожного платежу на час до закінчення даного періоду, то по його завершенні він отримає суму, яку називають майбутньою вартістю потоку платежів:
 (23)
(23)
де F – майбутня вартість потоку платежів;
Ct – сума платежу за рік t;
r – процент, під який інвестується сума Ct;
n – кількість років, впродовж який робляться виплати.
1.5 Аннуітет
Аннуітет (рента) – це потік однакових по сумі платежів, які здійснюються з однаковою періодичністю. Якщо платежі здійснюються в кінці кожного періоду, аннуітет називається відкладеним, а якщо на початку кожного періоду, то це терміновий аннуітет.
1.5.1 Майбутня вартість аннуітету
Майбутня вартість аннуітету при нарахуванні складного проценту один раз на рік:
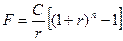 (24)
(24)
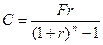 (25)
(25)
Майбутня вартість аннуітету при здійсненні виплат m разів на рік:
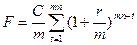 (26)
(26)
де С – величина виплати за рік.
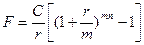 (27)
(27)
Майбутня вартість аннуітету при нарахуванні проценту m разів на рік:
 (28)
(28)
1.5.2 Приведена вартість аннуітету
При нарахуванні проценту один раз на рік приведена вартість аннуітету представляє собою майбутню вартість аннуітету, дисконтовану до моменту його заснування, тобто на величину  :
:
 (29)
(29)
де Р – приведена вартість аннуітету.
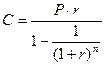 (30)
(30)
Приведена вартість аннуітету при здійсненні виплат m раз на рік:
 (31)
(31)
Приведена вартість аннуітету при нарахуванні проценту m раз на рік:
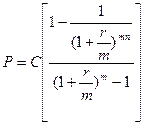 (32)
(32)
1.5.3 Вічна рента
Вічна рента допускає, що платежі будуть здійснюватись завжди. Майбутню вартість такого аннуітету визначити неможливо.
Приведена вартість для вічної ренти для n→∞:
 (33)
(33)
1.5.4 Терміновий аннуітет
Майбутня вартість термінового аннуітету при нарахуванні складного проценту один раз на рік:
 (34)
(34)
де Fn – майбутня вартість термінового аннуітету;
n – кількість років, впродовж яких виплачується аннуітет.
Приведена вартість термінового аннуітету:
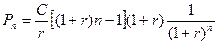 (35)
(35)
або

1.6 Прибутковість
У загальному виді показник прибутковості визначається як відношення отриманого результату до витрат, яка принесли даний результат. Прибутковість виражають в процентах.
1.6.1 Прибутковість за період
Прибутковість за період – це прибутковість, яку інвестор отримує за визначений період часу.
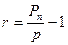 (36)
(36)
де r – прибутковість за період;
P – початково інвестовані кошти;
Pn – сума, яка отримана через n років.
1.6.2 Прибутковість в розрахунку на рік
При необхідності порівняння прибутковості різноманітних фінансових інструментів використовують прибутковість в розрахунку на рік.
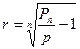 (37)
(37)
r – прибутковість в розрахунку на рік;
n – число років.
Якщо складний процент нараховується m разів на рік, то прибутковість за рік визначається:
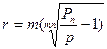 (38)
(38)
Якщо процент розраховується безперервно, то прибутковість в розрахунку на рік визначається:
 (39)
(39)
Для короткострокових операцій:
 (40)
(40)
та
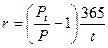 (41)
(41)
Для короткострокових цінних паперів можна розрахувати ефективну прибутковість:
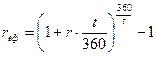 (42)
(42)
або
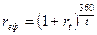 (43)
(43)
де t – період фінансової операції (час з моменту покупки до продажу або погашення цінного паперу);
r – простий процент в розрахунку на рік;
rt – прибутковість за період t.
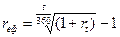 (44)
(44)
1.6.3 Процентні ставки та інфляція
Номінальна процентна ставка – процентна ставка без врахування інфляції.
Реальна процентна ставка – ставка, яка скоректована на процент інфляції.
Рівняння Фішера представляє взаємозв’язок між номінальною та реальною процентними ставками.
 (45)
(45)
де r – номінальна ставка процента;
y – реальна ставка процента;
i - темп інфляції.
Контрольні запитання
1 У чому різниця між простим і складним відсотками?
Задачі для закріплення матеріалу
1 Вкладник розміщає на рахунку в банку 100 тис. грн. Яку суму він одержить через 60 днів, якщо банк нараховує по внеску 10% річних?
2 Прибутковість фінансового інструменту на базі 365 днів дорівнює 20% річних. Перерахуйте його прибутковість з розрахунку 365 днів.
3 Вкладник розміщає на рахунку в банку 100 тис. грн. Яку суму він одержить через 2 роки, якщо банк нараховує по внеску 10% річних? Відсотки капіталізуються щорічно.
4 Вкладник розміщає на рахунку в банку 100 тис. грн. Яку суму він одержить через 2 роки, якщо банк нараховує по внеску 10% річних? Відсотки капіталізуються через кожні півроку.
5 Вкладник розміщає на рахунку в банку 100 тис. грн. Яку суму він одержить через 60 днів, якщо банк нараховує по внеску 10% річних на умовах безперервного нарахування відсотків?
6 По банківському рахунку встановлені 10% річних. Відсоток нараховується щокварталу. Розрахуйте ефективний відсоток.
7 10% річних нараховуються чотири рази в рік. Визначте еквівалентний відсоток, що безупинно нараховується.
8 Вкладник розміщає на рахунку в банку 100 тис. грн. Яку суму він одержить через 2 роки 60 днів, якщо банк нараховує по внеску 10% річних? Відсотки капіталізуються щорічно.
9 Банк нараховує 10% річних. Відсотки капіталізуються щорічно. Яку суму вкладник повинний розмістити в банку, щоб через 5 років одержати на рахунку 100 тис. грн.
Задачі для самостійного опрацювання
1 Інвестор протягом 10 років наприкінці кожного року одержує суму 50 тис. грн. і розміщає кожен платіж до закінчення десятилітнього періоду під 10% річних. Визначите майбутню вартість аннуітету.
2 Пенсійний фонд через 10 років повинний акумулювати 1млрд. грн. Визначте розмір щорічних внесків у пенсійний фонд, якщо до закінчення указаного періоду вони інвестуються під 10% річних.
3 Інвестор протягом 10 років наприкінці кожного року одержує суму 50 тис. грн. і розміщає кожен платіж до закінчення десятиліт нього періоду під 10% річних. Визначте приведену вартість аннуітету.
4 Позичальник бере кредит на 10 років у розмірі 100 млн. грн. під 25% річних з умовою погашення його рівними сумами наприкінці кожного року. Визначте величину щорічних виплат по кредиту?
5 Скільки коштує вічна рента, якщо по ній щорічно виплачується 50 тис. грн.? Банківський відсоток дорівнює 10% річних.
6 Вкладник інвестував 50 тис. грн. і одержав через 4 роки 200тис. грн. Визначте прибутковість його операції за чотири роки
7 Визначте за умовами задачі 16 прибутковість операції інвестора в розрахунку на рік.
8 Вкладник інвестував 50 тис. грн. і одержав через 100 днів 60 тис. грн. Визначте ефективну прибутковість його операції на базі 365 днів.
9 Номінальна ставка відсотка дорівнює 10% річних, темп інфляції - 5%. Визначте реальну ставку відсотка.
ТЕМА 2. ВИЗНАЧЕННЯ КУРСОВОЇ ВАРТОСТІ ТА
ПРИБУТКОВОСТІ ЦІННИХ ПАПЕРІВ
Мета роботи: ознайомитися з технікою розрахунків курсової вартості та прибутковості цінних паперів.
2.1 Визначення курсової вартості та прибутковості облігацій
Техніку визначення курсової вартості можна представити трьома етапами:
1) визначення потоку доходів, який очікується по цінному паперу;
2) визначення дисконтованої вартості величини кожного платежу за папером;
3) визначення сумарної дисконтованої вартості.
2.1.1 Визначення курсової вартості купонної облігації
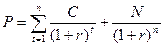 (46)
(46)
де P – ціна облігації;
C – купон;
N – номінал;
n – число років до погашення облігації;
r – прибутковість до погашення облігації.
Прибутковість до погашення – це прибутковість в розрахунку на рік, яку забезпечить собі інвестор, якщо, купив облігацію, протримає її до погашення.
Найбільш важливим моментом при розрахунку ціни являється визначення ставки дисконтування, яка відповідає рівню ризику інвестицій.
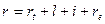 (47)
(47)
де rt – ставка без ризику;
l – премія за ліквідність;
i – темп інфляції;
re – реальна ставка проценту.
Якщо купон за облігацією виплачується частіше, ніж один раз на рік:
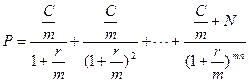 (48)
(48)
Якщо уявити, що виплата купонів – це аннуітет, то:
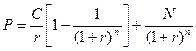 (49)
(49)
та
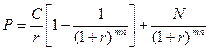 (50)
(50)
Якщо купон виплачується один раз на рік, то ціна облігації визначається:
 (51)
(51)
де V=t /365;
t – число днів з моменту угоди до виплати чергового купона;
n – ціле число років, які залишаються до погашення облігації, включно поточний рік.
2.1.2 Визначення курсової вартості середньострокової та довгострокової безкупонної облігації
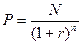 (52)
(52)
Якщо до погашення облігації залишається не ціле число років:
 (53)
(53)
t – число днів з моменту угоди до початку цілого річного періоду для облігації;
n – ціле число років, які залишаються до погашення облігації, включаючи поточний рік.
2.1.3 Визначення прибутковості облігації
Поточна прибутковість купонної облігації:
 (54)
(54)
де rt – поточна прибутковість;
С – купон облігації;
Р – поточна ціна облігації.
Прибутковість до погашення враховує на тільки купон та ціну паперу, але й період часу, який залишається до погашення, а також знижки або премії відносно номіналу.
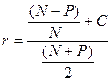 (55)
(55)
де r – прибутковість до погашення;
N – номінал облігації;
P – ціна облігації;
n – число років до погашення;
C - купон.
Прибутковість до погашення безкупонної облігації:
2.1.4 Реалізований процент
Реалізований процент розраховується з врахуванням усіх надходжень, які інвестор зможе отримати за час володіння облігацією.
Загальна сума засобів по облігації складається з трьох елементів:
1) суми погашення при викупі облігації або суми від її продажу;
2) купонні проценти;
3) проценти від реінвестування купонів.

де Ср – сума купонних платежів та процентів від реінвестування купонів;
С – купон облігації;
n – число періодів, за які виплачуються купони;
r – процент, під який вкладник планує реінвестувати купонні платежі.
Реалізований процент – це процент, який дозволяє дорівнювати суму усіх майбутніх надходжень, які інвестор планує отримати по облігації, до її сьогоднішньої ціни.
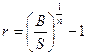 (57)
(57)
де В – усі майбутні надходження;
S – ціна покупки облігації.
2.1.5 Дюрація
Дюрація Макуолі представляє собою еластичність ціни облігації за процентною ставкою і тому служить мірою ризику зміни ціни облігації при зміні процентної ставки.
Щоб визначити цей показник, необхідно взяти першу похідну по r для формули визначення ціни облігації та перетворити її.
 (58)
(58)
де Р – ціна облігації;
dP – зміна ціни облігації;
dr – зміна прибутковості до погашення;
r – прибутковість до погашення;
C – купон облігації;
N – номінальна облігація;
n – число років до погашення облігації.
Величина  називається дюрацією Макуолі (Д):
називається дюрацією Макуолі (Д):
 (59)
(59)
Якщо купони виплачуються m разів у рік, то дюрація в роках визначається:
Д = дюрація в m періодах / m (60)
 (61)
(61)
Величина 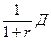 називається модифікованою дюрацією.
називається модифікованою дюрацією.
 (62)
(62)
2.2 Визначення курсової вартості та прибутковості акцій
2.2.1 Визначення курсової вартості акцій
Ціна звичайної акції визначається дисконтуванням дивідендів, які будуть виплачені за нею.
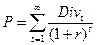 (63)
(63)
де Р – ціна акції;
Divt – дивіденд, який буде виплачений в періоді t;
r – ставка дисконтування (прибутковість).
Якщо інвестор планує в майбутньому продати акцію, то її вартість можна оцінити:
 (64)
(64)
де Pn – ціна акції у кінці періоду n, коли інвестор планує продати її.
Дивіденд для любого року в найпростішої моделі прогнозування дивідендів розраховується:
 (65)
(65)
де Div0 – дивіденд за поточний рік;
g – темп приросту дивіденду.
Курсова вартість акції з врахуванням росту дивідендів:
 (66)
(66)
де Divt – дивіденд майбутнього року.
r > g.
2.2.2 Визначення прибутковості акції
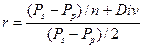 (67)
(67)
r – прибутковість від операції з акцією;
Ps – ціна продажу акції;
Pp – ціна покупки акції;
Div – середній дивіденд за n років (середнє арифметичне);
n – число років від покупки до продажу акції.
Якщо покупка та продаж акції відбуваються в рамках одного року, то прибутковість операції визначається:
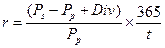 (68)
(68)
де t – число днів з моменту покупки до продажу акції.
2.3 Визначення курсової вартості та прибутковості векселя
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 1110; Нарушение авторских прав?; Мы поможем в написании вашей работы!