Уравнение процесса

Политропные процессы

До сих пор рассматривались процессы, у которых имелись вполне определенные признаки: изохорный процесс осуществлял­ся при постоянном объеме; изобарный — при постоянном давле­нии; изотермический — при постоянной температуре; адиабат­ный— при отсутствии теплообмена между рабочим телом и внеш­ней средой. Наряду с этими процессами можно представить еще бесконечное множество процессов, у которых имеются другие постоянные признаки.

Условились всякий процесс идеального газа, в котором удель­ная теплоемкость является постоянной величиной, называть политропным процессом, а линию процесса — политропой.

Из определения политропного процесса следует, что основные термодинамические процессы — изохорный, изобарный, изотерми­ческий и адиабатный,— если они протекают при постоянной удель­ной теплоемкости, являются частными случаями политропного процесса. Итак, политропный процесс проходит при постоянной теплоемкости.

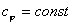
Если теплоемкость зависит от температуры, то нужно найти среднюю теплоемкость, чтобы процесс стал политропным.

Для исследования процесса и расчета слагаемых I закона термодинамики нужно установить связь между параметрами состояния в политропном процессе. Эта функция называется уравнением политропы. Запишем уравнение I закона термодинамики, преобразуем

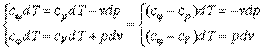
и поделим почленно

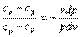
Так как 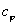= const в процессе, то левая часть 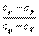= const и называется показатель политропы:

n = ,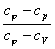

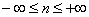
При этом, каждому значению n соответствует некоторый конкретный процесс.

Получили дифференциальное уравнение:

n=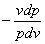

Разделяем переменные

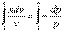
и интегрируем в пределах процесса

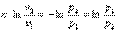
Потенцируем

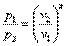или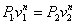

Это выражение выполняется не только для крайних точек процесса, но и для всех промежуточных. Оно называется уравнением политропы:

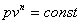
Запишем это уравнение через другие параметры P-T и V-T:

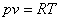
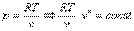
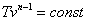
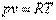
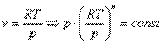
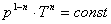
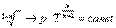
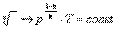
Дата добавления: 2015-05-26