Ньютоновские жидкости

Величина вязкого (внутреннего) трения при сдвиговом течении определяется касательным напряжением 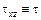, которое требуется приложить к верхней пластине 2 для того, чтобы поддерживать течение с определенным градиентом скорости 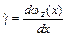, имеющим размерность [1/с] и (в случае одноосного сдвигового течения) называемым скоростью сдвига.

Вязкость – это мера интенсивности противодействия возникающих в жидкости сил внутреннего трения F сдвиговому течению этой жидкости. Физическая величина, обычно называемая динамической вязкостью μ, в действительности представляет собой коэффициент, входящий в соотношение ,

где F – сила, действующая по касательной к поверхности площадью S; 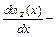скорость сдвига (градиент скорости в направлении оси x, ориентированной нормально (перпендикулярно) направлению течения); μ – коэффициент, называемый динамической вязкостью; ω _z – компонент вектора скорости в направлении оси z.

Если ввести обозначения: 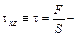касательное напряжение (напряжение сдвига), представляющее собой отношение силы F, действующей в направлении оси z на поверхность (ориентированную нормально к оси х), к величине площади S этой поверхности; 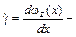скорость сдвига,

то формулу (8.2) можно представить в виде [33]: .

Формула (8.3) выражает так называемый закон течения Ньютона применительно к условиям одноосного (одномерного) сдвига. Жидкости, течение которых подчиняется закону Ньютона (8.3), называют ньютоновскими жидкостями [33].

Кроме ньютоновских жидкостей есть большое количество жидкостей, течение которых не подчиняется закону Ньютона (8.3). Такие жидкости обычно называют неньютоновскими жидкостями [33].

Механическое поведение текучих систем (ньютоновских и неньютоновских) при их сдвиговом течении можно графически представить двумя видами зависимостей [33], приведенными на рис. 8.2.

Рис. 8.2 Графическое представление течения ньютоновских жидкостей:

а – в виде зависимости касательного напряжения сдвига τ от скорости сдвига ;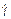

б – в виде зависимости динамической вязкости μ от скорости сдвига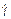

На рис. 8.2, а показана зависимость касательного напряжения τ от скорости сдвига 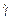для ньютоновской жидкости, подчиняющийся закону (8.3). Такой график называют реологической диаграммой или «кривой течения». Коэффициент динамической вязкости μ на такой «кривой течения» неньютоновской жидкости представляет собой тангенс угла наклона прямой линии (8.3).

Другая интерпретация закона течения Ньютона (8.3) представлена на рис. 8.2, б. В этом случае (см. рис. 8.2, б) графически представляется зависимость динамической вязкости μ от скорости сдвига .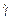

Для ньютоновских жидкостей оба варианта графического отображения закономерностей течения представляют собой прямые линии. Поэтому, при изучении течения ньютоновских жидкостей нет основания отдавать предпочтение одному виду графического отображения по сравнению с другим.

Закон Ньютона (8.3) для несжимаемой жидкости (с постоянной плотностью ρ = const) в результате несложных преобразований можно представить в виде [33]: 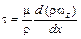Или ,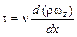

где 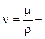коэффициент кинематической вязкости [м²/с], имеющий ту же размерность, что и коэффициент температуропроводности a и коэффициент диффузии a_m, входящие в законы Фурье и Фика; 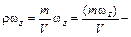величина 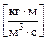, имеющая физический смысл концентрации количества движения (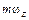) 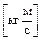в единице объема V [м³]; t – касательное напряжение сдвига, имеющее размерность [t] = = , которое можно интерпретировать как поток количества движения (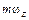) 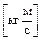через единицу поверхности [м²] в единицу времени [с].

Зависимость в виде (8.3а) наиболее отчетливо выявляет аналогию закона Ньютона с другими известными феноменологическими законами переноса субстанции, в частности, с законом теплопроводности Фурье и законом диффузии Фика ,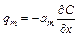

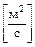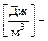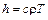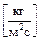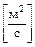где q , a , h соответственно тепловой поток q, коэффициент температуропроводности a и объемная энтальпия , имеющая физический смысл концентрации тепловой энергии в единице объема; q_m , a_m , с соответственно поток вещества через единицу поверхности в единицу времени, коэффициент диффузии a_m и концентрация c диффундирующего вещества в единице объема.

Слева в каждом из законов (8.3а), (8.4) и (8.5) стоят потоки (количества движения (m w _z), количества тепла Q и количества вещества m) через единицу поверхности в единицу времени, а справа – составляющие градиентов движущих сил, представляющих собой концентрацию переносимой субстанции 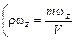, , 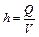в единице объема V. При этом коэффициент кинематической вязкости 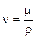, входящий в закон (8.3а), можно трактовать как коэффициент диффузии количества движения (m w _z) по аналогии с тем, что коэффициенты a и a_m, входящие в законы Фурье (8.4) и Фика (8.5), обычно рассматривают как коэффициенты диффузии количества тепла Q и количества вещества m. Отметим, что коэффициенты ν, a и a_m, входящие в законы Ньютона (8.3а), Фурье (8.4) и Фика (8.5), имеют одинаковую размерность м²/с.

Дата добавления: 2015-05-26