Загальні вказівки. Завдання 2 Планування ДФ та ПФ експерименту

Завдання 2 Планування ДФ та ПФ експерименту

Якщо наперед не відомий аналітичний вираз функції відгуку, то можна розглядати не саму функцію, а її розкладання, наприклад в статечній ряд у вигляді полінома

Y=В₀ + B₁Х₁ + … + B_nХ_n + В₁₂Х₁Х₂ + … В_nn-1Х_nХ_n-1 + В₁₁Х₁² + … + В_nnX_n² +….

Розкладання в статечній ряд функції можливо в тому випадку, якщо сама функція є безперервною і гладкою. На практиці зазвичай обмежуються числом членів статечного ряду і апроксимують функцію поліномом деякої міри.

Зв'язок між кодовим і натуральним виразом чинника задається формулою

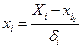, (2.1)

де - натуральне значення чинника;

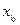- значення 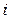-го чинника на нульовому рівні;

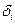- інтервал варіювання 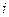-го чинника.

Перевірка відтворюваності дослідів. При однаковому числі паралельних дослідів на кожному поєднанні рівнів чинників відтворюваність процесу, перевіряється по критерію Кохрена:

, (2.2)

де 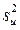дисперсія, що характеризує розсіяння результатів дослідів на -м поєднанні рівнів чинників:

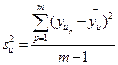
. (2.3)

де 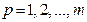- число паралельних дослідів;

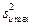- найбільша з дисперсій в строчках плану;

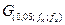- табличне значення критерію Кохрена при 5%-ном рівні значущості;

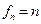- число незалежних оцінок дисперсії;

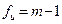- число мір свободи кожної оцінки.

Процес вважається відтворним, якщо виконується нерівність (2.2). При цьому дисперсія відтворюваності (помилка досвіду) визначається по формулі

. (2.4)

Якщо нерівність (2.2) не виконується, то необхідно прийняти заходи до уточнення вимірювань в досвіді з максимальною дисперсією.

У разі відтворного процесу розраховують коефіцієнти регресії

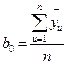. (2.5)

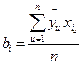. (2.6)

. (2.7)

Перевірка адекватності лінійної моделі виконується за допомогою критерію Фішера. Адекватність обґрунтована, якщо виконується нерівність

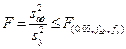, (2.8)

де - розрахункове значення відгуку в 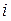-му досвіді;

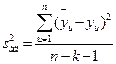, (2.9)

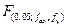- критерій Фішера при 5%-ном рівні значущості;

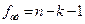- число мір свободи дисперсії адекватності;

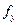- число мір свободи дисперсії відтворюваності.

Оцінка значущості коефіцієнта регресії проводиться за допомогою критерію Стьюдента. Коефіцієнт вважається значущим, якщо виконується нерівність

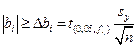, (2.10)

де 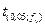- 5%-ная точки розподілу Стьюдента з 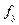мірами свободи.

Якщо в ДФЕ коефіцієнти при взаємодіях не рівні нулю, то знайдені за наслідками дослідів вибіркові коефіцієнти регресії будуть оцінками для сумісних ефектів:

.

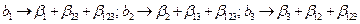Дата добавления: 2015-05-26