Форма входного и остаточного сигналов 3-разрядного последовательного АЦП

РАЗРЯДНЫЙ ПОСЛЕДОВАТЕЛЬНЫЙ АЦП С ДВОИЧНЫМ ВЫХОДОМ

Рис. 3.30

Рис. 3.31

Намного более совершенная архитектура АЦП последовательного счета, основанная на усилителях абсолютной величины (усилители модуля (magnitude amplifiers) или просто MagAmps ™), была разработана Ф. Д. Вальдхауэром (F.D.Waldhauer), Приложение 21. Эта схема часто упоминается, как последовательная схема Грея (serial-Gray) (так как выходное кодирование осуществляется кодом Грея) или поворачивающий (folding) преобразователь (Приложения 22, 23, 24). Функциональная схема основной ступени вместе с ее передаточной функцией представлены на рис.3.32. Принимается, что входной сигнал ступени является линейным пилообразным напряжением, размах которого соответствует диапазону от –V_R до +V_R. Компаратор выявляет полярность входного сигнала и

формирует выходной разряд для данной ступени в виде кода Грея. Компаратор также определяет, должно ли общее усиление ступени быть равным +2 или -2. Опорное напряжение V_R суммируется с выходом коммутатора для генерации остаточного сигнала, который подается на следующую ступень. Полярность остаточного сигнала определяет выходной разряд следующей ступени вновь в виде кода Грея. Передаточная функция поворачивающей (folding) ступени также представлена на рис.3.32.

ЭКВИВАЛЕНТНАЯ СХЕМА КАСКАДА MAGAMP

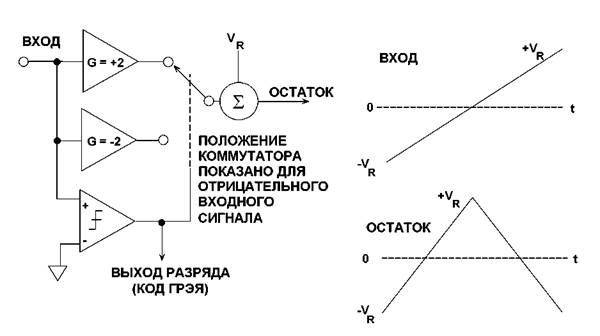
Рис. 3.32

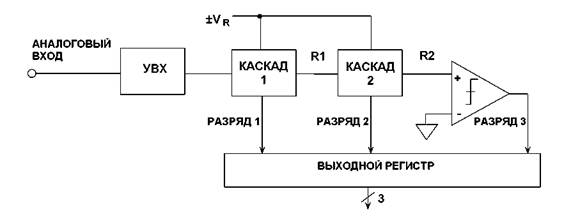
3-разрядный поворачивающий (folding) MagAmp АЦП представлен на рис.3.33, а диаграммы соответствующих остаточных сигналов изображены на рис.3.34. Как и в случае двоичного АЦП с пилообразной формой остаточных сигналов, значение кода Грея для следующей ступени определяется полярностью выходного остаточного сигнала предыдущей ступени. Полярность входного сигнала первой ступени определяет старший значащий разряд кода Грея; полярность выхода R1 — второй разряд кода Грея, полярность выхода R2 — третий разряд кода Грея. Обратите внимание, что, в отличие от двоичного импульсного АЦП, ни одна из ступеней данной архитектуры не дает перепада значения остаточного сигнала. Это делает данную архитектуру перспективной для работы на высоких частотах дискретизации.

Основой функционирования этой архитектуры на высоких скоростях является применение поворачивающей (folding) ступени. Ранние применения данной архитектуры (см. Приложения 22, 23, 24) для генерации поворачивающей функции передачи использовали дискретные операционные усилители с диодами в контуре обратной связи. Современные интегральные схемы реализуют требуемую функцию передачи, управляя коэффициентом усиления по току при разомкнутой обратной связи, что может быть реализовано с более высоким быстродействием. Полностью дифференциальные ступени (включая УВХ) также обеспечивают высокую скорость, более низкие искажения и дают поворачивающие (folding) ступени, обладающие 8-разрядной точностью, не требуя лазерной подстройки тонкопленочного резистора (см. Приложения 25, 26, 27).

БЛОК-СХЕМА 3-РАЗРЯДНОГО АЦП MagAmp™

Рис. 3.33

Дата добавления: 2015-05-26