Составить карту Карно

Цель работы

Цель работы – ознакомление с характеристиками основных логических элементов цифровой схемотехники и изучение методов синтеза комбинационных схем.

Общие сведения

Логические элементы оперируют с сигналами, которые могут принимать значения только двух уровней – высокого и низкого (нулевого). Обычно сигнал высокого уровня обозначают единицей, низкого уровня – нулем. Для описания поведения логических схем используют специальный раздел алгебры – алгебру логики, или булеву алгебру.

Все переменные в алгебре логики могут принимать два значения – “0” и “1”. Наиболее важными функциями алгебры логики являются функции И, ИЛИ, НЕ.

Функция И называется логическим умножением (X₁·X₂) и для двух аргументов описывается табл. 1.

Таблица 1		Таблица 2		Таблица 3
Х1	Х2	(Х1 Х2)		Х1	Х2	(Х1 + Х2)		X

Как видно из таблицы, X₁·X₂ равно 1 только тогда, когда и аргумент X₁, и аргумент X₂ принимают значения 1.

Функция ИЛИ называется логическим сложением (X₁+X₂) и для двух аргументов описывается табл. 2.

Как видно из этой таблицы, (X₁+X₂) равно 1 тогда, когда или аргумент X₁, или аргумент X₂ принимает значение 1.

Функция НЕ – это логическая функция одного аргумента. Она также называется логическим отрицанием X и описывается комбинационной табл. 3.

Логическая функция одного аргумента описывается комбинационной таблицей из 2 строк, двух аргументов – таблицей из 4 строк, n аргументов – комбинационной таблицей из 2 ⁿ строк.

Логическая функция многих аргументов, описывающая соответствующую комбинационную схему, может определяться не только комбинационной таблицей, но и выражением, включающим в себя определенные выше логические функции, например:

При подстановке в выражение (1) значений аргументов определяется значение функции, например: при X₁=0, X₂=1, X₃=1, X₄=1

f (0, 1, 1, 1)=(0+0)(1+1)+1×1×1=0×1+1=0+1=1

По комбинационной таблице можно составить выражение логической функции. Для этого необходимо использовать следующие основные теоремы алгебры логики:

(2)

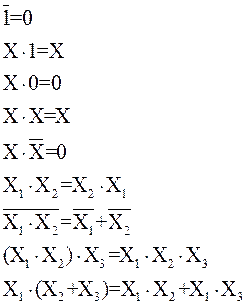
Синтез выражения логической функции

Логические функции с числом переменных не более четырех удобно определять с помощью так называемой карты Карно – формы представления комбинационной таблицы в виде матрицы, строки и столбцы которой соответствуют определению комбинации одной или двух переменных. Например, логическая функция (1), определяемая комбинационной табл. 4, представляется картой Карно (рис. 1).

Таблица 4
X1	X2	X3	X4	Y

		X3X4
X1X2

Р и с. 1. Карта Карно для функции, представленной табл. 4

Карты Карно удобно использовать при синтезе выражения логической функции, задаваемой комбинационной таблицей.

В одном из методов синтеза выражения рассматриваются элементы, содержащие логическую “1”. Если выбрать на карте Карно достаточное количество групп так, чтобы каждый элемент с логической “1” вошел хотя бы в одну группу, то выражение логической функции может быть определено путем использования функции ИЛИ над функциями И, соответствующими выбранным группам. Разумно выбирая группы, можно получать простые выражения. При выборе группы следует руководствоваться следующими принципами: группа должна быть как можно меньше.

Для приведенного выше примера группы могут быть выбраны в соответствии с рис. 2:

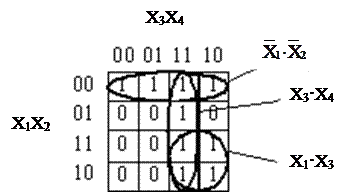
Р и с. 2. Выбор групп на карте Карно для функции,

представленной в табл. 1

В данном случае выбраны три группы

.

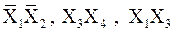Легко убедиться, что функция принимает единичное значение при X₁=0, X₂=0 (первая группа); при X₃=1, X₄=1 (вторая группа); при X₁=1, X₃=1 (третья группа).

Выражение, описывающее логическую функцию (1), имеет вид:

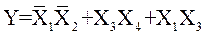(3)

Выбирая группы, необходимо иметь в виду, что крайние столбцы Карно (левый и правый) являются соседними, поскольку Карно является разверткой на плоскость поверхности пространственной фигуры. То же самое можно сказать и про крайние строки (верхнюю и нижнюю).

В этом случае группы могут быть “разорванными” (рис. 3).

Функции, представленные картами на рис. 3, а и рис. 3, б определяются выражениями соответственно

, .

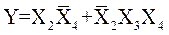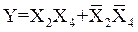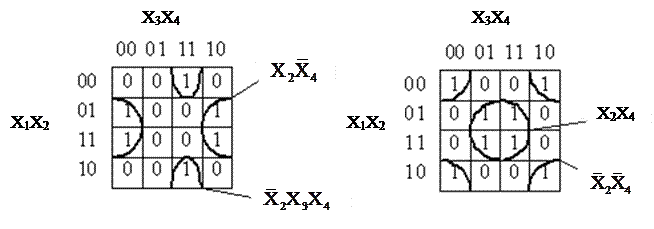
аб

Р и с. 3. Пример карт Карно с разорванными группами

В другом методе синтеза выражения для инверсии логической функции выбираются группы с элементами, содержащими 0.

При выборе групп и синтеза выражения руководствуются принципами, приведенными выше. В качестве примера рассмотрим функцию, представленную картой на рис. 4.

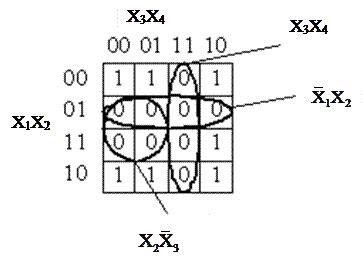Р и с. 4. Карта Карно для функции, содержащей нули в группах

Выражение для инверсии логической функции имеет вид:

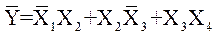
Отсюда определяется выражение логической функции

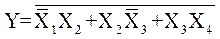
Полученные выражения для логических функций могут быть реализованы с помощью логических элементов И, ИЛИ, НЕ. Обозначения этих элементов на схемах приведены на рис. 5.

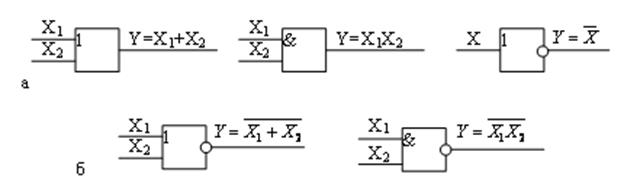
Р и с. 5. Обозначение логических элементов:
а – ИЛИ, И, НЕ; б – ИЛИ–НЕ, И–НЕ

Наибольшее распространение получили элементы, реализующие комбинированные функции И–НЕ, ИЛИ–НЕ (рис. 5, б).

При объединении входов любой из этих элементов реализует функцию НЕ. Для рационального построения комбинационной схемы, реализующей синтезированное выражение логической функции и выполненной на элементах И–НЕ, ИЛИ–НЕ, следует преобразовать полученное выражение с использованием теорем (2) таким образом, чтобы оно содержало максимальное количество операций

, .

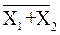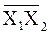Например, выражение (3) может быть преобразовано следующим образом:

.

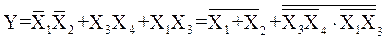Последнее преобразование следует из теоремы

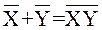или .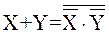

Комбинационная схема, реализующая выражение (3), может иметь вид, представленный на рис. 6.

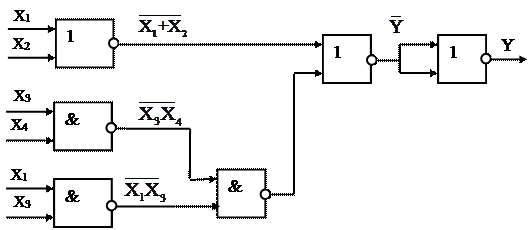
Р и с. 6. Комбинационная схема, реализующая выражение (3)

Триггерные устройства

Одним из наиболее распространенных узлов вычислительных устройств является триггер – схема с двумя устойчивыми состояниями. Триггер имеет два выхода (прямой Q и инверсный ) и несколько информационных входов, при поступлении на которые определенной комбинации сигналов он переходит из одного состояния в другое. Считают, что триггер находится в состоянии “1”, если сигнал на выходе Q соответствует логической “1” (соответственно на выходе – логическому “0”) и, наоборот, в состоянии “0”, если сигнал на выходе Q соответствует логическому “0”.

Триггеры бывают асинхронные (меняющие свое состояние непосредственно при изменении сигналов на информационных входах) и тактируемые, которые могут менять свое состояние только при поступлении на тактовый вход тактирующего сигнала.

Основным типом триггера является триггер SR-типа, имеющий два входа – S (прямой) и R (инверсный). Работа SR-триггера описывается табл. 5.

Таблица 5
Sn	Rn	Qn+1
		X

SR-триггер реализует уравнение

При поступлении в n-й момент времени на входы S, R нулевых сигналов триггер не меняет своего состояния (Q_n+1= Q_n), при поступлении на вход S единичного сигнала триггер устанавливается в единичное состояние, при подаче на вход R единичного сигнала триггер устанавливается в нулевое состояние. Комбинация сигналов R=1, S=1 является запрещенной, при подаче такой комбинации на входы триггер устанавливается в неопределенное состояние X.

Схемы SR-триггера, выполненные на логических элементах, и его обозначение представлены на рис. 7.

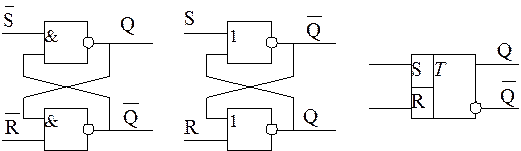
Р и с. 7. Схемы SR-триггера и его обозначение

Тактируемые SR-триггеры имеют на входах схемы для разрешения записи информации. Схемы тактируемого SR-триггера, выполненные на логических элементах, а также его условное изображение представлены на рис. 8.

Тактируемый SR-триггер (SRT-триггер) имеет тактовый вход С.

Триггер D имеет один информационный вход D и устанавливается в состояние, соответствующее информации на этом входе: Q_n+1=D_n.

Наиболее распространены тактируемые D-триггеры. Схемы таких триггеров и их условное изображение представлены на рис. 9.

Счетный триггер имеет счетный вход С и меняет свое состояние каждый раз, как только на счетном входе появляется единичный сигнал С:

Счетный триггер может быть построен на основе тактируемого D-триггера (рис. 10).

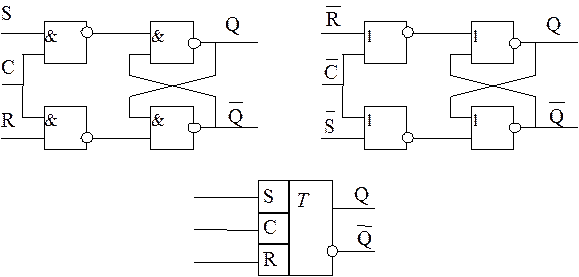
Р и с. 8. Схемы тактируемого SR-триггера и его обозначение

Р и с. 9. Схемы тактируемого D-триггера

.

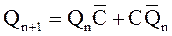Р и с. 10. Схема счетного триггера

Универсальный JK-триггер имеет информационные входы J, K и тактовый вход С. При комбинации сигналов

JK=1,

JK-триггер ведет себя как счетный триггер, т.е. меняет свое состояние на противоположное:

.

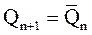При всех других комбинациях сигналов JK-триггер ведет себя аналогично SR-триггеру (J~S, K~R). JK-триггер чаще всего строится по схеме “M-S” (основной-вспомогательный) на основе двух тактируемых SR-триггеров (рис. 11).

При поступлении тактового сигнала на вход С основной триггер “М” воспринимает информацию, подаваемую на входы J, K, затем при поступлении тактового сигнала на вход С₂ вспомогательный триггер “S” фиксирует свое состояние. Часто тактовый сигнал С₂ определяется инверсией тактового сигнала С₁: .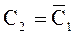

Р и с. 11. JK-триггер, выполненный по схеме “M”-“S”, и его обозначение

При использовании пунктирных связей, изображенных на рис. 11, JK-триггер работает как счетный. Обозначение триггера также приведено на рис. 11.

Дешифраторы и шифраторы

Дешифраторы – схемы, преобразующие код из одного вида в другой, например, двоичный код в десятичный.

Схема такого дешифратора (рис. 12) может быть легко построена на основе комбинационной табл. 6, в которой представлена функция такого преобразования.

Условное обозначение такого дешифратора также изображено на рис. 12.

Таблица 6
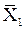
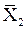
X1	X2			Y

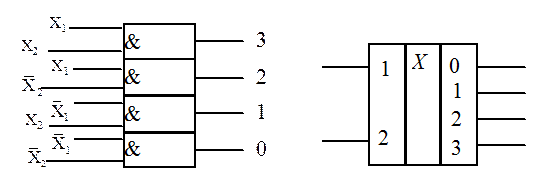
Р и с. 12. Схема и условное обозначение дешифратора,

реализующего функцию табл. 6

Шифратор выполняет функцию, обратную дешифратору, например, преобразует унитарный код в двоичный.

Схема шифратора строится на основе комбинационной таблицы преобразования кодов. Для преобразования кодов, соответствующего табл. 6, схема шифратора может иметь вид, изображенный на рис. 13.

Р и с. 13. Схема шифратора, реализующего функцию в табл. 6

2. Описание лабораторного макета

На лицевой панели лабораторного макета размещены условные изображения 4-х логических двухвходовых схем И–НЕ и 4-х логических двухвходовых схем ИЛИ–НЕ, а также входов и выходов этих схем.

Имеются также выводы постоянных сигналов, соответствующих логическим “0” и “1”.

Макет содержит также формирователь одиночных импульсов, управляемый кнопкой, размещенной в нижней части лицевой панели. Здесь же размещены выводы двухфазного выхода формирователя. В правой части лицевой панели размещены выводы, к которым подключается напряжение питания.

К макету прилагается отдельный блок цифрового коммутатора, в котором имеется генератор прямоугольных импульсов с частотами 100 кГц, 50 кГц, 10 кГц, 5 кГц, 2,5 кГц, а также электронный 8-канальный коммутатор для осциллографа.

50 кГц

t

10 кГц

t

5 кГц

t

2,5 кГц

t

Р и с. 14. Диаграммы сигналов на выходах генератора цифрового коммутатора

Диаграммы сигналов на выходах генератора изображены на рис. 14. Кроме макета и блока коммутатора для выполнения работы требуются:

- источник питания типа ВУЛ-2 – 1 шт.;

- осциллограф типа С1-68 – 1 шт.

3. Порядок выполнения работы

В соответствии с комбинационной таблицей логической функции от 4-x переменных представить соответствующую карту Карно. Вариант комбинационной таблицы выбирается преподавателем из указанных в табл. 7.

В представленной карте Карно выбрать группы, содержащие логическую “1” или логический “0”.

Определить выражение, описывающее соответствующую логическую функцию.

Таблица 7

Х1

Х2

Х3

Х4

Номера вариантов

Преобразовать его с помощью теорем (2) с целью использования в нем как можно большего числа функций

, .

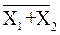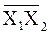В соответствии с выражением логической функции определить реализующую его комбинационную схему.

Дата добавления: 2015-05-26