Собрать схему триггера. 3 страница

На остальные входы микросхемы подать логические сигналы “0”, “1” в соответствии с рекомендациями по применению микросхемы.

Подавая на счетный вход импульсы, контролировать выходной сигнал. Построить экспериментально диаграммы сигналов, сравнить их с теоретическими.

6. Подать на счетный вход микросхемы импульсы частотой 10 кГц.

7. Вход и выход микросхемы соединить с каналами 1 и 2 цифрового коммутатора. Вход синхронизации осциллографа “внеш.” соединить с выходом “P” микросхемы. Остальные соединения между коммутатором, осциллографом и схемой макета выполнить, как было указано в п. 1. режим синхронизации устанавливается как в п. 2.

Сравнить наблюдаемые на экране осциллографа осциллограммы сигналов с осциллограммами, построенными теоретически.

8. Собрать из схем DD1, DD2 шестиразрядный двоичный счетчик. Соединить выход Р схемы DD4 со входом этого счетчика. Выход сигнала переноса Р схемы DD4 через инвертор, выполненной на одной из схем DD5, соединить со входом сброса R счетчика. Выходы счетчика, а также вход Т и выход Р схемы DD4 соединить с каналами 1…8 коммутатора. Наблюдая на экране осциллографа осциллограммы сигналов, полученных с помощью коммутатора, определить код, действующий на выходах счетчика, непосредственно перед появлением импульса на выходе Р. Объясните работу собранной схемы.

Разобрать схему и убрать за собой рабочее место.

4. Содержание отчета

Отсчет должен содержать разработанные схемы счетчиков, регистров, делителей частоты, диаграммы сигналов разработанных схем, описание диаграмм сигналов.

Контрольные вопросы

1. Каковы диаграммы сигналов в схемах D- и JK-триггеров?

2. Каковы диаграммы сигналов в схемах двоичных счетчиков?

3. Как собрать схему счетчика с заданным коэффициентом пересчета?

4. Как работает схема счетчика К155ИЕ7?

5. Как работает схема делителя частоты К155ИЕ8?

6. Как подключить цифровой коммутатор к исследуемой схеме?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Лачин В.И., Савелов Н.С. Электроника: учебное пособие. Изд. 6-е, перераб. и дополн. – Ростов на Д.: Феникс, 2007. – 703 с.

2. Угрюмов Е. Цифровая схемотехника. – СПб.: БХВ, 2001. – 528 с.

3. Валенко В.С. Полупроводниковые приборы и основы схемотехники электронных устройств. – М.: ДОДЭКА-XXI. 2001. – 365 с.

4. Степаненко И.П. Основы микроэлектроники. Изд. 2-е. – М.: Лаборатория Базовых Знаний, 2000. – 488 с.

Лабораторная работа ЭУ-13

“ИССЛЕДОВАНИЕ РЕГИСТРОВ ПАМЯТИ, ДЕШИФРАТОРОВ, МУЛЬТИПЛЕКСОРОВ”

1. Цель работы

Цель работы – ознакомление с характеристиками регистров памяти, дешифраторов, мультиплексоров и применение их в цифровой схемотехнике.

Общие сведения

Регистры памяти, дешифраторы и мультиплексоры выполнены на основе базовых логических элементов в цифровой схемотехнике.

Логические элементы оперируют сигналами, которые могут принимать значения только двух уровней – высокого и низкого (нулевого). Обычно сигнал высокого уровня обозначают единицей “1”, низкого уровня – нулем “0”.

Для описания поведения логических схем используют специальный раздел алгебры – алгебру логики. Все переменные в алгебре логики могут принимать два значения: 0 и 1. наиболее важными функциями алгебры логики являются функции ИЛИ (логического сложения X₁+X₂), И (логического умножения X1·X2), отрицания (инверсии) 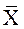(функция НЕ). Эти функции определяются комбинационной табл. 1.

Таблица 1

Х1	Х2	(Х1+Х2)	(Х1Х2)

Функция инверсии является функцией одного аргумента, функции И, ИЛИ могут быть функциями многих аргументов:

Y=X₁X₂...X_n (умножение), Y=X₁+X₂+...+X_n (сложение).

Логическая функция описывается комбинационной таблицей из 2-х строк, двух аргументов – таблицей из 4-х строк, n -аргументов – таблицей из 2 ⁿ строк. Пример – комбинационная табл. 2 для функций Y=X₁X₂X₃ и Y=X₁+X₂+X₃.

Таблица 2

Х1	Х2	Х3	Х1Х2Х3	Х1+Х2+Х3

Cуществуют и другие логические функции. Логическая функция многих аргументов, описывающая реализующую ее комбинационную электронную схему, может определяться не только комбинационной таблицей, но и выражением, включающим в себя определенные выше логические функции, например:

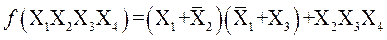. (1)

При подстановке в выражение значений аргументов определяется значение функции, например, при X₁=0, X₂=1, X₃=1, X₄=1 это значение равно

f (0,1,1,1) = (0+ 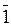) ( 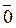+1) + 1·1·1= (0+0) (1+1) + 1·1 = 0·1+1= 0+1 = 1.

Выражение для логической функции можно определить следующим образом, исходя из ее комбинационной таблицы. Для каждого набора переменных, на котором функция равна единице, записывается элементарное произведение всех аргументов, причем если аргумент в этом наборе принимает значение 0, то записывается его инверсия. Выражение для функции определяется логической суммой этих элементарных произведений. Например, функция, заданная в табл. 3, может быть представлена выражением

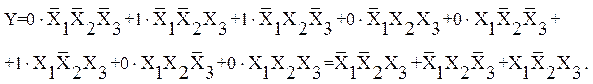(2)

Если функция на всей совокупности наборов переменных принимает нулевое значение меньшее число раз, чем единичное (в столбце комбинационной таблицы число нулей меньше, чем число единиц), то для инверсии функции более компактным выражением будет выражение, составленное аналогичным образом из элементарных произведений аргументов для каждого набора переменных, на котором функция равна нулю. Например, функция, заданная табл. 4, может быть представлена выражением

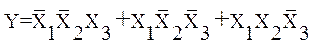(3)

Таблица 3 Таблица 4

Номер набора	Х1	Х2	Х3	Y		Номер набора	Х1	Х2	Х3	Y

Выражения (2) и (3) могут быть приведены к более компактной форме при использовании теорем алгебры логики. Реализуются они с помощью логических элементов И, ИЛИ, НЕ, обозначения которых на схемах приведены на рис. 1.

Распространение получили также элементы, реализующие комбинированные функции И–НЕ, ИЛИ–НЕ. При объединении входов любой из этих элементов реализует функцию НЕ. Комбинационная таблица для этих функций приведена в табл. 5.

Р и с. 1. Обозначение логических элементов

Таблица 5

	Х1	Х2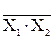

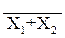
Схема И называется также вентильной, поскольку, как это видно из табл. 1, она пропускает один из сигналов (например, X) на вход (Y = X₁) при значении другого сигнала, равном 1, и не пропускает его (Y = 0) при значении другого сигнала, равном 0.

На основе описанных логических схем строятся основные модули цифровой схемотехники – дешифраторы, мультиплексоры, счетчики, регистры.

Дешифраторы

Дешифратор – это схема для преобразования позиционного двоичного кода в унитарный цифровой код. Он реализует таблицу преобразований, например, для трехразрядного двоичного кода (табл. 6).

Таблица 6

Х1	Х2	Х3	Y
			Y0
			Y1
			Y2
			Y3
			Y4
			Y5
			Y6
			Y7

В этой таблице Y_i – вывод, на котором действует единичный сигнал при соответствующем наборе переменных.

Как видно из табл. 6, дешифратор реализует функции

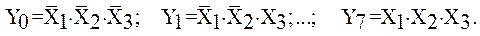
Схема такого дешифратора и его условное изображение представлены на рис. 2.

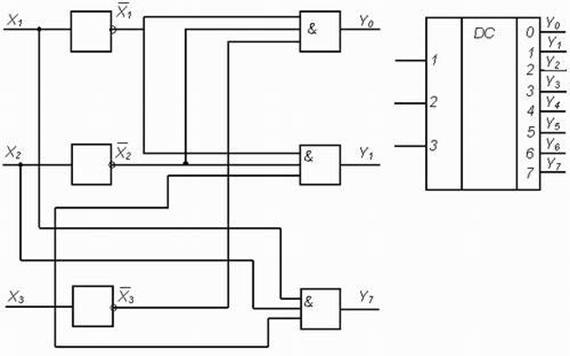
Р и с. 2. Схема дешифратора и его обозначение

Входы 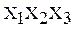называют адресными входами, а сигналы, которые на них поступают, адресными сигналами, или адресами.

Дешифратор используется для реализации произвольной функции алгебры логики. Для этого необходимо использовать схему ИЛИ, входы которой надо соединить с теми выходами дешифратора, на которых действует единичный сигнал при подаче на входы адресов единичных значений логической функции. Например, комбинационная схема, реализующая функцию, заданную табл. 3, изображена на рис. 3. Дешифратор может быть использован также в качестве распределителя сигналов, поскольку при подаче на его входы последовательно увеличивающегося двоичного кода единичный выходной сигнал перемещается в направлении увеличения номера выхода.

Диаграммы сигналов в такой схеме изображены на рис. 4. Двоичный код обычно формируется двоичным счетчиком импульсов C, также изображенных на рис. 4.

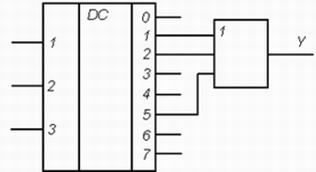
Р и с. 3. Комбинационная схема на дешифраторе

Объединяя выходы распределителя с помощью схем ИЛИ, можно создать схему генераторов различных последовательностей сигналов. Одна из схем двухфазного генератора и диаграмма сигналов приведены на рис. 5.

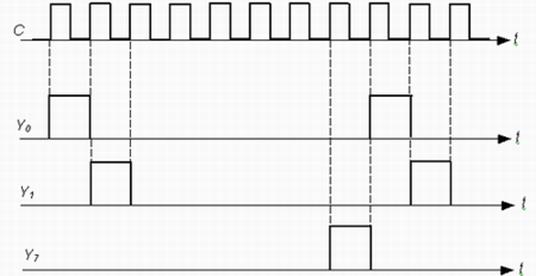
Р и с. 4. Диаграмма сигналов распределителя

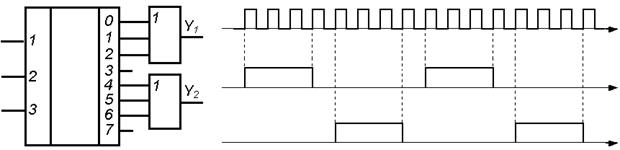
Р и с. 5. Схема двухфазного генератора на основе дешифратора
и диаграммы сигналов

Мультиплексор

Мультиплексор – это схема с одним выходом, информационными и адресными входами. Он передает сигнал на выход с того входа, номер которого определяется адресом – двоичным кодом, действующим на адресных входах. Условное изображение мультиплексора 8 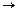1, имеющего информационные входы D₀...D₇, адресные входы 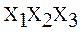и два выхода – прямой Y и инверсный 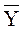, приведено на рис. 6.

Мультиплексор реализует логическую функцию

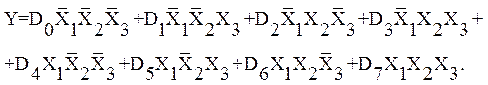(4)

Сравнение выражений (4) и (2) показывает, что мультиплексор можно использовать для реализации логической функции, если входной сигнал D_i рассматривать как конкретное значение Y на соответствующем наборе переменных .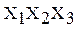

На рис. 7 представлена комбинационная схема, реализующая функцию, заданную в табл. 4.

Р и с. 7. Комбинационная схема на мультиплексоре

Р и с. 6. Мультиплексор

.

Для реализации функции от 4 переменных мультиплексор дополняется инвертором для получения инверсии четвертой переменной X₄. Например, функция Y, описанная в табл. 7, определяется выражением

,

(5)

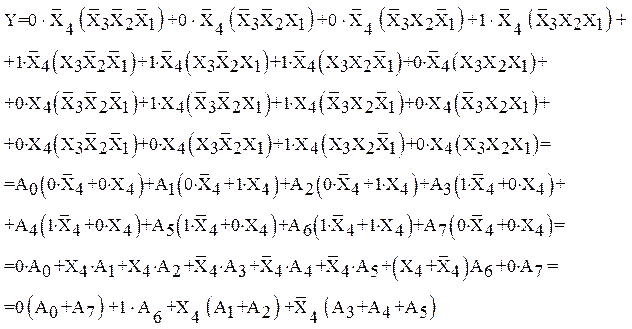
где А_i – переменная, определяемая соответствующим произведением :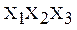

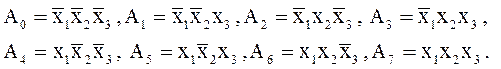
Таблица 7

Номер набора	Х4	Х3	Х2	Х1	Y	Y1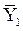

Можно заметить, что i – номер набора 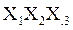, при котором .

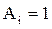Число i определяет и номер входа мультиплексора, на который подается один из сигналов 0,1, в соответствии с выражением (5).

Схема, реализующая эту функцию, изображена на рис. 8, а.

Если функция принимает нулевые значения меньшее число раз, чем единичные, то удобнее составить выражение для инверсии функции, как это было сделано при определении выражения (4), и, соответственно, использовать инверсный выход 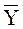мультиплексора. Функция , заданная в правом столбце табл. 8 (отмечен серым цветом), определяется выражением

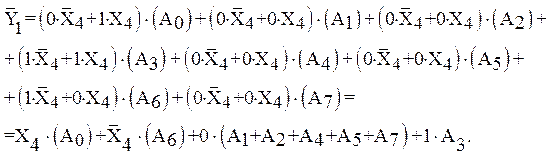
Схема, реализующая эту функцию, изображена на рис. 8, б.

Р и с. 8, а. Комбинационная схема на мультиплексоре

Р и с. 8, б. Комбинационная схема на мультиплексоре с инверсным выходом

Триггерные схемы

Регистры памяти и счетчики строятся на основе триггеров. Триггер – это схема с двумя устойчивыми состояниями, кодируемыми цифрами 0 и 1. Обычно считают, что триггер находится в состоянии 1, если сигнал на его выходе Q имеет высокий уровень (единичный сигнал), и в состоянии 0, если сигнал на его выходе имеет низкий уровень (нулевой сигнал).

Триггер имеет информационный (D) и тактовый (С) входы. При поступлении на информационный вход логического сигнала (“0” или “1”) триггер устанавливается в соответствующее состояние и запоминает его, то есть в триггер записывается информация.

Информация может записываться в триггер только при наличии на тактовом входе единичного сигнала (тактового сигнала, или синхросигнала).

Кроме указанных входов, триггер имеет установочные входы R и S, которые позволяют устанавливать триггер в состояние “0” и “1” путем подачи на эти входы комбинаций сигналов в соответствии с табл. 8. Как видно из таблицы, при нулевых сигналах 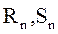триггер не меняет своего состояния .

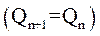Таблица 8

Rn	Sn	Qn+1
		Qn
		x

При других комбинациях триггер устанавливается в состояние, соответствующее сигналу на входе S.

Комбинация сигналов

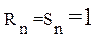
является запрещенной, при ней триггер устанавливается в неопределенное состояние. Триггер может работать в счетном режиме, когда он пересчитывает по модулю 2 импульсы, поступающие на его тактовый вход (счетный вход). Такие счетные триггеры являются основой различных счетчиков.

Счетчики

Счетчики бывают суммирующие, вычитающие и реверсивные, которые могут как суммировать импульсы, так и вычитать. Они характеризуются коэффициентом пересчета К – максимальным количеством сосчитанных импульсов. Коэффициент К зависит от числа разрядов счетчика (каждому разряду соответствует один триггер). Для n -разрядного счетчика максимальное его значение определяется соотношением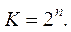

Условное обозначение и диаграммы сигналов суммирующего 4-x разрядного двоичного счетчика представлены на рис. 9.

Можно убедиться, что в интервале времени после i -го входного импульса на выходах счетчика действует двоичный код, соответствующий числу i. Вход R счетчика используется для его сброса в нулевое состояние (очистки). При подаче на R вход логической единицы на выходах счетчика устанавливается нулевой код (0000).

Очевидно, что четырехразрядный счетчик имеет коэффициент пересчета К =2⁴=16.

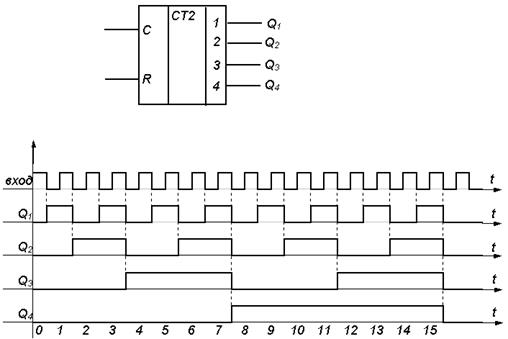
Р и с. 9. Суммирующий двоичный счетчик.
Обозначение и диаграмма напряжений

При поступлении на вход счетчика импульсов частотой f ₀ с выходов 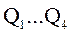снимаются импульсы с частотами 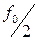, , 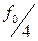, 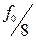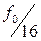(см. рис. 9).

Таким образом, счетчик может быть использован в качестве делителя частоты импульсов в 2, 4, 8 и 16 раз.

Регистры памяти

Регистры памяти также строятся на основе триггеров и служат для запоминания (записи) двоичного кода. Регистр, предназначенный для записи 4-разрядного кода, имеет 4 информационных входа 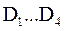, тактовый вход c (синхровход) и четыре выхода 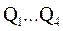(рис. 10).

Р и с. 10. Запоминающий регистр и диаграммы сигналов

После поступления тактового импульса с (синхросигнала) регистр запоминает двоичный код, действующий на входах 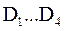непосредственно перед появлением заднего фронта сихросигнала. Информационные сигналы на выходах 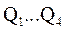регистра появляются в момент заднего фронта синхросигнала.

Регистры сдвига, кроме возможности записи кода, имеют возможность сдвига записанного кода при поступлении тактового импульса на отдельный тактовый вход. При сдвиге кода от младшего разряда к старшему реализуется выражение 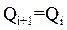. В этом случае в младший разряд записывается информация с отдельного (последовательного) входа .

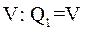В качестве примера можно привести универсальный регистр сдвига К155ИР1, условное изображение которого приведено на рис. 11. Этот регистр имеет два синхровхода С₁ и С₂. Вход V₂ служит для управления режимом работы: при V₂=1 регистр работает в режиме параллельной записи кода, действующего на входах D₁…D₄ при наличии синхроимпульса на c ₁. При этом вход V₁ служит для записи с него информации в младший разряд регистра (Q₁=V₁). При подключении ко входу V₁выхода Q₄ получается кольцевой регистр – код, записанный в него, под действием синхроимпульсов, подаваемых на вход c ₁, циркулирует, последовательно переписываясь с выхода Q₄ на вход V₁, а параллельный код, записанный в регистр, преобразуется в последовательный и может быть считан, например, с выхода Q₄.

Р и с. 11. Универсальный регистр К155ИР1

На основе универсального регистра можно построить различные делители частоты. Для этого входные импульсы необходимо подать на объединенные входы c ₁, c ₂, на вход V₁ подать логическую единицу, вход V₂ соединить с одним из выходов регистра. Схемы делителей с различными коэффициентами деления частоты приведены на рис. 12.

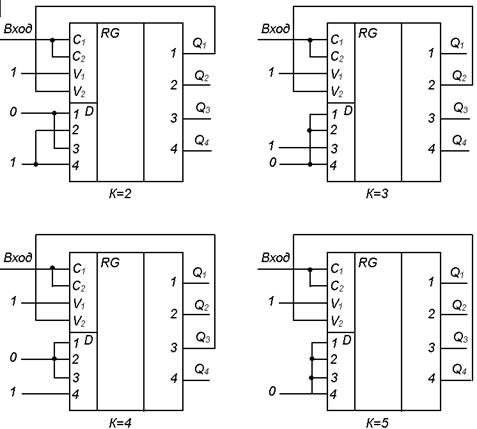
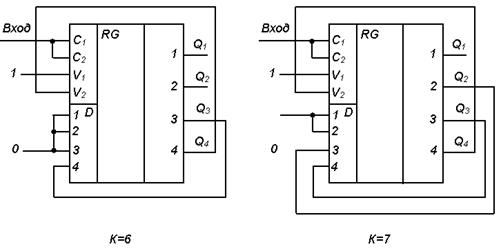
Р и с. 12. Схемы делителей частоты на основе универсального регистра К155ИР1

2. Описание лабораторного стенда

На лицевой панели лабораторного макета имеются условные изображения двоичного счетчика К155ИЕ5, мультиплексора К155КП7, дешифратора К155ДИ3, универсального регистра К155ИР1, двух логических схем И–НЕ и выводы входов и выходов указанных микросхем. Имеются также выводы, на которых постоянно действуют логические сигналы “0” и “1”.

В макете есть два формирователя одиночных импульсов, управляемых кнопками К1 и К2. При нажатии на кнопку К1 на верхнем выводах формирователя действуют сигналы “0” и “1”, при отпущенной кнопке на этих же выводах действуют противоположные сигналы – “1” и “0”.

Аналогичным образом действует формирователь, управляемый кнопкой К2. На панели макета имеются также выводы, к которым подключается напряжение питания 8…10 В.

Микросхема К155ИЕ5 (рис. 13) содержит счетный триггер со счетным входом С₁ и выходом Q₁, трехразрядный двоичный счетчик со входом С₂ и выходами Q₂, Q₃, Q₄, а также входы сброса R ₀, &. При соединении выхода Q₁ со входом С₂ схема представляет собой счетчик с коэффициентом пересчета К=16 и входом С₁.

Р и с. 13. Двоичный счетчик К155ИЕ5

При одновременной подаче единичного сигнала на входы R₀, & счетчик очищается, при подаче нулевого сигнала хотя бы на один из входов R₀, & счетчик работает в режиме счета импульсов. Диаграммы сигналов счетчика изображены на рис. 9.

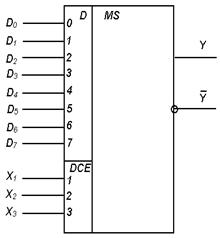
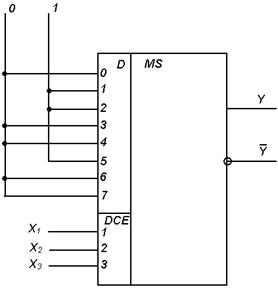
Микросхема К155КП7 (рис. 14) представляет собой мультиплексор 8 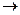1 с информационными входами 0…7, адресными входами DCE 1, 2, 3, синхровходом с. Если на синхровходе логический сигнал равен 1 (с =1), на прямом выходе сигнал Y=0 независимо от значений информационных входных сигналов. Если с =0, то на прямом выходе сигнал повторяет информационный сигнал на том входе, номер которого совпадает с десятичным эквивалентом кода на адресных входах. Например, сигнал на входе Y равен 1 при подаче на входы комбинации сигналов , .

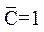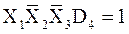Дата добавления: 2015-05-26