Эксперимент Дэвиссона и Джермера

Схема эксперимента была, вкратце, такова. Слаботочный пучок термоэмиссионных электронов направлялся нормально на поверхность среза монокристалла никеля. Монокристалл можно было поворачивать вокруг линии падения пучка, детектор же рассеянных электронов позволял проводить их селекцию по углу рассеяния. Таким образом, имелась возможность сканировать, по отношению к монокристаллу, почти всю заднюю полусферу рассеяния – не затенённую электронной пушкой. Детектор настраивался так, чтобы отсекались электроны с малой энергией и регистрировались только те, которые испытали упругое или почти-упругое рассеяние. Выводы о картинах рассеяния делались на основе величины тока с детектора в зависимости от трёх параметров: энергии падавших электронов и двух углов, определявших направления рассеяния. Следует также обрисовать некоторые важные для нас особенности строения мишени. Никель, как известно, имеет гранецентрированную кубическую решётку. При этом элементарной ячейкой кристалла является куб, содержащий 14 атомов: восемь в вершинах куба и шесть в центрах его граней. Срез монокристалла был выполнен по плоскости {111}, т.е. ортогонально большой диагонали куба. Плоскость {111} имеет плотнейшую упаковку атомов, расположенных в вершинах смежных

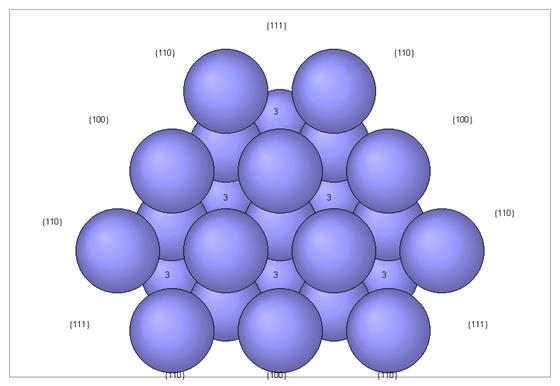
Рис 1.1

равносторонних треугольников. Схематическую картину атомов, какой она видится при прямом взгляде на поверхность идеального среза {111}, мы позаимствовали из [1] (см. рис.1.1). Цифрами 3 помечены атомы третьего слоя; атомы четвёртого слоя расположены точно за атомами первого слоя. Налицо осевая симметрия третьего порядка: при повороте монокристалла по азимуту на угол, кратный 120^о, компоновка атомов в точности повторяется. Азимутальная симметрия третьего порядка наблюдалась и в картинах рассеяния. Воспроизведём схематически ключевые графики из [1] (см. рис.1.2). Показаны две системы пиков – для двух резонансных ускоряющих напряжений и соответствующих им углов рассеяния (между линией падения электронов и направлением на детектор). Два графика размещены на одной диаграмме для удобства сопоставления, их постоянные составляющие в действительности одинаковы. Резонансные пики на этих графиках интерпретируются как результаты брэгговского отражения от систем параллельных атомных плоскостей, которые наклонены к поверхности среза. Судя по данным о компоновке атомов в монокристалле никеля, среди полного набора его атомных плоскостей, наклонённых к поверхности среза {111}, есть системы параллельных плоскостей, во-первых, с углами наклона 26.5^о (в направлениях 111, см. рис.1), и, во-вторых, с углами наклона 21.8^о (в направлениях 100). Соответствующие отражения – на удвоенные углы наклона – должны давать углы рассеяния, почти совпадающие с приведёнными на рис.2. Кроме того, расстояния между плоскостями в вышеназванных системах таковы, что резонансные длины волн (~ 1.5 Ангстрем), рассчитанные для первых порядков брэгговского отражения, с точностью до нескольких процентов совпадают с длинами волн де Бройля при соответствующих ускоряющих напряжениях (расчёт см., например, в [3]). Отсюда делается вывод о том, что рассеяние медленных электронов хорошо объясняется в терминах дифракции волн де Бройля – аналогично тому, как объясняется дифракция рентгеновского излучения с теми же длинами волн. Однако, этот вывод основан на далеко не полной картине происходящего.

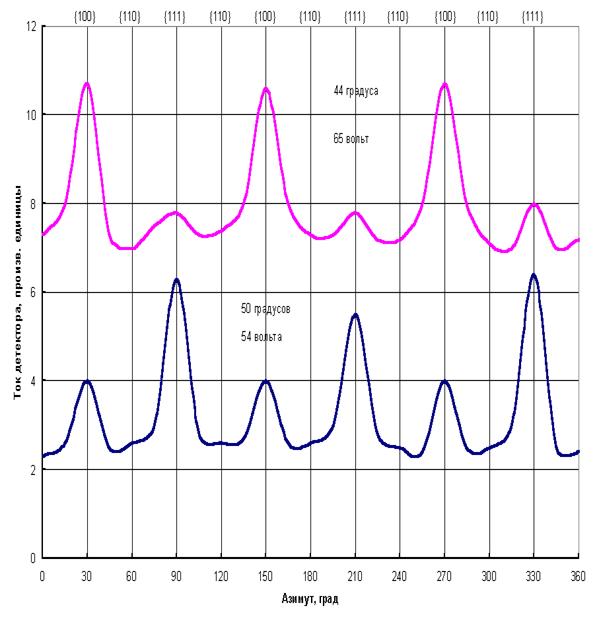Рис.1.2

Дата добавления: 2015-05-29