Показатели вариации и вариационно-дисперсионный анализ

Финансы и кредит

Вариация - различия в значениях того или иного признака у отдельных единиц, входящих в данную совокупность. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Например, успеваемость отдельного студента определяется затратами времени на подготовку к занятиям, способностью к обучению и т.п.

Наличие вариации обусловлено влиянием большого кол-ва факторов на форм-ние уровня признака. Эти ф-ры д-твуют с неодинаковой силой и в разных напр-ниях. Д/описания меры изменчивости признаков исп-т пок-ли вариации. К абсолютным пок-лям относятся размах вариации, ср. линейное отклонение, дисперсия, ср. квадратическое отклонение. К относительным – относительное линейное отклонение, коэффициент вариации.

Размах вариации – разность м/д максимальным и минимальным значениями признака в изучаемой сов-сти. Не дает никакой инф-ии об особенностях иссл-мых сов-стей и не позволяет оценить степень типичности полученных средних. Чтобы дать обобщающую хар-ку распространения отклонений, исп-т ср. линейное отклонение, кот. учитывает различие всех единиц изучаемой сов-сти. Определяется как ср. арифметическое из отклонений индивид. значений от средних без учета знака минус этих отклонений.

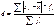
Дисперсия (ср. квадрат отклонений) – ср. арифметическое квадратов отклонений каждого значения признака от общей средней.

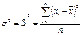
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии. Оно показывает, насколько в среднем колеблется величина признака у единиц иссл-мой сов-сти, и выражается в тех же единицах измерения, что и варианты.

Относительное линейное отклонение хар-т долю усредненного значения абсолютных отклонений от средней величины.

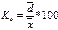
Коэффициент вариации – наиболее часто применяемый пок-ль относительной колеблемости, хар-щий однородность сов-сти.

В основе дисперсионного анализа лежит разделение дисперсии на части или компоненты. При исследовании статистической значимости различия между средними двух (или нескольких) групп сравниваются (анализируются) выборочные дисперсии. Фундаментальная концепция дисперсионного анализа предложена Фишером в 1920 году. Также этот анализ называют анализ суммы квадратов или анализ вариации, но в силу традиции употребляется термин дисперсионный анализ.

Дисперсия (сумма квадратов), основанная на внутригрупповой изменчивости, приводит к гораздо меньшим значениям, чем при вычислении на основе общей изменчивости (относительно общего среднего). Причина этого заключается в существенной разнице между средними значениями, и это различие между средними и объясняет существующее различие между суммами квадратов. Основная логика дисперсионного анализа. Целью дисперсионного анализа является проверка статистической значимости различия между средними (для групп или переменных). Эта проверка проводится с помощью разбиения суммы квадратов на компоненты, т.е. с помощью разбиения общей дисперсии (вариации) на части, одна из которых обусловлена случайной ошибкой (то есть внутригрупповой изменчивостью), а вторая связана с различием средних значений. Последняя компонента дисперсии затем используется для анализа статистической значимости различия между средними значениями. Если это различие значимо, нулевая гипотеза отвергается и принимается альтернативная гипотеза о существовании различия между средними.

Дата добавления: 2015-05-29