Выбор модели

Выбрать модель — значит выбрать вид функции связи реакции с факторами и записать ее уравнение. Тогда останется спланировать и провести эксперимент для оценки численных значений констант (коэффициентов) этого уравнения. Но как выбрать модель? Чтобы ответить на этот вопрос, сначала построим геометрический аналог функции отклика — поверхность отклика. Будем для наглядности рассматривать случай с двумя факторами.

Заметим, что в случае многих факторов геометрическая наглядность теряется. Мы попадаем в абстрактное многомерное пространство, где у нас нет навыка ориентирования. Приходится переходить на язык алгебры. Тем не менее простые примеры, которые мы сейчас рассмотрим, помогут нам при работе со многими факторами. Мы хотим изобразить геометрически возможные состояния «черного ящика» с двумя входами. Для этого достаточно располагать плоскостью с обычной декартовой системой координат.

По одной оси координат будем откладывать в некотором масштабе значения (уровни) одного фактора, а по другой оси — второго (рис. 1.4). Тогда каждому состоянию «ящика» будет соответствовать точка на плоскости. Но, как уже известно, для факторов существуют области определения. Это значит, что у каждого фактора есть минимальное и максимальное возможные значения, между которыми он может изменяться либо непрерывно, либо дискретно. Если факторы совместимы, то границы образуют на плоскости некоторый прямоугольник, внутри которого лежат точки, соответствующие состояниям «черного ящика».

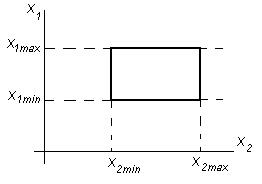
Рисунок 1.4 – Область определения факторов

Пунктирными линиями на рисунке 1.4 обозначены границы областей определения каждого из факторов, а сплошными — границы их совместной области определения.

Чтобы указать значение параметра оптимизации, требуется еще одна ось координат. Если ее построить, то поверхность отклика будет выглядеть так, как на рисунке 1.5.

Пространство, в котором строится поверхность отклика, мы будем называть факторным пространством. Оно задается координатными осями, по которым откладываются значения факторов и параметра оптимизации.

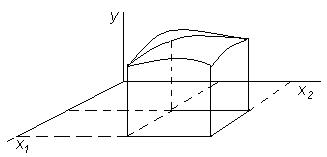
Рисунок 1.5 – Поверхность отклика

Размерность факторного пространства зависит от числа факторов. При многих факторах поверхность отклика уже нельзя изобразить наглядно и приходится ограничиваться только алгебраическим языком. Но для двух факторов можно даже не переходить к трехмерному пространству, а ограничиться плоскостью. Для этого достаточно произвести сечение поверхности отклика плоскостями, параллельными плоскости X10X2, и полученные в сечениях линии спроектировать на эту плоскость.

Так строят, например, изображения гор и морских впадин на географических картах рисунок 1.6. Точка М на рисунке — это и есть та оптимальная точка, которую мы ищем. Каждая линия соответствует постоянному значению параметра оптимизации. Такая линия называется линией равного отклика.

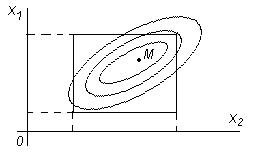
Рисунок 1.6 – Проекция сечений поверхности отклика на плоскость

Существует соответствие между состоянием «ящика» и значением параметра оптимизации: каждому возможному состоянию «ящика» соответствует одно значение параметра оптимизации. Однако обратное неверно: одному возможному значению параметра оптимизации может соответствовать и одно, и несколько состояний «ящика». Правда, эти утверждения справедливы, если не учитывать ошибок в определении значений параметра оптимизации.

К вопросу об оценке и учете этих ошибок мы вернемся ниже, а пока не будем принимать их во внимание. Теперь, когда можно представить себе поверхность отклика, пора вернуться к основному вопросу: как ставить эксперимент, чтобы найти оптимум при минимуме затрат? Это, прежде всего вопрос стратегии. Если бы мы располагали таблицей, в которой содержались бы все возможные состояния объекта и соответствующие им отклики, то особой необходимости в построении математической модели не было бы. Просто мы бы выбрали то (или те) состояние, которое соответствует наилучшему отклику. Но мы уже знаем, сколь велик перебор возможных состояний, и должны отказаться от практической реализации этой возможности.

Другая возможность — случайный выбор некоторого числа состояний и определение откликов в них, в надежде, что среди этих состояний попадется оптимальное состояние или, по крайней мере, близкое к нему. Мы не будем рассматривать эту интересную возможность, так как, к сожалению, она не вписывается в нашу тему [1].

Наконец, третья возможность — строить математическую модель, чтобы с ее помощью предсказывать значения откликов в тех состояниях, которые не изучались экспериментально. Если не можем измерить отклик в каждом состоянии, то сумеем хоть предсказывать результат. Причем даже не в каждом состоянии, а только в наиболее интересных, в тех, которые приближают нас к оптимуму.

Такая стратегия приводит нас к шаговому принципу, лежащему в основе рассматриваемого метода планирования эксперимента [2, 3].

Шаговый принцип. За отказ от полного перебора состояний надо чем-то платить. Цена — это предположения, которые мы должны сделать относительно свойств неизвестной нам модели до начала эксперимента (как говорят, априори).

Некоторые из предположений мы никогда не сможем проветрить. Такие предположения называются постулатами. Если в действительности они не выполняются, то весьма возможно, что мы не найдем оптимум. Точнее, мы примем за оптимум то, что на самом деле им не является (хотя, быть может, нас и удовлетворит). Какие же предположения о свойствах поверхности отклика мы делаем?

Главное — это непрерывность поверхности, ее гладкость и наличие единственного оптимума (быть может, и на границе области определения факторов).

Эти постулаты позволяют представить изучаемую функцию в виде степенного ряда в окрестности любой возможной точки факторного пространства (такие функции в математике называются аналитическими). Кроме того, если мы найдем какой-то способ постепенного приближения к оптимальной точке, нужно, чтобы результат не зависел от исходной точки. Если оптимум один, то неважно, приближаемся мы к нему справа или слева,

а если их несколько, да они еще неравноценны.

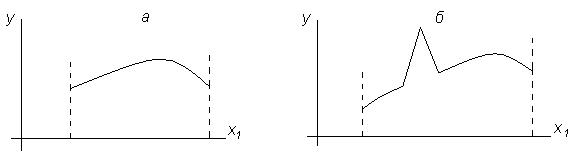
Рисунок 1.7 – Примеры функций отклика для одного фактора

На рисунке 1.7 приведены две картинки, изображающие функции отклика для одного фактора. На рисунке 1.7а показан благоприятный случай. На рисунке 1.7б — много нарушений. Здесь и два экстремума (оптимума) и пик (нарушение гладкости и непрерывности). Если в поисках оптимума мы начнем последовательно двигаться слева направо, то найдем наименьший из максимумов и вряд ли узнаем о существовании второго, наибольшего. Правда, он так локализован и остер, что его не мудрено пропустить и при движении с правого конца, если ставить опыты не во всех точках. Возможно, вы обратили внимание на то, что требование непрерывности не согласуется с представлением о дискретных уровнях факторов.

Однако в действительности это не страшно. Мы ведь можем считать, что фактор принимает непрерывный ряд значений (если даже некоторые значения не имеют смысла или физически нереализуемы). Важно только помнить о таком соглашении при использовании результатов.

А для построения математической модели это создает значительные удобства. Так как мы заранее считаем, что предпосылки выполняются, то надо максимально использовать возможности, которые при этом открываются. Если, например, мы будем знать значения параметра оптимизации в нескольких соседних точках факторного пространства, мы сможем (в силу гладкости и непрерывности функции отклика) представить себе результаты, которые можно ожидать в других соседних точках.

Следовательно, можно найти такие точки, для которых ожидается наибольшее увеличение (или уменьшение, если мы ищем минимум) параметра оптимизации. Тогда ясно, что следующий эксперимент надо переносить именно в эти точки. Надо продвигаться в этом направлении, пренебрегая остальными (Вот где экономятся опыты!).

Сделав новый эксперимент, снова можно оценить направление, в котором скорее всего следует двигаться. В силу единственности оптимума мы, таким образом, рано или поздно непременно его достигнем. Это и есть шаговый принцип. Сделаем некоторые пояснения. Мы выбираем в факторном пространстве какую-то точку и рассматриваем множество точек в ее окрестности, т. е. выбираем в области определения факторов малую подобласть. Здесь мы хотим провести эксперимент, на основании которого должна быть построена первая модель.

Эту модель мы намерены использовать для предсказания результатов опытов в тех точках, которые не входили в эксперимент. Если эти точки лежат внутри нашей подобласти, то такое предсказание называется интерполяцией, а если вне — экстраполяцией. Чем дальше от области эксперимента лежит точка, для которой мы хотим предсказать результат, тем с меньшей уверенностью это можно делать. Поэтому мы вынуждены экстраполировать недалеко и использовать результаты экстраполяции для выбора условий проведения следующего эксперимента.

Дальше цикл повторяется. Попутно полученную модель можно использовать для проверки различных гипотез о механизме изучаемого явления или о его отдельных сторонах. Например, если вы предполагаете, что увеличение значения некоторого фактора должно приводить к увеличению значения параметра оптимизации, то с помощью модели можно узнать, так ли это. Такая проверка называется интерпретацией модели. Она, конечно, имеет большое значение, и мы вернемся к ней позже.

Рисунок 1.8 – Два способа поиска оптимума

На рисунке 1.8 изображены два варианта поиска оптимума для одной и той же поверхности. Крестиками на рисунке обозначены условия опытов. Для случая «а» использован подход, который иногда называют классическим (метод Гаусса—Зейделя). Он состоит в том, что сначала последовательно изменяются значения одного фактора. (На рисунке этот эксперимент обозначен 1.)

Затем находится и фиксируется наилучшее значение этого фактора. В этих условиях последовательно изменяются значения второго фактора и т. д. (если больше факторов).

В случае «б» представлен простейший вариант шаговой процедуры. Сначала изучается локальная область A, затем определяется наиболее интересное направление и в этом направлении ставятся следующие опыты B). Оказалось (см. рисунок 1.8), что в обоих случаях достигнут одинаковый результат при одинаковом суммарном количестве опытов. Как вы думаете, всегда ли эти две процедуры эквивалентны? Что нам требуется? Выяснить, нет ли нарушений наших предпосылок.

Легче всего установить, сколько оптимумов (экстремумов) имеет изображенная функция. Если экстремумов больше одного, то уже нарушена предпосылка. Кроме того, существенно, нет ли каких-нибудь нарушений гладкости и непрерывности функции (например, пиков).

Дело в том, что эффективность зависит от вида поверхности, а также от того, в какой последовательности перебираются факторы в случае а, и из окрестностей какой точки начат эксперимент в случае б.

Попробуйте вместо окружностей, которые задают линии равных откликов, нарисовать эллипсы, главные оси которых составляют некоторый острый угол с осями координат. Вы увидите, что эффективность процедур окажется различной.

Вот иллюстрация, которая сразу показывает правильность вашего ответа (рисунок 1.9). Это, разумеется, только иллюстрация. В жизни не всегда удается за один цикл достигнуть оптимума.

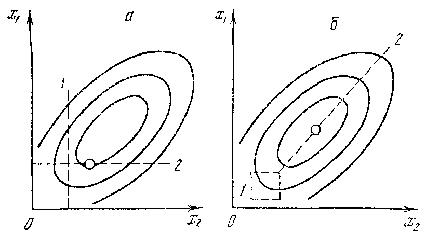
Рисунок 1.9 – Два способа поиска оптимума

Но несомненно, что, по крайней мере, в отношении результата процедура б, т. е. шаговый метод, в среднем эффективнее, чем процедура а. Можно придумать и более конкурентно-способные процедуры, чем а, но они обычно требуют значительно больше опытов. Теперь займемся выбором модели для первого эксперимента более конкретно.

Как выбрать модель? Модели бывают разные. Моделей бывает много. Чтобы выбрать одну из них, надо понять, что мы хотим от модели, какие требования мы к ней предъявляем.

Теперь мы, пожалуй, сможем сформулировать эти требования. Исходя из выбранной стратегии, ясно, что главное требование к модели — это способность предсказывать направление дальнейших опытов, причем предсказывать с требуемой точностью. Так как до получения модели мы не знаем, какое направление нам понадобится, то естественно требовать, чтобы точность предсказания во всех возможных направлениях была одинакова.

Это значит, что в некоторой подобласти, в которую входят и координаты выполненных опытов, и, предсказанное с помощью модели, значение отклика не должно отличаться от фактического больше, чем на некоторую заранее заданную величину.

Модель, которая удовлетворяет такому или какому-либо аналогичному требованию, называется адекватной. Проверка выполнимости этого требования называется проверкой адекватности модели. Разработаны специальные статистические методы, с помощью которых проверяется адекватность.

Мы их рассмотрим ниже. Если несколько различных моделей отвечают нужным требованиям, то следует предпочесть ту из них, которая является самой простой. На рисунке 1.10 изображена логарифмическая функция.

Рисунок 1.10 – График логарифмической функции

На некотором отрезке 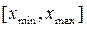она с удовлетворительной точностью описывается двумя уравнениями:

В уравнении B) b — коэффициент, который мы можем оценить, например, по результатам эксперимента. Какое из уравнений, A) или B), по вашему мнению, проще? Простота — вещь относительная.

Если вы заранее не сформулируете точно, что называется простым, а что сложным, то невозможно произвести выбор. На будущее мы договоримся, что при прочих равных условиях мы всегда будем предпочитать степенные ряды. Точнее, отрезки степенных рядов — алгебраические полиномы. При таком соглашении можно сказать, что уравнение B) проще, чем уравнение A).

Фактически мы произвели выбор класса моделей. Мы сказали, что всегда, когда возможно, будем искать модель среди полиномов. Построение полинома возможно в окрестностях любой точки факторного пространства, поскольку мы предположили, что функция является аналитической. Выбрать — значит сравнить.

А как сравнить между собой классы моделей, если свойства объекта заранее неизвестны? Остается предполагать, что нам будут редко встречаться задачи, в которых исходные постулаты окажутся неверными. Если это так, то мы действительно выбрали наиболее простой, удобный и математически разработанный класс моделей. Возможно, что кто-то заранее выбрал для нашей задачи конкретную модель. Тогда тоже возникает необходимость в планировании эксперимента для оценки ее коэффициентов. Но мы не будем рассматривать задачи этого типа.

Давайте выпишем полиномы для случая двух факторов. Они будут различаться по максимальным степеням входящих в них переменных.

Полином нулевой степени: .

Полином первой степени: .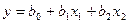

Полином второй степени: .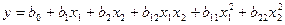

Полином третьей степени:

.

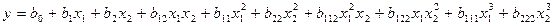Полиномиальные модели. Итак, мы представили неизвестную нам функцию отклика полиномом. Операция замены одной функции другой, в каком-то смысле эквивалентной функцией называется аппроксимацией. Значит, мы аппроксимировали неизвестную функцию полиномом. Но полиномы бывают разных степеней. Какой из них взять на первом шаге?

Эксперимент нужен только для того, чтобы найти численные значения коэффициентов полинома. Поэтому чем больше коэффициентов, тем больше опытов окажется необходимым. А мы стремимся сократить их число. Значит, надо найти такой полином, который содержит как можно меньше коэффициентов, но удовлетворяет требованиям, предъявленным к модели. Чем ниже степень полинома при заданном числе факторов, тем меньше в нем коэффициентов.

Мы хотим, чтобы модель хорошо предсказывала направление наискорейшего улучшения параметра оптимизации. Такое направление называется направлением градиента. Ясно, что движение в этом направлении приведет к успеху быстрее, чем движение в любом другом направлении (это значит, что будет достигнута экономия числа опытов). Как вы думаете, можно ли в этой связи всегда использовать полином первой степени?

С одной стороны, он содержит информацию о направлении градиента, с другой — в нем минимально возможное число коэффициентов при данном числе факторов. Единственное опасение в том, что неясно, будет ли линейная модель всегда адекватной. Ответ зависит еще и от объекта. Этим нам и предстоит сейчас заняться, чтобы завершить этот раздел.

Вопрос в том, как выбрать подобласть в факторном пространстве, чтобы линейная модель оказалась адекватной. Условие аналитичности функции отклика гарантирует нам эту возможность. Всегда существует такая окрестность любой точки (точнее, почти любой точки), в которой линейная модель адекватна. Размер такой области заранее не известен, но адекватность, как вы помните, можно проверять по результатам эксперимента.

Значит, выбрав сначала произвольную подобласть, мы, рано или поздно, найдем ее требуемые размеры. И как только это случится, воспользуемся движением по градиенту. На следующем этапе мы будем искать линейную модель уже в другой подобласти. Цикл повторяется до тех пор, пока движение по градиенту не перестанет давать эффект. Это значит, что мы попали в область, близкую к оптимуму. Такая область называется «почти стационарной». Здесь линейная модель уже не нужна. Либо попаданием в почти стационарную область задача решена, либо надо переходить к полиномам более высоких степеней, например второй степени, чтобы подробнее описать область оптимума.

Удачный выбор подобласти имеет, как вы видите, большое значение для успеха всей работы. Он связан с интуитивными решениями, которые принимает экспериментатор на каждом этапе. Как это делается, мы рассмотрим ниже.

Кроме задачи оптимизации, иногда возникает задача построения интерполяционной модели. В этом случае нас не интересует оптимум. Просто мы хотим предсказывать результат с требуемой точностью во всех точках некоторой заранее заданной области. Тут не приходится выбирать подобласть. Необходимо последовательно увеличивать степень полинома до тех пор, пока модель не окажется адекватной. Если адекватной оказывается линейная, или неполная квадратная модель (без членов, содержащих квадраты факторов), то ее построение аналогично тому, что требуется для оптимизации.

Дата добавления: 2015-05-26