Использование ППП Eureka и Excel при решении задач оптимизации

Метод золотого сечения

Золотое сечение проводит деление отрезка АВ на две неравные части так, чтобы было справедливо соотношение (рис. 7).

Рис. 7

Метод золотого сечения позволяет сужать отрезок [a, b] каждый раз вычисляя лишь одно значение F(x), а не два, как в методе дихотомии.

Данный метод реализуется следующим алгоритмом:

1. Находим коэффициент дробления k=(√5-1)/2 отрезка [a, b].

2. Находим абсциссу х₁=a + (1-k)*(b-a) и вычисляем F(x₁).

3. Находим абсциссу х₂=a + k*(b-a) и вычисляем F(х₂).

4. Проверяем выполнение условия |x₂-x₁|<E, где E – заданная погрешность вычисления x_n. Если это условие выполняется, вычисляем x_n = (x₁+ x₂)/2 и F(x_n), после чего останавливаем счёт с выдачей значений x_m и F(x_n). Если данное условие не выполняется, идём к п.5.

5. Проверяем условие F(x₁) < F(x₂). Если оно выполняется, полагаем, а = х₁, х₁ = х₂ и F(x₁) = F(x₂), после чего идём к п.3. и п.4.

Если F(x₁) ≥ F(x₂), полагаем b = x₂, x₂ = x₁, f(x₁) = f(x₂), после чего выполняем п.2 и п.4

Использование ППП Eureka для поиска экстремумов функций одной переменной.

Для поиска максимумов функций одной переменной необходимо в окне Edit набрать

$|__|max(F)

y(x)=

F=y(x)

В окне Solution будет выдано решение

F=

x=

Перед решением задачи весьма полезно оценить вид функции, экстремум которой необходимо найти и уточнить интервал x, в котором этот экстремум находится. Для этого достаточно воспользоваться командой Plot в позиции Graf основного меню. Из вида графика сделать вывод о правильности решения.

Использование ППП Excel для поиска экстремумов функций одной переменной.

Для поиска максимумов функций одной переменной необходимо:

Вызвать Подбор параметра, с помощью команды в меню Сервис. Окно Подбор параметра состоит из трех полей:

- Установить целевую ячейку, в котором ставится ссылка на ячейку с формулой (Y);

- Равной – выбираем максимальному значению;

- Изменяя ячейки, в которой ставится ссылка на ячейку с изменяемым параметром (первая граница, а интервала (а,в)).

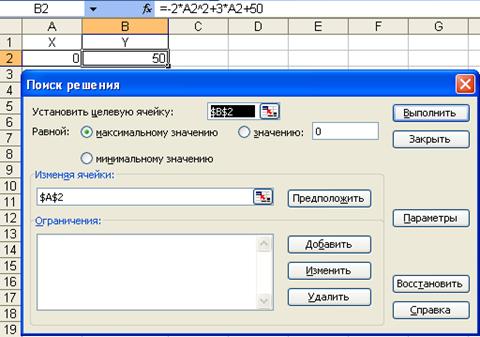
После нажатия кнопки OK, появляется окно, Результаты поиска решения, сохраняем найденное решение. Полученное решение:

Содержание отчета

1. Содержательная постановка задачи.

2. Исходные данные.

3. Краткое описание методов.

4. Блок схема подпрограмм и блок схема головного (или управляющего) модуля.

5. Листинг подпрограмм и управляющего модуля.

6. Распечатка полученных результатов.

7. Распечатка результатов в Excel и Эврика.

Дата добавления: 2015-05-29