Перспективный масштаб на фронтальной, вертикальной и прямой широт. Решение прямой и обратной задачи. Приведите примеры. 2 страница

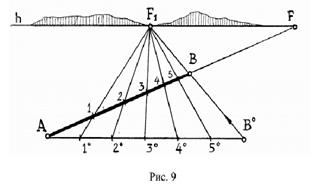
частей (например, шесть) произвольного размера. Через последнюю точку В

делительного масштаба и точку В перспективы отрезка АВ проводят прямую

до пересечения с линией горизонта h и отмечают точку F1. Это точка схода

перспектив горизонтальных прямых, параллельных прямой ВВ0

. Через точку

схода F1

и точки 1

, 2

,.., 5

делительного масштаба проводят прямые и от-

мечают точки их пересечения 1, 2, 3, 4, 5 с перспективой отрезка АВ, кото-

рые разделили AB на шесть перспективно равных частей.

При делении АВ на пропорциональные части, находящиеся в заданном

отношении l: т: n:..., делят масштаб на пропорциональные части произ-

Рис. 8 11

вольного размера, находящиеся друг к другу в том же отношении

l: т: n: …. Дальнейшие построения аналогичны рассмотренному выше

примеру (рис. 10).

На рис. 11 показано построение деления перспективы отрезка АВ пря-

мой общего положения. Указанные ранее действия можно выполнить с вто-

ричной проекцией А1

В1 этого отрезка. Полученные точки переносят на пер-

спективу отрезка АВвертикальными прямыми. 12

Другой вариант пропорционального деления отрезка прямой общего

положения требует нахождения точки схода F1 этой прямой, что показано на

рис. 12. Через точку схода F1

данной прямой АВ проводят произвольную

прямую (на чертеже – горизонтальную). Данную пропорцию откладывают на

прямой АВ0

, параллельной предыдущей прямой, проведенной через точку F1.

Конечную точку В

соединяют с точкой В и находят точку F2. Остальное по-

строение аналогично предыдущим примерам и видно из чертежа.

8. Перспективный масштаб на глубинной прямой. Дробное дистанционное расстояние. Масштабная шкала. Процесс построения данного масштаба на проецирующем аппарате и на картине. Решение прямой и обратной задачи.

Масштаб, построенный на прямой, перпендикулярной к плоскости картины, называется масштабом глубин. Рассмотрим его построение на проецирующем аппарате (рис. 90, а). Сначала задают в предметной плоскости глубинную прямую АоА8. Она перпендикулярна к плоскости картины. На основании картины от точки Ао отмечают делениями 1о, 2о, 3о натуральные отрезки в масштабе картины. Затем переносят (откладывают циркулем) эти отрезки с основания картины на заданную прямую АоА8 и соединяют одноименные точки параллельными прямыми 1о-1', 2о-2', Зо-3'. На рисунке 90, б показано геометрическое построение. Эпоха Возрождения
Заметим, что треугольники 1оАо1', 2оАо2', 3оАо3' прямоугольные, равнобедренные (катеты равны по построению) и подобные (параллельны сходственные стороны).
Далее находят перспективное изображение глубинной прямой и пучка параллельных прямых. Перспективой заданной прямой будет отрезок А0Р, так как предельной точкой глубинной прямой является главная точка. Перспективу параллельных прямых строят при помощи их общей предельной точки. Направив луч зрения SD параллельно данным прямым, находят точку его пересечения с линией горизонта. Точка D будет точкой схода пучка параллельных прямых. Тогда линии переноса 1о-D, 2"-D, 3"-D в пересечении с прямой АоР отметят точки 1, 2, 3, которые определят перспективные отрезки Ао-1, 1-2, 2-3, равные по длине отрезкам, заданным на основании картины!
Рассмотрим образовавшийся в плоскости горизонта треугольник SPD. Он подобен треугольнику 1оАо1', так как у них параллельны сходственные стороны. Следовательно, он прямоугольный и равнобедренный, а катеты SP и PD равны между собой. Отсюда следует, что при построении масштаба глубин точкой схода линий переноса является дистанционная точка, которая находится на линии горизонта и отстоит от главной точки Р на зрительное расстояние SP. Выполнение графических работ Построение аксонометрических изображений Начертательная геометрия

Рис. 90
Как видим, построение масштаба глубин связано с положением точки зрения относительно картины. При построении перспективных изображений дистанционное расстояние является одним из элементов картины и задается автором-художником.
Линии переноса, составляющие с основанием картины угол 45°проводят на предметной плоскости в двух различных направлениях.

Поэтому на линии горизонта отмечают две дистанционные точки
D1 и D2, расположенные по разные стороны и на равном расстоянии от главной точки Р (рис. 90, в). Если прямая находится слева от линии главного вертикала, то пользуются левой дистанционной точкой Dx (рис. 91, а), а если прямая справа, то применяют точку D2
Для построения перспективного масштаба глубин натуральный масштаб, заданный на основании картины, переносят на глубинную прямую с помощью линий переноса, имеющих точку схода дистанционную.
Если нужно построить в перспективном масштабе на глубинной прямой отрезок от заданной точки А, то через нее и дистанционную точку проводят линию переноса до пересечения с основанием картины. От полученной точки Ао на основании картины откладывают натуральную единицу масштаба (например, АоВо - - 1 м) и проводят вторую линию переноса, которая отметит на заданной прямой точку В, ограничивающую отрезок АВ, равный 1 м-в масштабе картины.
Для определения натуральной величины глубинного отрезка, изображенного на картине, проводят через его концы и дистанционную точку линии переноса до пересечения с основанием картины.

Рис 91

Занесенная величина в соответствии с натуральным масштабом картины определит размер отрезка.
На рисунке заданный отрезок АВ составляет 2,5 м в масштабе данной картины.
Дробная дистанционная точка. В практике построения перспективных изображений зрительное дистанционное расстояние часто значительно превосходит линейные размеры картины, вследствие чего дистанционная точка выходит за ее пределы. Чтобы перспек-втивное изображение предмета соответствовало зрительному впечат-[лению, расстояние точки зрения от картины должно быть равно (1,5-2 диаметрам поля ясного зрения человека (см. § 4). При этом расстоянии дистанционная точка и выходит за пределы картины, что осложняет построение и делает его менее точным. В таких случаях тя построения масштаба глубин пользуются так называемой дробой дистанционной точкой.
Рассмотрим применение дробной дистанционной точки. На картине дана глубинная прямая АоР и при помощи дистанционной точки D построен перспективный отрезок АоВ = а. Заметим, этот же отрезок можно построить на картине, если соединить середину отрезка натурального масштаба делящей пополам дистанционное расстояние PD.

Рис 92
Если для построения масштаба глубин нельзя воспользоваться полным дистанционным расстоянием, то задают некоторую его часть, находящуюся в пределах картины. Отметив соответствующую
дробную дистанционную точку на линии горизонта, ее используют как точку схода линий переноса для делений натурального масштаба, единица которого составляет эту же часть единицы заданного масштаба.
Заметим, что на картине (рис. 92, б) при дробной дистанционной точке получают перспективный масштаб глубин, единица которого соответствует полной единице первоначально заданного натурального масштаба. При таком построении каждое деление полного натурального масштаба при переносе на перспективный масштаб отмечает отрезок, соответствующий п единицам натурального.

9. Окружность в перспективе. Способ описанного квадрата (по 8 и 16 точкам). Построение окружности, расположенной в плоскостях наклонных к предметной плоскости.

Существует несколько способов построения, наиболее простой из

них – построение отдельных точек этой окружности (восемь), вписанной в

квадрат.

Предварительно строится квадрат с осями и диагоналями, затем опре-

деляются восемь точек: четыре точки (1, 2, 3, 4) касания к сторонам квадрата

и четыре точки (5, 6, 7, 8) пересечения окружности с диагоналями квадрата

(рис. 14). В перспективе для нахождения четырех точек на диагоналях квад- рата можно использовать простое построение, применяемое в техническом

рисунке:

1) точки 1, 2, 3, 4 – пересечение осей со сторонами квадрата;

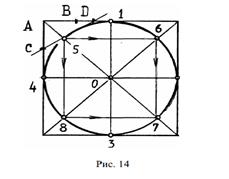
2) при вершине A квадрата с помощью дополнительных диагоналей

делят пополам половины смежных сторон, получают точки Ви С;

3) отрезокB-1 делят такимже образом пополам и получают точку D;

4) соединяют С и D, прямая CD в пересечении с диагональю квадрата

даст точку 5;

5) параллельным переносом находят положение остальных точек на

диагоналях квадрата (6, 7 и 8);

6) плавно соединяют восемь точек, на ортогональном изображении

(рис. 14) получается окружность, в аксонометрии и в перспективе – эллипс.

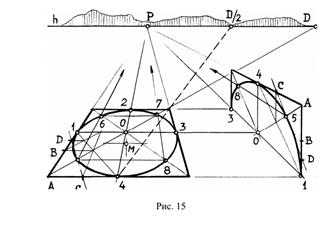
Построение перспективы окружности в горизонтальной плоскости по-

казано на рис. 15.

Построению перспективы окружности предшествует создание перспек-

тивы квадрата. Если две стороны квадрата параллельны основанию картины,

используют дистанционную точку D. Если дистанционная точка окажется за

пределами чертежа, можно воспользоваться дробной дистанционной точкой

D/2, проведя перспективу диагонали полуквадрата – прямую 4-D/2 (штрихо-

вая линия).

После построения перспективы квадрата определяют его центр пересе-

чением диагоналей и проводят оси, одна из которых на чертеже параллельна

горизонту, а другая имеет своей точкой схода точку P на линии горизонта.

Оси квадрата в пересечении со сторонами дали точки 1, 2, 3, 4.

Построение точек 5, 6, 7, 8 производят рассмотренным выше способом.

При вычерчивании кривой эллипса в перспективе необходимо иметь в

виду, что точка O – перспектива центра (точка пересечения диагоналей квад-

рата) и точка M – геометрический центр эллипса не совпадают.

Построение перспективы окружности в вертикальной плоскости анало-

гично, что видно из чертежа.

Примеры построения перспективы с использованием делительного

масштаба, вписыванием окружности и других операций даны на рис. 16, 17

и 18.

10. Построение теней в перспективе. Различные случаи положения солнца и построение солнечных теней от предметов и их элементов (прямой, плоскости и др.). Преломление теней. Приведите примеры.

В природе существуют два естественных источника освеще­ния — Солнце и Луна. При естественном освещении источник све­та находится в бесконечности, поэтому световые лучи принимают за параллельные. Особенностью солнечного и лунного освещения является постоянное движение светил. В связи с этим очертание падающей тени от изображаемых объектов постоянно меняется,

в отличие от искусственного источника света, при котором они остаются неподвижными.

При солнечном освещении, как и при точечном, на основе выб­ранного направления солнечных лучей на картине задают светящу­юся точку и ее проекцию — это обязательное условие для построе­ния теней от предметов. Поэтому сначала надо установить положение Солнца относительно зрителя. Оно может находиться перед рисую­щим, сзади или сбоку от него. Как же строят тени от предметов при различном положении солнца? Рассмотрим примеры.

Солнце находится перед зрителем. В этом случае солнечные лучи являются восходящими параллельными прямыми общего (или особого) положения. На основе законов перспективы известно, что восходящие параллельные прямые имеют точку схода над линией горизонта, а их проекции — на горизонте.

Следовательно, если Солнце находится точно перед зрителем, то оно расположено на линии главного вертикала, а его проекция совпадает с главной точкой. При таком положении Солнца парал­лельные лучи являются прямыми особого положения (илл. 252,а). В этом случае предмет обращен к зрителю своей теневой стороной, и его изображение на картине воспринимается силуэтным, а тени, увеличиваясь по ширине, направлены на зрителя

Обратим внимание, что тень от призмы построена по одной вершине (А,). Поскольку ребра верхнего основания и тень от них на горизонтальную плоскость между собой параллельны, то они имеют общие точки схода (F_t и F₂). Тень от цилиндра построена по центру (О) и диаметру (BE) верхнего основания с применением способа описанного квадрата.

Если Солнце находится перед зрителем и от линии главного вертикала оно смещено вправо или влево, то тень от предмета на­правлена в противоположную сторону от источника света. Пред­

мет обращен к зрителю также теневой стороной. При таком поло­жении солнца параллельные лучи являются восходящими прямы­ми общего положения (илл. 252,6).

Для построения тени от конуса достаточно построить тень от его вершины (А*) и провести касательные к основанию. Тень от призмы построена по одной вершине и с применением дистанци­онных точек схода для горизонтальных ребер верхнего основания.

При расположении Солнца перед зрителем освещение будет контражурным. В этом случае изображаемые объекты выгл ядя т си- луэтно и при восприятии теряется ощущение их объемности. Вместе с тем контражурное освещение очень эффектное и является весьма выразительным для выявления контрастности изображений.

Заметим, что на картине расстояние Солнца до линии горизон­та может быть разным. Если точка схода солнечных лучей от линии горизонта находится высоко, то положение Солнца соответствует полуденному времени дня. При восходе и закате Солнца точка схо­да солнечных лучей находится на небольшом расстоянии от горизон­та, поэтому падающие тени от предметов будут очень длинными и к краям расплывчатыми.

Солнце находится за зрителем. В этом случае солнечные лучи являются нисходящими параллельными прямыми общего (или осо­бого) положения. На основе законов перспективы известно, что нисходящие параллельные прямые имеют точку схода под линией горизонта, а их проекции — на горизонте.

Следовательно, если Солнце находится за зрителем и тени от предметов направлены перпендикулярно к основанию картины, то точка схода солнечных лучей будет на линии главного вертикала под горизонтом, а ее проекция — в главной точке. В этом случае солнеч­ные лучи будут нисходящими прямыми особого положения (илл. 253,а). Поэтому тени от цилиндра и призмы при удалении уменьша­ются и направлены от зрителя к горизонту в главную точку.

Если точка схода солнечных лучей смещена относительно ли­нии главного вертикала, то при таком положении Солнца падаю­щая тень от предметов направлена влево или вправо от зрителя.

В этом случае солнечные лучи будут нисходящими прямыми обще­го положения (илл. 253,6).

Когда Солнце находится за зрителем, то предмет обращен к нему своей освещенной стороной, а его затемненная часть видна незначительно. В этом случае объемная форма предмета выявляет­ся слабо и он воспринимается плоским. Такое освещение называ­ется фронтальным, или «лобовым», направленным «в лоб».

Солнце находится сбоку от зрителя. В этом случае солнечные лучи расположены параллельно картине и наклонены к предметной плоскости под произвольным (или заданным) углом, то есть они явля­ются фронтальными прямыми. По законам перспективы они не име­ют точки схода и остаются параллельными между собой, а их проек­ции параллельны основанию картины и являются прямыми широт.

Такое освещение называется «боковым», поэтому объемная форма предмета разделяется на светлую и темную половины или их части (илл. 254). Кроме того, падающие тени от вертикальных элементов призмы и цилиндра изображаются параллельными ос­нованию картины.

Рассмотрим примеры построения на картине падающих пре­ломленных теней от предметов при различном положении Солнца. Построим солнечную тень, падающую от вертикального предмета на ступени лестницы, если Солнце находится сзади зрителя и сле­ва от него (илл. 255). Сначала зададим справа от объекта (посколь-

ку Солнце слева) точку схода солнечных лучей (CJ под линией го­ризонта и ее проекцию (с») на горизонте. Затем проведем солнеч­ный луч через верхний конец (А) вертикального предмета в точку схода С_м а его проекцию — через нижний конец (В) в точку схода _Соо. Далее определим линию пересечения лучевой вертикальной плоскости со ступенями лестницы. Заметим, что направление уча­стков тени будет соответствовать вертикальному и горизонтально­му положению плоскостей ступеней. Тени на ступенях будут иметь точку схода с

Построим тень, падающую от парапета на ступени лестницы, если Солнце находится перед зрителем и слева от него (илл. 256). Сначала зададим точку схода солнечных лучей (CJ и ее проекцию (с»»). Затем построим тени от ребер парапета — левого вертикаль­ного и горизонтального (1—2), определяющего его толщину. Заме­тим, что тень 1. — 2. параллельна ребру 1—2, поэтому они имеют общую точку схода F_t.

Для построения конту-
ра тени на вертикальных
плоскостях ступеней от
наклонного ребра парапета
(2 — 5) отметим на нем точ-
ки 3 и 4. Через них прове-

дем солнечные лучи в вертикальных плоскостях ступеней. С этой
целью построим проекцию святящейся точки (Солнца) на данную
ПЛОСКОСТЬ (с'оо^ Fj).

Тогда лучи С'^ — 3 и С'^ — 4 определят контур теней, проходящих через точки 3 и 4 в вертикальных и горизонтальных плоскостях сту­пеней. Заметим, что ребра горизонтального участка парапета и тени от него направлены в точку схода F₂. Данный пример часто встреча­ется при построении солнечных теней от архитектурных объектов.

Построим солнечные тени, падающие от лестницы и доски, приставленных к стене, если Солнце находится сбоку от зрителя с левой его стороны (илл. 257).

Сначала зададим точки опоры лестницы на земле (3 и 4), а за­тем определим вторую пару (1 и 2) на стене. Для этого через концы лестницы (3 и 4) проведем параллельные прямые в точки схода F,

F₂■ Определив пересечение их с основанием стены, проведем вертикальные прямые и отметим опорные точки 1 и 2. Построим боковые жерди лестницы (1—3 и 2—4), на которых отложим три перекладины на равном расстоянии друг от друга.

Теперь построим падающую тень от лестницы. Заметим, что тени от опорных точек с ними совпадают. Чтобы определить пре­ломление тени, сначала построим ее на земле от точек 1 и 2. Соеди нив попарно точки 1, — 3„ и 2,-4., определим тень от наклонных жердей лестницы на горизонтальной плоскости. Далее; точки пере­сечения тени с основанием стены соединим с опорными (1,-2,).

Теперь построим тени от перекладин лестницы. Для этого че-
рез их концы на ближней жерди проведем световые лучи до пере-
сечения с ее тенью и через них проведем тени от перекладин в точку
схода F_x. Обратим внимание, что расстояние между тенями от пе-
рекладин на земле и на стене разное. Аналогично построены пада-
ющие тени от доски.

Построим солнечную тень от горизонтального навеса на стену
дома, если Солнце находится сбоку от зрителя (илл. 258). Сначала
на стене построим падающие тени от дальнего (1) и ближнего (2)
углов навеса. Для этого через точки 1 и 2 проведем солнечные лучи

в заданном на- правлении, а их
проекции — па-
раллельно основа-
нию картины. За-
метим, что контур
тени І. 2 * от ребра

1— 2 будет иметь
общую точку схо-
да F_t. Затем опре-
делим тень от вер-
тикального ребра

навеса, проходящего через точку 2, и горизонтальных ребер, перпендикулярных к плоскости стены. По этим же точкам построим тени от опорных стоек перил.

Тень в дверном проеме от навеса определим с использованием точки 3. Через полученную точку 3. проведем тень от его края в точку схода Fx. Тень от боковой и верхней стенок проема построим по точке 4. В оконном проеме падающую тень от его угла (5.) построим по точке 5. Тени от перил видны по построениям на рисунке.

Рассмотрим построение солнечной тени от цилиндрического навеса и вертикальной стенки, падающих на цилиндрическую колонну и горизонтальную плоскость при положении Солнца сзади

зрителя (илл. 259). т- ~ ■■■-

Сначала проведем в точку проекции солнечных лучей
касательно к осно-
ванию цилиндра и
определим на нем
собственную тень и
контур падающей
тени. От цилин-
дрического навеса
падающая тень по-
строена способом

описанного квадра­та. Эти построения известны, поэтому они не показаны.

Затем проведем проекцию светового луча через верхний конец собственной тени цилиндра и в плоскости навеса отметим точку 1. От нее построим тень Ц при пересечении солнечного луча с конту­ром собственной тени цилиндра. Произвольно задав на краю наве­са ряд точек (2, 3, 4), проведем через них световые лучи с их про­екциями и определим от них тени на колонне. Поясним, что для определения тени 4. проведем проекцию светового луча через верх­ний конец (4) контурной образующей цилиндра.

Таким же образом построим падающую тень от вертикальной плоскости доски на цилиндрическую поверхность, проведя световые лучи и их проекции через произвольно выбранные точки А, В и Е.

Солнечные падающие тени играют большую роль при выпол­нении этюдов на пленэре, рисовании с натуры интерьера или на­тюрморта в дневное время. В этом случае тени строят при фик­сированном одномоментном положении солнца. Особенности подвижности солнечного освещения следует учитывать при рисо­вании с натуры натюрморта в дневное время (илл. 260). Если сол­нечное освещение контражурное, то тени от всех предметов на­тюрморта будут иметь четкое очертание, поскольку направлены на зрителя и находятся близко к основанию картины. Падающие тени являются составной частью общей композиции, поэтому их

надо строить по пра-
вилам перспективы
для определения бо-
лее точного контура.

Если постановка
натюрморта находит-
ся в глубине помеще-
ния и далеко от окна,
то освещение будет
рассеянным и сол-
нечные тени от пред-
метов будут нечетки-
ми, расплывчатыми,

и тогда отпадает необходимость их точного построения.

При выполнении этюдов или рисунков с натуры на открытом воздухе очень важно при подвижности солнца учитывать освеще­ние объектов, а также направление падающих теней, чтобы они были составной частью композиции. Определив такой момент, его надо зафиксировать. Для этого в соответствии с положением и направле­нием солнечных лучей задается их точка схода, а на линии горизонта ее проекция. Только после этого можно строить падающие; тени от всех характерных точек объектов. В качестве примера дан пленэр­ный рисунок с изображением окраины села (илл. 261).

11. Окружность в перспективе. Общие положения. Способы построения окружности в перспективе. Построение окружности, расположенной в плоскостях перпендикулярных картине.

Существует несколько способов построения, наиболее простой из

них – построение отдельных точек этой окружности (восемь), вписанной в

квадрат.

Предварительно строится квадрат с осями и диагоналями, затем опре-

деляются восемь точек: четыре точки (1, 2, 3, 4) касания к сторонам квадрата

и четыре точки (5, 6, 7, 8) пересечения окружности с диагоналями квадрата

(рис. 14). В перспективе для нахождения четырех точек на диагоналях квад- рата можно использовать простое построение, применяемое в техническом

рисунке:

1) точки 1, 2, 3, 4 – пересечение осей со сторонами квадрата;

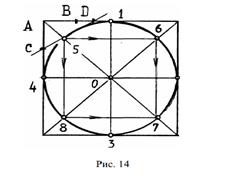
2) при вершине A квадрата с помощью дополнительных диагоналей

делят пополам половины смежных сторон, получают точки Ви С;

3) отрезокB-1 делят такимже образом пополам и получают точку D;

4) соединяют С и D, прямая CD в пересечении с диагональю квадрата

даст точку 5;

5) параллельным переносом находят положение остальных точек на

диагоналях квадрата (6, 7 и 8);

6) плавно соединяют восемь точек, на ортогональном изображении

(рис. 14) получается окружность, в аксонометрии и в перспективе – эллипс.

Построение перспективы окружности в горизонтальной плоскости по-

казано на рис. 15.

Построению перспективы окружности предшествует создание перспек-

тивы квадрата. Если две стороны квадрата параллельны основанию картины,

используют дистанционную точку D. Если дистанционная точка окажется за

пределами чертежа, можно воспользоваться дробной дистанционной точкой

D/2, проведя перспективу диагонали полуквадрата – прямую 4-D/2 (штрихо-

вая линия).

После построения перспективы квадрата определяют его центр пересе-

чением диагоналей и проводят оси, одна из которых на чертеже параллельна

горизонту, а другая имеет своей точкой схода точку P на линии горизонта.

Оси квадрата в пересечении со сторонами дали точки 1, 2, 3, 4.

Построение точек 5, 6, 7, 8 производят рассмотренным выше способом.

При вычерчивании кривой эллипса в перспективе необходимо иметь в

виду, что точка O – перспектива центра (точка пересечения диагоналей квад-

рата) и точка M – геометрический центр эллипса не совпадают.

Построение перспективы окружности в вертикальной плоскости анало-

гично, что видно из чертежа.

Примеры построения перспективы с использованием делительного

масштаба, вписыванием окружности и других операций даны на рис. 16, 17

и 18.

12. Общие сведения о теории теней. Понятие о собственных и падающих тенях. Виды и источники освещения. Алгоритм построения теней в перспективе.

Сначала определим некоторые понятия, связанные с освещен-
ностью предметов и передачей их объемной формы. Рассматривая
окружающие предметы, легко заметить, что степень их освещен-
ности различна. Наиболее светлыми бывают те поверхности, на
которые лучи света падают под прямым углом, и яркость их усили-
вается при более близком положении источника освещения к
объекту. С уменьшением угла наклона световых лучей к поверхно-
сти яркость ее освещенности ослабевает. Наиболее темной являет-
ся та часть предмета, на которую лучи света не попадают совсем —
это собственная тень. Если освещен какой-либо плоскогранный предмет (илл. 230,а),
то переход от светлой части к теневой осу-
ществляется четкой границей ребер. Если

предмет имеет круг-
лую форму (илл. 230,

б), то градация пере-
хода от освещенной
части к теневой осу-
ществляется более
мягко и плавно. Та-
ким образом, града-
ция светотени пред-
мета выявляет его

Известно, что освещение может быть искусственным и есте­ственным (природным). Искусственный источник света, как правило, расположен на близком расстоянии от предмета, и в тео­рии перспективы его называют светящейся точкой, или факе­лом. Примером искусственного источника света являются элект­рическая лампочка в комнате, прожектор, фонарь на улице, софит на сцене, пламя свечи и спички и пр. При точечном (факельном) освещении пучок лучей направлен из одной точки (илл. 231,а).

Дата добавления: 2015-05-29