Перспектива плоскостей частного положения

II. ПЕРСПЕКТИВА ПЛОСКОСТИ

Линии, проходящие через точку зрения S (центрально- проецирующие прямые).

Такие линии в перспективе проецируются в точку, а вторичные проекции – в вертикальные прямые (рисунок 20).

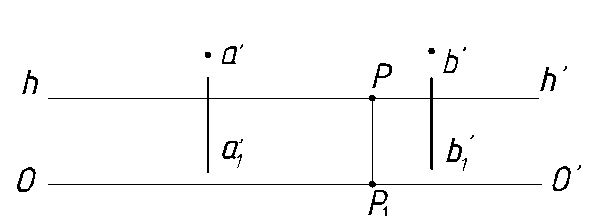
Рисунок 20

В перспективе, как и в ортогональных проекциях, плоскость может быть задана при помощи:

- трех точек, не лежащих на одной прямой;

- прямой и точки, не лежащей на этой прямой;

- двух пересекающихся или параллельных прямых;

- плоской фигуры;

- следов (рисунок 21)

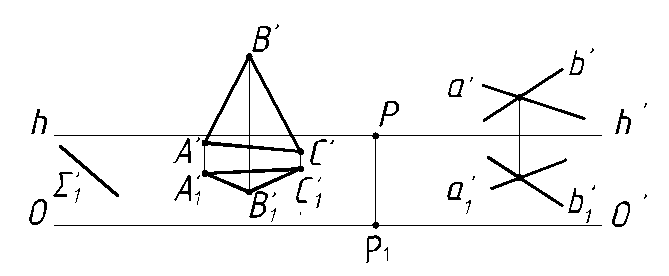
Рисунок 21

Перспектива плоскости строится как перспектива точек и прямых, определяющих эту плоскость.

На рисунках 22, 23 построена перспектива плоскости методом Дюрера.

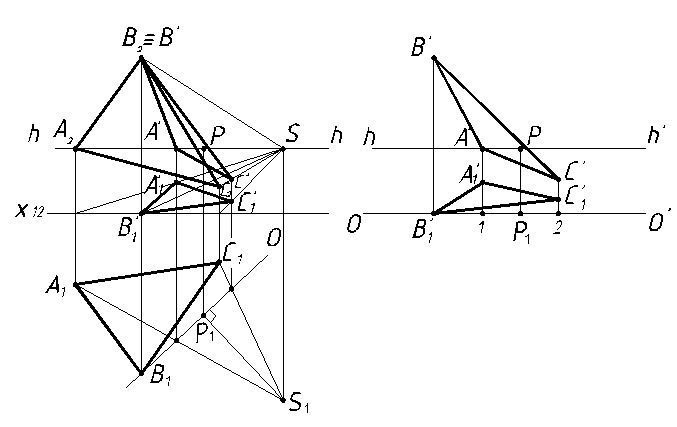Рисунок 22 Рисунок 23

а) Вертикальные плоскости. Они на предметную плоскость проецируются в прямые линии, следовательно, их вторичные проекции будут в виде прямых (рисунок 24).

Рисунок 24

Плоскость задана предметным следом. Если предметный след продолжить до пересечения с картинной плоскостью, то картинный след плоскости можно провести перпендикулярно основанию картинной плоскости (рисунок 25).

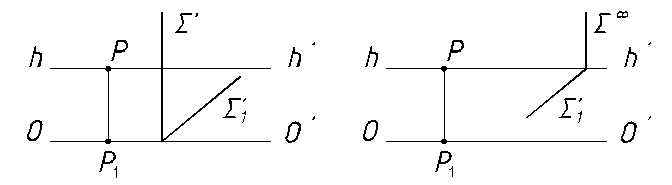
Рисунок 25 Рисунок 26

Если предметный след продолжить до пересечения с линией горизонта, то перпендикулярно линии горизонта можно провести перспективу бесконечно удаленной прямой плоскости или линию схода перспектив плоскостей, параллельных данной (рисунок 26).

б) Центрально- проецирующие плоскости (плоскости, проходящие через точку S). Перспективы таких плоскостей будут в виде прямых (рисунок 27).

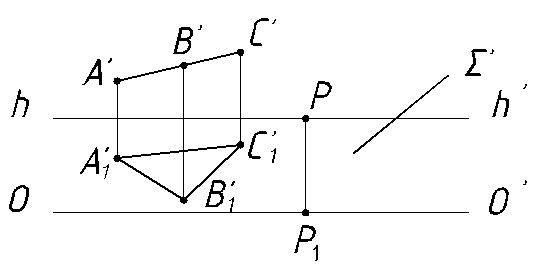
Рисунок 27

с) Центрально-проецирующие вертикальные плоскости (плоскости, перпендикулярные предметной плоскости и проходящие через точку S). Их перспективы и вторичные проекции в виде прямых линий (рисунок 28).

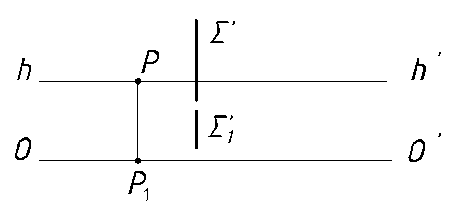
Рисунок 28

Рассмотрим еще один способ построения перспективы с ортогонального чертежа.

Дата добавления: 2015-05-29