Билет 18. Теплопередача через плоскую стенку, граничное условие 1рода

Билет 17. Начальные условия.

Дана однородная и изотропная стенка (рис.3) толщиной δ с постоянным коэффициентом теплопроводности λ, два других размера стенки неограниченны. На наружных поверхностях стенки поддерживают постоянные температуры t1 и t2. При заданных условиях температура будет изменяться только в направлении оси Ox, т.е. температурное поле будет одномерным и ∂t/∂y = ∂t/∂z = 0 Тогда уравнение (24) принимает вид: d2t/dx2=0 в уравнении (25) частная производная заменена полной, т.к. изменение температуры определяется только одной переменной X. Граничные условия в рассматриваемой задаче запишутся следующим образом: при х=0 t=t1 при b t=t2 В результате поставленной задачи должно быть найдено распределение температуры в плоской стенке, т.е. t = ƒ(x), и получена формула для определения плотности теплового потока. Проинтегрируем дважды уравнение (25). Первое интегрирование дает: dt/dx=c1 После второго интегрирования получим: t=c1x+c2 Постоянные интегрирования в (28) определяются из граничных условий (26): при х=0 t=t1 и c2=t1 при х=b t=t2 c1=t2-t1/b=t1-t2/b Подставляя значения С1 и С2 в уравнение (28), получим закон распределения температуры в рассматриваемой плоской стенке или, иначе, выражение для температурного поля: t=t1-(t1-t2/b)*x Для определения плотности теплового потока воспользуемся законом Фурье q=-λdt/dx Учитывая, что dt/dx=c1=-t1-t2/b после подстановки dt/dx в выражение закона Фурье, получаем: q=λ/b(t1-t2) В уравнении (30): t1 - t2 = Δt - температурный напор; отношение λ/δ, Вт/м2К- тепловая проводимость стенки; обратная величина Rc = δ/λ, м2К/ Вт - термическое сопротивление теплопроводности стенки. Найдя gлотность теплового потока, можно вычислить все тепло, которое передается через поверхность стенки F за время τ: Q=qFτ=λ/b(t1-t2)Fτ (31)

Билет 20. Теплопередача через плоскую стенку, граничное условие 3рода. 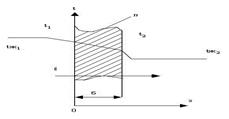Передача теплоты от одной среды (жидкости или газа) к другой через разделяющую их твердую стенку любой форма называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплопередачу от стенки к более холодной среде. Вначале рассмотрим теплопередачу через однослойную стенку. Пусть плоская безграничная однослойная стенка имеет толщину δ (рис.5). Задан коэффициент теплопроводности λ. Граничными условиями Ш рода заданы температуры сред tж1 и tж2, а такте коэффициенты теплоотдачи α1 и α2. Величины tж1, tж2, α2, α1 постоянны и не меняются вдоль поверхности, что дает основании считать, что температура меняется только в направлении оси Ох. При заданных условиях необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхности степени t1 и t2. При стационарном тепловом режиме плотность теплового потока, передаваемого теплоотдачей, от горячей среды к стенке, равна плотности теплового потока, передаваемого теплопроводностью, через стенку и равна плотности теплового потока, передаваемого теплоотдачей, от стенки к нагреваемой среде. Тогда, используя уравнения (20 и 30), запишем q=a1(tж1-t1) q=λ/b(t1-t2) q=a2(t2-tж2) Уравнения (35) запишем в виде: tж1-t1=q*1/a1 t1-t2=qb/λ t2-tж2=q*1/a2 (36)

Просуммировав (36), получим:tж1-tж2=q(1/a1+b/λ+1/a2) Отсюда плотность теплового потока, Вт/м2 q=tж1-tж2/1/a1+b/λ+1/a2 Обозначим: k=1/1/a1+b/λ+1/a2 вт/м2к К - коэффициент теплопередачи. Коэффициент теплопередачи К характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус. С учетом (38) уравнение (37) можно записать в виде q=K(tж1-tж2) Величина, обратная коэффициенту теплопередачи, называется термическим сопротивлением теплопередачи: R=1/K=1/a1+b/λ+1/a2 (40)

Билет21. Коэффициент теплопередачи.- Передача теплоты от одного теплоносителя к другому через твердую стенку называется теплопередачей. Количество передаваемой теплоты определяется основным уравнением теплопередачи: Q = K·F· t ср Q – тепловой поток, т.е. Количество теплоты, передаваемое через поверхность теплообмена в 1 с, Вт; K – коэффициент теплопередачи, Вт/м 2 ·К; t ср – средняя разность температур горячего и холодного теплоносителя,К; F – площадь поверхности теплопередачи,м 2 Коэффициент теплопередачи К показывает, какое количество теплоты переходит в единицу времени от более нагретого к менее нагретому теплоносителю через разделяющую их стенку площадью 1м 2 в течение 1с при средней разности температур между теплоносителями 1К. Плотность теплового потока: q = Q/F = K t ср

Билет22. Термическое сопротивление теплопередачи.- величина обратная теплового проводимости стенки b/λ м2град/Вт

Билет23. Теплопередача через цилиндрическую стенку, граничное условие 1рода Рассмотрим стационарный процесс теплопроводности в цилиндрической стенке (трубе) с внутренним диаметром d₁= 2 r₁ и наружным диаметром d₂= 2 r₂ (рис).
На поверхностях стенки заданы постоянные температуры t_c1 и t_c2. В заданном интервале температур коэффициент теплопроводности материала стенки λ является постоянной величиной. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее.

Рис.Теплопроводность цилиндрической стенки.

В рассматриваемом случае дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе координат:

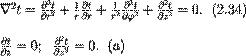
Когда коэффициент теплопроводности является функцией температуры вида λ (t)= λ₀ (1+ bt), можно показать, что линейную плотность теплового потока можно вычислить по той же формуле, что и для λ =const:

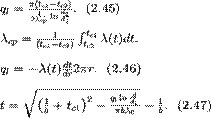
λ_cp – среднеинтегральное значение коэффициента теплопроводности. Для нахождения температурного поля при λ = λ (t)= λ₀ (1+ bt) можно воспользоваться уравнением закона Фурье, записанного для цилиндрической стенки - выражение (2.46). Если разделить переменные и проинтегрировать уравнение (2.46) в пределах от r=r₁ до r и от t=t_c1 до t и найти из полученного интеграла t, то получим выражение для температурного поля - выражение (2.47

Дата добавления: 2015-05-26