Билет24. Теплопередача через цилиндрическую стенку, граничное условие 2рода

Билет25. Теплопередача через цилиндрическую стенку, граничное условие 3рода. Рассмотрим однородную цилиндрическую стенку (трубу) с постоянным коэффициентом теплопроводности λ. Заданы постоянные температуры подвижных сред t _F1 и t _F2 и постоянные значения коэффициентов теплоотдачи на внутренней и наружной поверхностях трубы 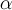₁ и 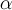₂ (рис. 2.7).

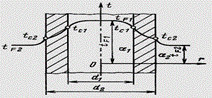
Рис. 2.7. Теплопередача через однородную цилиндрическую стенку. Согласно теории теплопередачи, зависимость теплового потока через изолированную стенку трубы от толщины изоляции следующая: сначала тепловой поток растет за счет увеличения диаметра поверхности, достигает максимума при критической толщине изоляции, и далее снижается. Критический диаметр изоляции = 2 * коэффициент теплопроводности изоляции / коэффициент теплоотдачи от наружной поверхности изоляции воздуху.

Билет29. Вынужденная и естественная конвекция. При вынужденной конвекции движение жидкости обусловлено внешними по отношению к рассматриваемому процессу тепло- или массообмена причинами (например, действием какого-либо побудителя: насоса, компрессора, вентилятора и т.п.)При свободной конвекции движение жидкости обусловлено самим процессом тепло- или массообмена, а именно, силами, возникающими вследствие неоднородности поля плотности, что в свою очередь связано с неоднородностью поля температур (при теплообмене) или концентраций (при массообмене) Билет31. Пограничный слой. Пограничный слой- это временная в потоке тонкая зона, вблизи тв. поверхности, в которой поперечный градиент скорости настолько велик,что пренебрегать влиянием внутреннего трения нельзя, их необходимо учитывать.По мере удаления от передней кромки пластины, толщина пограничного слоя возрастает, поскольку возмущенное влияние стенки проникает все дальше, в невозмущенный поток вследствие поперечного переноса импульса.Тепл. погран. слой хар-ся тем,что в пределах его толщ. имеет место градиент температуры=> перенос тепла поперек потока молеклуярной теплопроводности(при ламинарном режиме).Вектор плотности потока массы ρw(vector) Ламинарное движение – это упорядоченное (слоистое) движение жидкости. При ламинарном режиме частицы жидкости движутся по плавным, непересекающимся траекториям, а все хар-ки потока представляют собой плавно изменяющиеся, гладкие функции координат и времени. При турбулентном режиме частицы жидкости движутся по сложным, ломанным, многократно пересекающимися траекториями, а все характеристики потока представляют собой пульсирующие, скачкообразно и хаотически изменяющиеся функции координат и времени. Режим движения зависит от соотношения сил внутреннего трения и инерции Билет32. Дифференциальные уравнения конвективного теплообмена. уравнение, описывающее процесс теплоотдачи на границах тела. Так как у поверхности твердого тела имеется слой неподвижной жидкости, то для этого слоя можно использовать закон Фурье. Принимая, что ось Оу направлена перпендикулярно поверхности, запишем Однако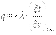

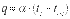
Приравнивая эти уравнения получим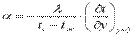

.

Уравнение называют дифференциальным уравнением теплоотдачи.

Если в дифференциальное уравнение теплопроводности подставить конвективное изменение температуры, обусловленное течением жидкости:

.

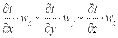где w_x, w_y и w_z – проекции скорости жидкости на координатные оси, то можно записать

.

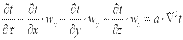Иными словами говоря, если через изучаемый нами элементарный объём движется со скоростью w некое температурное поле, то дифференциальное уравнение теплопроводности следует накладывать на это поле.

Для строго описания процессов конвективного теплообмена к дифференциальному уравнению (10.3) следует добавить уравнение (Навье-Стокса) движения вязкой жидкости, вытекающее из второго закона Ньютона, уравнение сплошности и неразрывности жидкости и учесть зависимость плотности жидкости от температуры. Такая система уравнений описывает большой класс явлений — процессы конвективного теплообмена между жидкостью и твердой стенкой. Эти уравнения должны быть дополнены условиями однозначности, характеризующими конкретные особенности той или иной рассматриваемой задачи.

Дата добавления: 2015-05-26