Работа сил электростатического поля. Потенциал

На заряд q' находящийся в электростатическом поле с напряжённостью Е действует сила F=q’*Е. При перемещении заряда q' эта сила будет совершать работу. Найдём выражение для работы вначале для частного случая. Пусть поле создаётся точечным зарядом q и в этом поле перемещается точечный заряд q'. Вычислим работу, которую совершают силы поля по перемещению этого заряда q'.

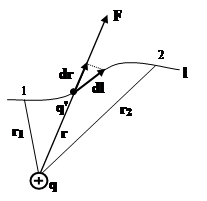
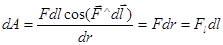Пусть заряд q' переместился из положения 1 в положение 2 по некоторой траектории. Рассмотрим бесконечно малый отрезок этой траектории dl. Работа на этом отрезке будет равна:

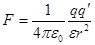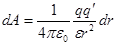На всём пути работа будет равна:

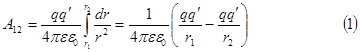Из полученной формулы видно, что работа по перемещению заряда q' определяется только начальным и конечным положением заряда q' (т.е. r₁ и r₂) и, следовательно, не зависит от пути по которому перемещается заряд. В механике мы видели, что поле, работа в котором не зависит от пути перемещения, называется потенциальным, а силы этого поля называются потенциальными или консервативными. Таким образом, электростатическое поле создаваемое точечным зарядом является потенциальным. Можно показать, что и поле создаваемое любой системой неподвижных зарядов является потенциальным.

Из механики известно, что работа на замкнутом пути в потенциальном поле равна нулю. Для электростатического поля это можно записать так:

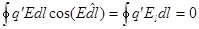где Е_l-проекция вектора E на элемент перемещения dl

-это есть математическое выражение потенциального характера электростатического поля.

Выражение

называется - циркуляцией вектора напряжённости.

Из (2) следует, что циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю. Это справедливо только для электростатического поля. Для поля движущихся зарядов это не выполняется.

Из механики известно, что тело, находящееся в потенциальном поле, обладает потенциальной энергией, а работа, совершаемая полем при перемещении тела равна убыли потенциальной энергии. Поскольку электростатическое поле также является потенциальным, работу по перемещению заряда q'(1) можно представить как разность значений потенциальной энергии, которыми обладает заряд q' в точках 1 и 2 поля заряда q.

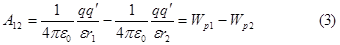Отсюда для потенциальной энергии заряда q' в поле заряда q получаем:

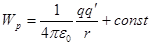В выражении для потенциальной энергии значение постоянной обычно выбирается таким образом, чтобы при удалении заряда на бесконечность потенциальная энергия обращалась в ноль.

отсюда const=0, и при этом условии имеем:

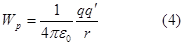Следует отметить, что строго говоря, потенциальная энергия (4) как и в механике, должна рассматриваться как потенциальная энергия взаимодействия точечных зарядов q и q' находящихся на расстоянии r друг от друга. Но поскольку мы рассматриваем, что поле создаётся зарядом q и в этом поле движется заряд q', то выражение (4) можно называть потенциальной энергией заряда q' в электрическом поле, созданном зарядом q.

Из выражения (4) видно, что потенциальная энергия зависит как от величин, характеризующих поле (q и r), так и от величины заряда q' вносимого в это поле. Если помещать в одну и ту же точку поля (r=const) различные заряды q',q'' и т.д., то они будут обладать различной потенциальной энергией W'_P, W''_p.

Однако отношение:

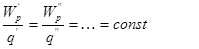для данной точки поля.

Следовательно, отношение W^’/q^’ является характеристикой только поля и не зависит от заряда q^’ вносимого в поле.

Величина

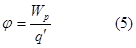называется потенциалом поля в данной точке и наряду с напряженностью поля Е является важной характеристикой электрического поля.

Из (5) следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля положительный единичный заряд.

Для потенциала поля точечного заряда из (5) и (4) получаем:

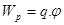Из (5) следует, что заряд q, находящийся в точке поля с потенциалом обладает потенциальной энергией:

Работа сил поля над зарядом q равна:

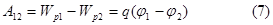Таким образом, работа, совершаемая при перемещении заряда силами поля, равна произведению заряда на разность потенциалов в начальной и конечной точках.

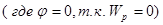Если заряд q из точки с потенциалом φ удаляется на бесконечность

работа сил будет равна

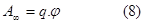Отсюда следует, что потенциал численно равен работе, которую совершают силы поля над положительным единичным зарядом при удалении его из данной точки на бесконечность.

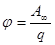Из соотношения (8) можно установить единицы измерения потенциала. За единицу потенциала следует принять потенциал в такой точке поля, при перемещении из которой в бесконечность поле совершает работу равную единице

В СИ единица потенциала называется вольтом:

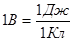Часто используется единица работы и энергии называемая электронвольтом (эв).

1 электронвольт есть работа, совершаемая силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов в 1в.

1эв=е*1в=1,6*10^-19Кл*1в=1,6*10^-19дж.

Пусть поле создаётся системой точечных зарядов q₁,q₂… Расстояние от каждого из зарядов до данной точки поля обозначим r₁,r₂… Поскольку потенциал является скалярной величиной, то очевидно, что потенциал поля создаваемой системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности:

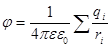В то время как напряжённости поля складываются при наложении полей векторно, потенциалы складываются алгебраически. Поэтому вычисление потенциалов обычно оказывается гораздо проще, чем вычисление напряжённостей электрического поля.

Дата добавления: 2015-05-31