Дисперсионный анализ в матричных обозначениях

Резюме

Для вычисления вектора 1 МНК оценок 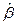для 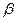достаточно применить формулу (5).

При этом порядок расчетов может быть следующим:

1) вычисляют произведение матриц ;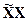

2) умножают матрицу регрессоров 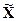на вектор регрессандов, то есть определяют вектор ;

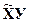3) находят матрицу, обратную матрице ;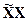

4) рассчитывают, какой является результатом произведения этой обратной матрицы и вектора .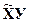

При традиционной компьютерной реализации регрессионного анализа необходимо ввести в компьютер только матрицу данных

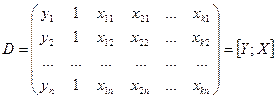(6)

и за несколько секунд будут рассчитанный оцененный вектор регрессионных коэффициентов и другие величины.

14.2. Интерпретация 1 МНК – оценок

Подставляя элементы вектора 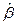(5) в оцениваемое уравнение, получим эмпирическую регрессионную функцию

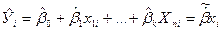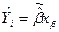или (7)

Эта функция определяет регрессионную гиперплоскость.

Эмпирический регрессионный коэффициент 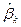в (7) есть частной производной эмпирической регрессионной функции по к-му регрессору.

Изменение величины к-го регрессора на единицу при прочих равных условиях вызовет изменение оцененной величины 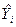на количество единиц, ровное значению .

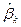14.3. 1 МНК – оценщик 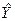величины. Математического ожидания вектора регрессанда.

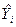- величина Y, лежащая на регрессионной гиперплоскости. Она есть точечным 1МНК – оценщиком величины математического ожидания регрессанда в период и и ровная 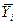- систематической (свободной от влияния возмущений) части регрессанда в этот период.

Величина - прогноз величины Y (точнее говоря, величины ее математического ожидания) что рассчитывается по эмпирическому регрессионному уравнению для периода I временных рядов или же для элемента и пространственных данных.

Все n значений 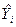(i=1.n) образуют вектор

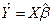(8)

14.4. 1МНК – оценщик 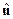вектора возмущений

Оцененный с помощью метода 1 МНК вектор возмущений запишется таким образом

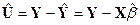(9)

Его также называют вектором ошибок.

Свойство вектора ошибок, полученного при оценивании методом 1 МНК, заключается в том, что сумма ошибок равна нулю

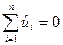(10)

Это свойство позволяет простым способом проверить, были ли сделаны ошибки в расчетах при вычислени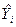и и .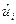

Вектор ошибок 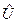иногда используют для расчета относительной ошибки прогноза. Для і-го наблюдения относительная ошибка прогноза равна (11)

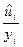или в процентах 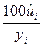(11)

14.5. 1МНК – оценщик дисперсии возмущений

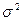- дисперсия возмущений 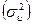является важной характеристикой регрессионной модели.

Ее величина должна быть как можно меньше 1 МНК – оценщик для 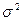определяется таким образом

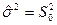= сумма квадратов ошибок - число степеней свободы =

или 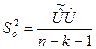(12)

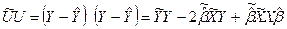
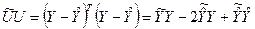
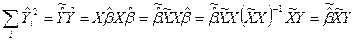
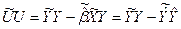
Тогда

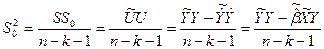(13)

Сумма квадратов ошибок вычисляется как разница между суммой квадратов n наблюдений регрессандов (кратко: суммой общих квадратов): 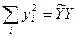, и суммой квадратов n регрессандов, рассчитанных по регрессии (кратко: суммой квадратов регрессии).

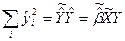
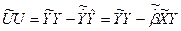(14)

SFQ=SGQ-SRQ (15)

Дата добавления: 2015-05-26