
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теплопередача
|
|
|
|
Это учение о процессах распространения теплоты. Теплота распространяется тремя принципиально различными способами: теплопроводностью, конвекцией и тепловым излучением.
Теплопроводность представляет собой процесс распространения тепловой энергии при непосредственном соприкосновении отдельных тел или частиц одного тела, имеющих различные температуры и обусловлена движением микрочастиц тела
Конвекция возможна только в текучей среде–жидкой или газообразной. Под конвекцией теплоты понимают процесс переноса тепловой энергии при перемещении объемов жидкости или газа в пространстве из области с более высокой температурой в область с пониженным ее значением. Перенос теплоты неразрывно связан с переносом самой среды.
Тепловое излучение – это процесс распространения тепловой энергии с помощью электромагнитных волн. Сопровождается двойным превращением энергии: тепловая энергия излучающего тела переходит в лучистую и обратно – лучистая энергия, поглощаясь телом, переходит в тепловую.
Условия и закономерности протекания элементарных явлений различны. В большинстве случаев один вид теплообмена сопровождается другим. Теплопроводность в чистом виде большей частью имеет место лишь в твердых однородных телах. Конвекция теплоты всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно соприкосновение отдельных частиц, имеющих различную температуру. Совместный процесс конвекции и теплопроводности называют конвективным теплообменом.
При инженерных расчетах определяют конвективный теплообмен между потоком жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей. Конвективная теплоотдача часто сопровождается теплоотдачей излучением.
В целом перенос теплоты от горячих газов к холодному воздуху через разделяющую их стенку представляет собой сложный процесс, который называют теплообменом или теплопередачей. В рабочем пространстве нагревательного устройства передача теплоты от нагретых газов к внутренней поверхности стенки будет происходить в основном путем излучения и конвекции, через саму стенку – путем теплопроводности и от наружной поверхности стенки в окружающее пространство – путем конвекции и излучения.
Следовательно, на отдельных этапах прохождения теплоты элементарные виды теплообмена могут находиться в самом различном сочетании.
Процессы теплообмена могут происходить в различных средах: в чистых веществах и разных смесях, при изменении и без изменения фазового состава. Часто процессы переноса тепловой энергии сопровождаются переносом вещества (процессы окисления, восстановления, разложения). При наличии массообмена процессы теплообмена значительно усложняются и будут описываться более сложными дифференциальными уравнениями.
1.1.Теплопроводность
Механизм теплообмена теплопроводностью обусловлен движением микрочастиц вещества. В газах перенос энергии осуществляется путем диффузии молекул и атомов, в жидкостях и твердых телах (диалектриках) – за счет упругих волн, в металлах – путем диффузии свободных электронов и упругих колебаний кристаллической решетки.
Процесс теплопроводности неразрывно связан с распределением температуры внутри тела. Поэтому при изучении процесса прежде всего необходимо установить понятия температурного поля и градиента температуры.
1.1.1.Температурное поле
Температура характеризует тепловое состояние тела и определяет степень его нагретости. Теплопроводность может иметь место только при условии, что в различных точках тела (или системы тел) температура неодинакова. В общем случае процесс передачи теплоты теплопроводностью в твердом теле сопровождается изменением температуры как в пространстве, так и во времени. Основной задачей теории теплопроводности и является изучение пространственно – временного изменения температуры, т.е. нахождение зависимости
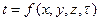 , (1.1)
, (1.1)
где  –координаты точек тела;
–координаты точек тела; 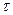 – временная координата.
– временная координата.
Уравнение (1.1) представляет собой математическое выражение температурного поля. Таким образом, температурным полем называется совокупность значений температуры во всех точках изучаемого пространства и для каждого момента времени.
Различают стационарное и нестационарное температурное поле. Уравнение (1.1) является записью наиболее общего вида температурного поля, когда температура изменяется с течением времени и от одной точки к другой. Такое поле отвечает неустановившемуся тепловому режиму теплопроводности и носит название нестационарного температурного поля.
Если тепловой режим является установившимся, то температура в каждой точке тела с течением времени остается неизменной, и такое температурное поле называют стационарным. В этом случае температура является функцией только координат
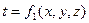 ;
;  . (1.2)
. (1.2)
Температурное поле, соответствующее уравнениям (1.1) и (1.2) является пространственным, так как температура – это функция трех координат. Если температура есть функция двух координат, то поле называют двухмерным:
 ;
;  . (1.3)
. (1.3)
Если температура является функцией одной координаты, то поле называют однородным:
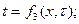

 . (1.4)
. (1.4)
Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:
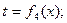
 и
и 
 . (1.5)
. (1.5)
Одномерной, например, является задача о переносе теплоты в стенке, у которой длину и ширину можно считать бесконечно большими по сравнению с толщиной.
1.1.2.Температурный градиент
При любом температурном поле в теле всегда имеются точки с одинаковой температурой. Если эти точки мысленно соединить, то можно получить изотермические поверхности, которые либо оканчиваются на поверхности тела, либо целиком располагаются внутри самого тела. Следовательно, температура в теле изменяется в направлении, пересекающем изотермы. При этом наибольший перепад температуры на единицу длины происходит в направлении нормали к изотермической поверхности (рис.1.1).
Предел отношения изменения температуры 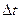 между соседними изотермами к расстоянию между ними по нормали
между соседними изотермами к расстоянию между ними по нормали  называется температурным градиентом и обозначается одним из следующих символов:
называется температурным градиентом и обозначается одним из следующих символов:

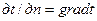
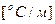 . (1.6)
. (1.6)
Это есть вектор, направленый по нормали к изотермической поверхности.
Положительным направлением температурного градиента считается направление в сторону возрастания температуры. Его значение, взятое с обратным знаком, называется падением температуры.
1.1.3.Тепловой поток. Закон Фурье
Теплота самопроизвольно переносится только в сторону убывания температуры. Количество теплоты, переносимой через какую–либо поверхность в единицу времени, называется тепловым потоком  . Тепловой поток, отнесенный к единице поверхности, называется плотностью теплового потока, или же удельным тепловым потоком, или же тепловой нагрузкой поверхности нагрева, т.е.
. Тепловой поток, отнесенный к единице поверхности, называется плотностью теплового потока, или же удельным тепловым потоком, или же тепловой нагрузкой поверхности нагрева, т.е.
 (1.7)
(1.7)
Если тепловой поток отнесен к единице изотермической поверхности, то величина 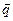 является вектором, направление которого совпадает с направлением распространения теплоты в данной точке и противоположно направлению вектора температурного градиента (рис. 1.2).
является вектором, направление которого совпадает с направлением распространения теплоты в данной точке и противоположно направлению вектора температурного градиента (рис. 1.2).
Изучая процесс теплопроводности в твердых телах, Фурье экспериментально установил, что количество переданной теплоты пропорционально температурному градиенту и площади сечения, перпендикулярного направлению распространения теплоты.
 . (1.8)
. (1.8)
Если количество переданной теплоты отнести к единице сечения и единице времени, то установленную зависимость можно записать в виде
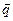
 (1.9)
(1.9)
Уравнение (1.9) является математическим выражением основного закона теплопроводности – закона Фурье, который лежит в основе всех теоретических и экспериментальных исследований процессов теплопроводности.
1.1.4.Коэффициент теплопроводности
Коэффициент пропорциональности  в уравнениях (1.8) и (1.9) является физическим параметром вещества, характеризующим способность тел проводить теплоту и называемым коэффициентом теплопроводности. Размерность – Вт/(м оС).
в уравнениях (1.8) и (1.9) является физическим параметром вещества, характеризующим способность тел проводить теплоту и называемым коэффициентом теплопроводности. Размерность – Вт/(м оС).
Определяет собой количество теплоты, которое проходит в единицу времени через один квадратный метр изотермической поверхности при температурном градиенте равном единице.
На величину коэффициента  влияет много факторов: температура, давление, структура, влажность, агрегатное состояние тела, механизм переноса теплоты и т.д.
влияет много факторов: температура, давление, структура, влажность, агрегатное состояние тела, механизм переноса теплоты и т.д.
Обычно определяют экспериментальным путем. Большинство методов основано на измерении теплового потока и градиента температур в заданном веществе.

Лучше определять из выражения:
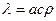 ,
,
где  – коэффициент температуропроводности, м2/с; с – теплоемкость, Дж/ (кг оС);
– коэффициент температуропроводности, м2/с; с – теплоемкость, Дж/ (кг оС); 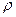 – плотность, кг/м3.
– плотность, кг/м3.
Так как температура в теле распределена неравномерно, то в первую очередь важно знать зависимость  от температуры. Для большого числа материалов эта зависимость оказывается почти линейной, т.е.
от температуры. Для большого числа материалов эта зависимость оказывается почти линейной, т.е.

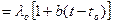 ,
,
где 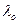 коэффициент теплопроводности при температуре
коэффициент теплопроводности при температуре 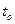 , Вт/(м оС);
, Вт/(м оС); 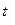 – температура, оС;
– температура, оС;  – температурный коэффициент, определяемый опытным путем.
– температурный коэффициент, определяемый опытным путем.
Лучшими проводниками теплоты являются металлы, у которых  изменяется от 3 до 458 Вт/(м оС). Самым теплопроводным металлом является чистое серебро (
изменяется от 3 до 458 Вт/(м оС). Самым теплопроводным металлом является чистое серебро ( =458 Вт/(м оС)).
=458 Вт/(м оС)).
Коэффициенты теплопроводности теплоизоляционных и строительных материалов, имеющих пористую структуру, при повышении температуры возрастают по линейному закону и изменяются в пределах от 0,02 до 3,0 Вт/(м оС). Для газов  изменяется в пределах от 0,006 до 0,6 Вт/(м оС).
изменяется в пределах от 0,006 до 0,6 Вт/(м оС).
Для капельных жидкостей  изменяется в пределах от 0,07 до 0,7 Вт/(м оС).
изменяется в пределах от 0,07 до 0,7 Вт/(м оС).
1.1.5.Общее дифференциальное уравнение теплопроводности
Для определения количества переданной теплоты необходимо знать коэффициент  и значение температурного градиента, а следовательно, и распределение температуру. Последнее относительно просто можно определить только для тел простой конфигурации – пластины, цилиндра, шара, куба и параллелепипеда. В общем же случае это распределение можно получить лишь в результате решения специального дифференциального уравнения теплопроводности.
и значение температурного градиента, а следовательно, и распределение температуру. Последнее относительно просто можно определить только для тел простой конфигурации – пластины, цилиндра, шара, куба и параллелепипеда. В общем же случае это распределение можно получить лишь в результате решения специального дифференциального уравнения теплопроводности.
Это уравнение выводится на основании закона сохранения энергии, сочетаемого с законом Фурье,
Согласно закону сохранения энергии количество теплоты 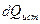 , выделенное внутренними источниками, за вычетом количества теплоты
, выделенное внутренними источниками, за вычетом количества теплоты 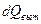 , вытекшего сквозь поверхность наружу, идет на приращение внутренней энергии вещества в выделенном объеме:
, вытекшего сквозь поверхность наружу, идет на приращение внутренней энергии вещества в выделенном объеме:
 =
= 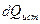 –
– 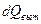 . (1.10)
. (1.10)
Выделим в теле элементарный параллелепипед со сторонами  (рис. 1.3)
(рис. 1.3)
Если объемную мощность тепловыделения, т.е. количество теплоты, выделяющейся в единице объема вещества за единицу времени обозначить через  , Вт/м3, то за время
, Вт/м3, то за время  получим:
получим:
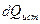 =
= 

 . (1.11)
. (1.11)
Для вычисления 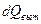 рассмотрим направление, определяемое осью х.
рассмотрим направление, определяемое осью х.
В этом направлении через левую грань поступает внутрь выделенного объема количество теплоты
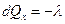


 .
.
Через противоположную грань за тот же промежуток времени вытекает из объема количество теплоты
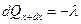






 .
.
Результативное количество вытекающей теплоты

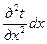

 .
.
Полное количество вытекающей из параллелепипеда теплоты во всех трех направлениях составит
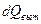

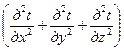
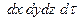 . (1.12)
. (1.12)
Приращение внутренней энергии вычисляется через теплоемкость и изменение температуры:
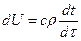
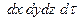 . (1.13)
. (1.13)
Здесь с в Дж/(кг оС), а 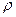 в кг/м3.
в кг/м3.
Подставив выражения (1.11), (1.12) и (1.13) в (1.10), получим
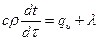
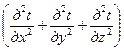 . (1.14)
. (1.14)
Введем в рассмотрение новую физическую характеристику вещества – коэффициент температуропроводности а, м2/с, определяемый из выражения
а 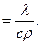
Он существенен для нестационарных тепловых процессов и характеризует скорость изменения температуры и является мерой теплоинерционных свойств тела. Скорость изменения температуры в любой точке тела будет, тем больше, чем больше коэффициент температуропрводности. При прочих равных условиях выравнивание температур происходит быстрее в том теле, которое обладает большим коэффициентом температуропроводности.
Уравнению (1.14) можно придать вид
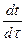
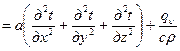 .
.
Физический смысл уравнения Фурье заключается в том, что им связывается пространственное распределение температуры с изменением ее во времени. Зная вблизи той или иной точки тела зависимость температуры от координат, можно предсказать, как быстро будет возрастать (или спадать) температура в этой точке при переходе к следующему моменту времени. Наиболее простое соотношение получается тогда, когда  =0, т.е. когда внутреннее тепловыделение отсутствует. При этом, чем больше коэффициент а, тем пропорционально быстрее меняется во времени температура.
=0, т.е. когда внутреннее тепловыделение отсутствует. При этом, чем больше коэффициент а, тем пропорционально быстрее меняется во времени температура.
Применительно к пространственным задачам стационарной теплопроводности  /
/ 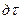 =0 и при
=0 и при  =0 уравнение Фурье приобретает вид
=0 уравнение Фурье приобретает вид
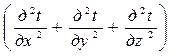 = 0;
= 0;  .
.
В цилиндрических координатах уравнение (1.15) записывается в виде:
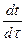
 , (1.16)
, (1.16)
где  – радиус вектор;
– радиус вектор; 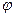 – полярный угол,
– полярный угол, 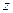 – аппликата.
– аппликата.
1.1.6.Условия однозначности решения
Полученное дифференциальное уравнение Фурье описывает явление передачи теплоты теплопроводностью в самом общем виде. Для того, чтобы применить его к конкретному случаю, необходимо знать распределение температур в теле в начальный момент времени (начальные условия). Кроме того, должны быть известны геометрическая форма и размеры тела, физические параметры среды и тела, граничные условия, характеризующие распределение температуры на поверхности тела, или взаимодействие изучаемого тела с окружающей средой.
Все эти частные особенности совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности и называются условиями однозначности или краевыми условиями,
Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальное условие аналитически может быть записано в виде
При 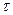 =0
=0 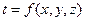 .
.
При 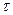 =0
=0 
Граничные условия, характеризуют взаимодействие рассматриваемого тела с окружающей средой. Задаются несколькими способами.
Граничные условия первого рода. Задается распределение температуры на поверхности тела для каждого момента времени


К ним относятся задачи разогрева и охлаждения системы при заданном изменении температуры на границе и т.д.
Граничные условия второго рода. Задаются величины теплового потока для каждой точки поверхности тела и любого момента времени
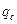 =
= 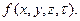
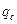 =
= 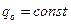 .
.
К ним относятся задачи нагрева системы внешним источником – нагревателем.
Граничные условия третьего рода. Задается температура окружающей среды  и закон теплообмена между поверхностью тела и окружающей средой. Для описания процесса теплообмена между поверхностью тела и средой используется закон Ньютона-Рихмана. Согласно этому закону количество теплоты, отводимое единицей поверхности тела в единицу времени, пропорционально разности температур между поверхностью тела
и закон теплообмена между поверхностью тела и окружающей средой. Для описания процесса теплообмена между поверхностью тела и средой используется закон Ньютона-Рихмана. Согласно этому закону количество теплоты, отводимое единицей поверхности тела в единицу времени, пропорционально разности температур между поверхностью тела  C и окружающей средой
C и окружающей средой  (
( >
>  ).
).
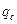 =
=  (
( –
–  ), (1.17)
), (1.17)
где  – коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2 оС).
– коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2 оС).
Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен количеству теплоты, отдаваемой (или воспринимаемой) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в 1 оС.
Согласно закону сохранения энергии количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие теплоотдачи (1.17), должно равняться количеству теплоты, подводимой к единице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела (1.9)¸т.е.
 ,
,
где n – нормаль к поверхности тела; с – индекс указывает на то, что температура и температурный градиент относятся к поверхности тела при n=0.
Окончательно граничные условия третьего рода можно записать в виде
 –
– 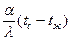 . (1.18)
. (1.18)
Граничные условия четвертого рода. Их задание определяется условиями теплообмена системы тел или тела с окружающей средой по закону теплопроводности. Предполагается, что между телами осуществляется идеальный контакт и температуры соприкасающихся поверхностей одинаковы.
При этом имеет место равенство тепловых потоков, проходящих через поверхность соприкосновения, т.е.
 . (1.19)
. (1.19)
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 1008; Нарушение авторских прав?; Мы поможем в написании вашей работы!