Анализ моделей краткосрочного страхования жизни

Страховая компания заключила N договоров страхования сроком на 1 год. Компания выплачивает наследникам: 100000 руб., если застрахованный умрет от несчастного случая, и 25000 руб., если застрахованный умрет от естественных причин в течение года. Компания не платит ничего, если застрахованный проживет этот год. Застрахованные разбиты на две возрастные группы численностью N₁ и N₂ человек (N=N₁+N₂). Вероятность смерти от естественных причин и от несчастного случая 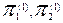для застрахованных 1-ой группы, имеющих возраст S₁ лет, и соответствующие вероятности для застрахованных 2-ой группы, имеющих возраст S₂ лет, рассчитываются с помощью модели Мейкхама или с помощью таблицы продолжительности жизни. Найти нетто-премию, страховую надбавку, цену полиса для застрахованных 1-ой и 2-ой групп в предположении, что вероятность неразорения компании будет не менее 0,95. Привести решения, использующие пуассоновское и гауссовское приближения.

Исходные данные для различных вариантов приведены в таблице1 (см. приложение 9).

Рассмотрим следующий вид страхования жизни. Человек платит страховой компании р руб. (эта сумма называется страховой премией — premium), а компания соглашается выплатить наследникам застрахованного а руб. в случае его смерти от естественных причин, руб. в случае смерти застрахованного от несчастного случая в течение года (и не платит ничего, если этот человек не умрет в течение года). Величины страховых выплат (benefit), конечно, много больше, чем страховая премия: a ≥ p, b ≥ p и поиск «правильного» соотношения между ними — одна из важнейших задач актуарной математики.

Отметим, что индивидуальный иск застрахованного 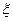является случайной величиной. В рассматриваемой нами схеме страхования распределение случайной величины имеет вид:

,

где , — вероятности смерти застрахованного в течение года от естественных причин и от несчастного случая соответственно ().

Средняя величина иска есть

,

дисперсия

,

а среднее квадратичное отклонение обозначим .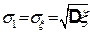

Часто удобнее представлять случайную величину 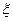в виде произведения двух величин:

;

где — индикатор события, состоящего в наступлении страхового случая:

,

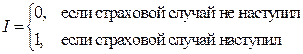а — величина иска при условии, что был страховой случай.

В рассматриваемой нами схеме страхования случайная величина 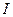имеет распределение

, ,

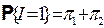также является случайной величиной, причем .

Наряду с величиной , описывающий индивидуальный иск, введем новую случайную величину , которая описывает «доход» компании от заключенного договора страхования. Она имеет ряд распределения:

,

Средний доход компании равен . Ясно, что средний доход компании должен быть неотрицательным, т. е. и минимально возможное значение равно 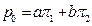. Оно соответствует нулевой средней прибыли компании и называется нетто-премией (net premium).

Совместное распределение величин 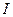и имеет вид:

b I ициентов тренда приведены в [	0	а	b
	p0
1		p1	p2

Условное распределение иска при условии, что он действительно предъявлен, есть

,

,

.

Найдем условное математическое ожидание иска при условии, что он предъявлен:

.

Нетрудно убедиться, что

.

Рассмотрим теперь решение задачи по определению характеристик работы страховой компании, основанное на распределении Пуассона.

Чтобы свести задачу к схеме Бернулли, заменим приближенно распределение следующей таблицей:

.

Здесь дисперсия

,

а среднее квадратичное отклонение обозначим через .

Затем в качестве денежной единицы примем условное математическое ожидание

руб.

С учетом последнего замечания вместо ряда распределения имеем:

.

Если число застрахованных равно , то общее число исков от застрахованных может рассматриваться как случайная пуассоновская величина с параметром , а средняя сумма исков застрахованных должна составлять

руб.

Предположим, что вероятность не разорения страховой кампании должна быть не менее , т. е. [46]

,

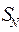где — капитал компании, а — суммарный иск застрахованных.

Очевидно, , где — квантиль уровня распределения Пуассона.

Таким образом, плата за страховку

руб.,

а относительная страховая надбавка должна составлять .

Однако наши рассуждения были бы верны, если бы ряды распределения и имели не только одинаковые математические ожидания _,но и дисперсии _, что в действительности не так.

Поэтому необходимо скорректировать полученные результаты. То есть, применяя схему Бернулли и используя при этом ряд распределения, необходимо в качестве параметра, описывающего рассеяние случайного иска, принять дисперсию, вычисленную по ряду распределения. Поскольку в полученные нами с использованием пуассоновского приближения результаты дисперсия случайного иска явно не входит, обоснуем алгоритм коррекции на основании центральной предельной теоремы.

Так как случайные иски 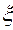, описываемые рядами, независимы и оди­на­ково распределены (напомним, что среднее квадратичное отклонение иска рав­но 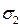), то при функция распределения нормированной суммы исков [1]

имеет предел, равный

,

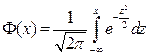и если мы хотим, чтобы вероятность не разорения компании была не менее , то цена страховки , нетто-премия и страховаянадбавка должны быть связаны соотношением [41]

,

где 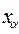— квантиль уровня стандартного гауссовского распределения.

Поэтому для вычисления основных характеристик работы страховой компании, если иски застрахованных имеют распределение (напомним, что среднее квадратичное отклонение иска равно ), необходимо в формулу внести поправочный коэффициент , т. е.

.

Очевидно, этот поправочный коэффициент [41]

.

Переходя опять к приближению Пуассона, отметим, что новая относительная страховая надбавка с учетом коррекции станет равной

,

а цена страхового полиса станет равной сумме нетто-премии 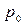и новой страховой надбавки [41]:

. (6)

Таким образом, в методических указаниях рассмотрен алгоритм вычисления основных характеристик работы страховой компании, при схеме краткосрочного страхования жизни, использующий распределение Пуассона. Итак, для нахождения «правильного» соотношения между величинами страховой выплаты, страховки и страховой надбавки можно использовать теперь как гауссовское, так и пуассоновское приближения.

Проиллюстрируем применение методики нахождения основных характеристик при данной схеме работы страховой компании следующим примером.

Пример. В страховой компании застраховано N1=3000 человек в возрасте 20 лет и N2=1000 человек в возрасте 40 лет сроком на один год. Компания выплачивает наследникам: 100000 руб., в случае смерти застрахованного от несчастного случая, и 25000 руб., в случае смерти от естественных причин в течение года. Компания не платит ничего, если человек проживет этот год. Предположив, что смертность описывается моделью Мейкхама, рассчитайте нетто-премию, цену полиса, страховую надбавку, чтобы вероятность не разорения компании составляла 0,95. Привести решения, основанные на пуассоновском и гауссовском распределениях.

Решение. Индивидуальные иски x и x каждого из застрахованных 1-ой и 2-ой групп определяются, соответственно, рядами распределения (для удобства за денежную единицу примем 100000 руб.).

0 1/4 1

x : (7)

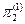=0,9982 =0,0013 =0,0005,

0 1/4 1

x : (8)

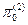=0,9962 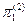=0,0033 =0,0005.

Здесь вероятности смерти в течение года от несчастного случая примем равными 0,0005, а вероятности смерти от естественных причин возьмем из Таблицы продолжительности жизни (см. стр.34 [ 46 ]). Средние индивидуальные иски М x и М x равны соответствующим нетто-премиям Р и Р для клиентов компании 1-ой и 2-ой групп.

Р = М x = ¼·0,0013 + 1·0,0005» 0,00083 = 83 руб., (9)

Р = М x = ¼·0,0033 + 1·0,0005» 0,00133 = 133 руб.

1°. Сначала рассмотрим решение, основанное на распределении Пуассона.

Чтобы свести задачу к схеме опытов Бернулли можно приближенно заменить ряды распределения (7) следующими таблицами:

0 М (x /x ¹ 0) 0 М (x /x ¹ 0)

x :, x :, (10)

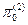
а затем в качестве условной денежной единицы принять условные математические ожидания М (x /x ¹0) в 1-ой таблице и М (x /x ¹0) – во 2-ой.

Вычислим условные математические ожидания:

М (x /x ¹0) = ¼· Р (x =¼/x ¹0) + 1· Р (x =1/x ¹0) = ¼· /() + 1· = ¼·0,0013/(0,0013+0,0005) + 1·0,0005/(0,0013+0,0005)= = ¼·13/18+1·5/18=33/72»0,458=45800 руб. – денежная единица для клиентов 1-ой группы.

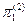М (x /x ¹0)=¼· /()+1· 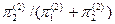=¼·0,0033/(0,0033+0,0005)+ +1·0,0005/(0,0033+0,0005) = ¼·33/38+1·5/38=53/152»0,349=34900руб.–денежная единица для клиентов 2-ой группы.

С учетом всех замечаний вместо рядов распределения (10) имеем:

x : 0 1 x : 0 1 (11)

0,9982 0,0018, 0,9962 0,0038

откуда получаем

М x = 0,0018, М x = 0,0038.

Подсчитаем сумму исков от застрахованных

1-ой группы:

l = М x = N₁· М x = 3000·0,0018 = 5,4,

2-ой группы:

l = М x = N₂ · М x = 1000·0,0038 = 3,8.

Общая сумма исков может рассматриваться, как случайная пуассоновская величина с параметром l +l = 9,2.

Так как вероятность не разорения компании должна быть не меньше 0,95, необходимо чтобы для общей суммы исков от застрахованных x = x + x выполнялось соотношение:

Р (x £ x) ³ 0,95,

где х – капитал компании.

Очевидно, что х = х 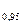, здесь х 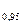»14 – квантиль уровня 0,95 для распределения Пуассона (см., например, таблицу 2 приложения 9 или таблицу на стр.49 [46]).

За счет нетто-премий компания может получить только сумму 9,2=5,4·45800руб.+3,8·34900руб.=247320руб.+132620руб.=379940руб.»380000руб.

Поэтому страховая надбавка компании должна составлять

R =(14-9,2)/9,2·100%»52,2%= 0,522·380000 руб.»198360руб., (12)

т.е. относительная страховая надбавка равна 52,2%, а капитал компании

х» 380000 руб. + 198360 руб. = 578360 руб. (13) Таким образом, индивидуальные страховые надбавки r и r , цены полисов Р и Р для каждого из клиентов 1-ой и 2-ой группы соответственно равны (они пропорциональны нетто-премиям):

r = 0,52·Р = 0,52·83 руб.» 43 руб.,

r = 0,52· Р = 0,52·133 руб.» 69 руб., (14)

Р = Р + r » 83 руб. + 43 руб. = 126 руб.,

Р = Р + r »133 руб. + 69 руб. = 202 руб.

2°. Теперь решим задачу с помощью гауссовского приближения. Среднее значение общего суммарного иска от застрахованных

x = М x + М x

с учетом средних индивидуальных исков (9) равно:

М x=N₁· M x +N₂· М x = 3000·0,00083+1000·0,00133=2,49+1,33»3,8=380000руб. (15)

Дисперсию x в виду независимости x и x вычислим по формуле:

x= D x + D x »3000·0,00058+1000·0,0007=1,74+0,7=2,44. (16)

Здесь

D x = М (x ) - М ²x =0,00058–(0,00083) »0,00058, (17)

D x = М (x ) - М x = 0,0007 – (0,00133) » 0,0007,

где с помощью рядов распределения (7) имеем:

М (x ) = 1/16·0,0013 + 1·0,0005» 0,00058, (18) М (x ) = 1/16·0,0033 +1·0,0005» 0,0007.

На основании центральной предельной теоремы функция распределения нормированной случайной величины:

S = (x - M x)/ ,

при N₁ + N₂® ¥ имеет предел [41]

F(x) = (1/ )· 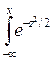dz.

Для гауссовского приближения случайной величины x верна следующая цепочка равенств:

Р (x < x) = Р ((x - М x)/ £ (х - М x)/ )» F((x - M x)/ ),

где х – капитал компании.

Для того чтобы вероятность не разорения компании не превосходила 0,95, т.е. F((x - M x)/ ) ³ 0,95 должно быть выполнено соотношение [41]

(х - M x)/ ³ х 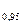, (19)

здесь х 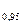» 1,645–квантиль уровня 0,95 стандартного гауссовского распределения.

Нетрудно убедиться в том, что минимально необходимый капитал компании должен составлять:

х= М x+х 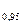· » 3,80+1,645·1,56=3,8+2,57=6,37=637000руб., (20)

а относительная страховая надбавка равна:

х 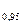· / М x·· 100%=2,57/3,8·100%»67,6%. (21)

Индивидуальные страховые надбавки r и r , цены полисов Р и Р для клиентов 1-ой и 2-ой групп с учетом (2), очевидно будут равны (страховые надбавки пропорциональны нетто-премиям):

r = 0,68·83 руб.» 56 руб.; (22)

r = 0,68·133 руб.» 90 руб.;

Р = Р + r »83 руб. + 56 руб. = 139 руб.;

Р = Р + r »133 руб. + 90 руб. = 223 руб.

3°. Проанализируем результаты, полученные в п. 1° и 2°. Очевидно расхождение результатов, полученных при использовании пуассоновского и гауссовского приближений. Попытаемся разобраться, в чем причина этого различия.

Дело в том, что при использовании закона Пуассона замена рядов распределения (7), (8) на ряды распределения (10) привела к тому, что не изменились лишь математические ожидания М x и М x . В то же время дисперсии D x и D x , свидетельствующие о степени рассеяния случайных индивидуальных исков x и x , найденные по рядам распределения (7), (8) и (10), различны. Следовательно, различны и дисперсии D x, найденные по рядам распределения (7), (8) и (10). Действительно, дисперсия общего суммарного иска x по рядам (7), (8) подсчитана: D x = 2,44 (см. соотношения (16)); вычислим теперь дисперсию x по рядам распределения (10), т.е.

0 0,458 0 0,349

x : x : (23)

0,9982 0,0018 0,9962 0,0038

Проведя расчеты, аналогичные (16)-(18), получим:

D x= 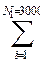D x + D x »3000·0,00038 + 1000·0,00046 = 1,6. (24)

Здесь:

D x = М (x ) - М x = 0,00038 – (0,00083) » 0,00038, (25)

D x = М (x ) - М x = 0,00046 – (0,00133) » 0,00046,

причем:

М (x ) = 0,458 ·0,0018» 0,00038, (26) М (x ) = 0,349 ·0,0038» 0,00046.

В дальнейшем будем использовать следующие обозначения: дисперсию x, найденную с использованием рядов (7), (8) обозначим s ,

а дисперсию x, найденную по рядам (10) или (23), обозначим s . Таким образом, s = 2,44, а s = 1,6.

Учитывая вышеизложенное, напрашивается естественный вывод: если относительная страховая надбавка, капитал компании, обеспечивающий не разорение компании с вероятностью 0,95, и цена полиса вычисляются, исходя из распределения суммарного иска застрахованных по закону Пуассона, то для нахождения основных характеристик компании необходимо ввести поправочный коэффициент, равный k = s₁ /s₂ (см.:(5) и [41]).

Проиллюстрируем применение коэффициента k для коррекции результатов, полученных в п.1°:

страховая надбавка с учетом (12) станет равной:

R =k·R = ·52,2%=1,235·52,2%» 64,5%» 245100 руб. (27) капитал компании (см.(13)) будет составлять:

х = 380000 руб. + 245100 руб.» 625100 руб., (28)

а индивидуальные: страховые надбавки и цены полисов (см.(14)):

r = k·r » 1,235·43 руб.» 53 руб.,

r = k·r » 1,235·69 руб.» 85 руб., (29)

Р = Р + r » 83 руб. + 53 руб. = 136 руб.,

Р = Р + r » 133 руб. + 85 руб. = 218 руб.

В заключение необходимо отметить, что характеристики работы компании, полученные с учетом коррекции результатов исследования, в котором суммарный иск застрахованных подчинен распределению Пуассона (см.(27)-(29)), хорошо согласуется с характеристиками работы страховой компании, которые получены, исходя из гауссовского приближения (см.(20)-(22)). Результаты исследования работы страховой компании, видимо, были бы еще более точны, если бы квантили уровня α распределения Пуассона можно было бы определить более точно.

Приложение 1

Линейная производственная задача
№1.1 45 60 21 14 3 6 3 0 180 6 2 0 6 210 2 3 5 7 112   №1.4. 30 11 45 6 3 2 6 0 150 4 2 3 5 130 4 3 2 4 124   №1.7. 35 41 22 12 2 2 3 4 151 3 1 0 2 156 1 4 4 0 162   №1.10. 59 27 20 35 1 3 2 2 102 3 2 0 3 204 4 2 3 1 188   №1.13. 34 32 28 36 2 4 5 3 128 3 0 4 1 130 3 5 0 2 142   №1.16. 27 10 9 8 3 5 0 6 144 2 0 1 0 130 1 4 2 3 140	№1.2 36 32 10 13 2 3 4 1 103 4 2 0 2 148 2 8 7 0 158   №1.5 48 30 29 10 3 2 4 3 198 2 3 1 2 96 6 5 1 0 228   №1.8. 38 12 28 21 3 0 3 3 186 2 3 1 1 102 4 3 2 2 196   №1.11. 30 28 9 23 1 0 2 5 110 3 6 0 4 126 2 4 1 3 114   №1.14. 27 39 18 20 2 1 6 5 140 0 3 0 4 90 3 2 4 0 198   №1.17. 31 10 14 20 1 4 3 4 120 3 0 2 2 168 2 5 0 3 80	№1.3. 48 15 11 32 4 2 3 1 116 2 0 3 2 94 4 1 0 5 196   №1.6. 28 14 11 20 4 2 2 4 112 2 3 1 0 32 1 4 0 2 46   №1.9. 60 12 44 17 4 2 4 1 180 4 0 2 2 160 2 4 3 0 109   №1.12. 16 18 14 12 4 3 0 6 192 0 1 5 0 24 1 2 4 3 90   №1.15. 24 20 31 10 3 0 2 5 162 3 6 0 3 134 2 4 3 1 148   №1.18. 34 20 8 23 2 0 2 3 142 1 5 4 2 100 3 4 0 1 122

№1.19 30 25 14 12 2 3 0 4 148 4 1 5 0 116 0 2 4 3 90   №1.22. 26 35 18 30 2 5 1 4 126 3 0 7 2 84 2 1 4 0 75   №1.25. 31 10 41 29 4 0 8 7 316 3 2 5 1 216 5 6 3 2 199   №1.28. 36 30 16 12 4 5 2 3 180 6 0 4 1 150 0 7 6 5 140   №1.31. 8 21 17 36 8 5 6 2 100 1 0 1 4 80 2 7 3 0 70   №1.34. 31 16 18 8 5 7 1 8 140 8 3 0 1 60 0 4 6 2 100

№1.20. 18 19 8 5 3 2 0 3 168 0 1 4 2 60 1 3 5 0 112   №1.23. 44 28 78 23 4 1 6 3 288 7 3 1 2 240 2 4 5 1 200   №1.26. 36 14 25 50 4 3 4 5 208 2 5 2 2 99 3 1 2 5 181   №1.29. 45 33 30 42 4 9 8 1 220 5 2 3 0 200 0 3 1 6 216   №1.32. 21 16 32 18 2 6 1 8 220 3 1 0 2 240 0 2 4 1 200   №1.35. 15 16 52 13 2 2 2 1 250 1 0 4 3 220 7 3 0 5 240

№1.21. 50 27 34 54 5 4 6 7 275 2 0 4 2 100 3 2 0 1 85   №1.24. 42 28 17 19 5 2 4 1 132 3 4 0 6 124 4 2 5 4 117   №1.27. 48 33 16 22 6 3 1 4 252 2 4 5 1 144 1 2 4 3 80   №1.30. 35 10 54 40 9 8 4 2 176 3 1 6 0 180 2 1 0 8 200   №1.33. 13 24 17 25 9 2 8 1 70 1 4 1 0 96 2 0 3 5 80   №1.36. 32 8 10 18 4 6 4 5 100 8 3 1 0 72 0 2 7 9 63

№1.37. 18 32 5 6 4 2 3 1 80 0 8 1 2 96 6 0 1 1 84   №1.40. 1 20 12 54 2 3 5 4 105 1 0 1 3 24 0 4 2 6 108   №1.43. 32 43 11 16 5 3 0 2 253 1 4 2 1 105 3 0 4 6 140   №1.46. 17 59 71 4 1 3 5 1 266 2 4 6 0 326 3 0 2 4 110   №1.49. 26 35 18 30 2 5 1 4 126 3 0 7 2 84 2 1 4 0 75   №1.52. 31 10 41 29 4 0 8 7 316 3 2 5 1 216 5 6 3 2 199

№1.38. 40 15 27 55 5 3 2 5 175 2 1 0 6 140 1 0 3 4 80   №1.41. 47 28 15 9 5 4 0 1 181 3 5 2 6 165 2 0 3 1 50   №1.44. 6 30 106 54 1 3 5 4 231 2 4 0 3 84 0 1 6 3 224   №1.47. 25 26 28 80 1 3 4 2 202 2 1 0 6 318 3 0 5 1 211   №1.50. 44 28 78 23 4 1 6 3 288 7 3 1 2 240 2 4 5 1 200   №1.53. 36 14 25 50 4 3 4 5 208 2 5 0 2 99 3 1 2 5 181

№1.39. 6 32 25 68 3 4 1 5 142 5 1 0 2 63 0 2 3 6 106   №1.42. 17 80 48 33 1 6 2 4 186 0 5 6 1 259 2 4 0 3 68   №1.45. 54 20 21 45 3 2 1 4 257 2 1 0 5 215 6 3 4 0 210   №1.48. 50 27 34 54 5 4 6 7 275 2 0 4 2 100 3 2 0 1 85   №1.51. 42 28 17 19 5 2 4 1 132 3 4 0 6 124 4 2 5 4 117   №1.54. 48 33 16 22 6 3 1 4 252 2 4 5 1 144 1 2 4 3 80

Приложение 2

Транспортная задача линейного программирования

Приложение 3

Нелинейная задача распределения ресурсов.

Дата добавления: 2015-06-04