Глубина изображаемого пространства

Глубиной изображаемого пространства называется измеренное вдоль оптической оси расстояние между точками пространства предметов, определяющим границы его резкого изображения оп­тической системой в данной плоскости. Различают глубину в про­странстве предметов (глубина изображаемого пространства) и глубину в пространстве изображений (глубина резкости). В осно­ве их лежат одинаковые представления, а именно: способность глаза человека видеть изображения, образованные кружками рас­сеяния, в виде резких точечных изображений.

Рассмотрим оптическую систему, изображенную в виде зрач­ков входа и выхода (рис. 4.10.1).

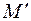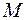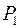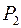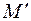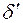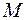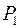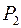Допустим, что плоскость оптически сопряжена с плоско­стью . Точки и проектируются на плоскость изображения в виде кружков рассеяния . Если глаз человека, имеющий определенную разрешающую способность, не сможет увидеть кружки рассеяния из-за их малости, то вместе с предметами, расположенными в плоскости , он будет видеть резко точки и . Глубина в пространстве предметов определяется формулой

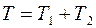(4.10.1)

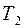где - передняя глубина, -задняя глубина. Плоскость 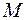называется плоскостью наводки.

Из подобия треугольников и 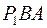имеем:

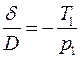
Заменяя 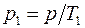и преобразуя, получим:

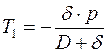(4.10.2)

Аналогичным образом найдем заднюю глубину

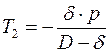(4.10.3)

Кружки рассеяния 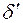видны, если их угловые размеры превос­ходят разрешающую силу глаза. Кружку рассеяния 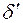соответ­ствует в плоскости предметов 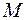кружок рассеяния 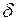. Между 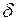и 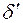для случая бесконечно удаленных предметов существует про­стая зависимость:

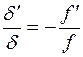
Если разрешающую силу в угловой мере обозначим через 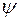, то 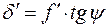и последнее выражение примет вид:

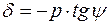
Подставляя это равенство в формулу (4.10.2) и (4.10.3), получим:

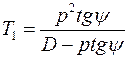(4.10.4)

и

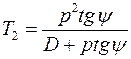(4.10.5)

Подставляя в (31,1), получим:

(4.10.6)

Найдем такое положение плоскости наводки, начиная с которого и далее от оптической системы все предметы изображаются рез­ко, т. е. 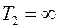. Для этого необходимо, чтобы:

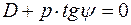или 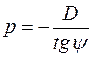(4.10.7)

Определим переднюю глубину для такого положения плоско­сти предметов. Подставим в (4.10.4):

или

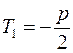(4.10.8)

Найденное расстояние до плоскости наводки 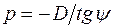, при котором задняя глубина 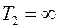называется гиперфокальным фо­кусным расстоянием. В этом случае все предметы, расположенные от объектива на расстоянии от 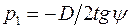до бесконечности, изображаются в плоскости изображения резко. Расстояние 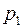и следует именовать «началам бесконечности».

Преобразуем формулы (4.10.2) и (4.10.3), заменив в них величи­ны 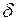и 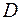следующими выражениями:

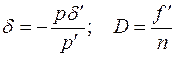
Тогда:

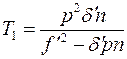(4.10.9)

и

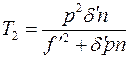(4.10.10)

Мы получили рабочие формулы для расчета глубины изображае­мого пространства.

Пример. Найти глубину изображаемого пространства для фотографического объектива с фокусным расстоянием 50 мм и от­носительным отверстием 1: 3,5 при наводке на плоскость, распо­ложенную от объектива на расстоянии 5 м, если разрешающая способность объектива 25 штр/мм.

Решение. Дано: 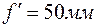; ; 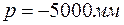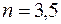. Данной разрешающей способности в линейной мере соответствует 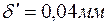. Применив формулы (4.10.9) и (4.10.10), получим:

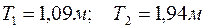
и полная глубина:

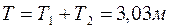
Дата добавления: 2015-06-04