Эквипотенциальные поверхности

Связь между напряженностью и потенциалом.

Для потенциального поля, между потенциальной (консервативной) силой и потенциальной энергией существует связь

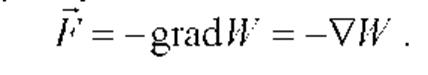
где 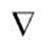("набла") - оператор Гамильтона.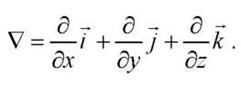

Поскольку 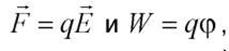то

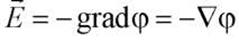
Знак минус показывает, что вектор Е направлен в сторону убывания потенциала.

Для графического изображения распределения потенциала используются эквипотенциальные поверхности - поверхности во всех точках которых потенциал имеет одно и то же значение.

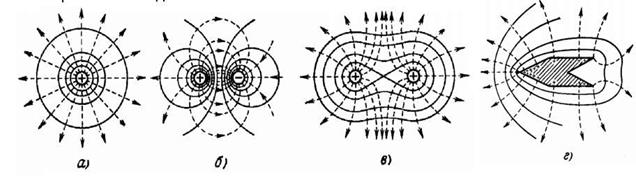
Эквипотенциальные поверхности обычно проводят так, чтобы разности потенциалов между двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше. На рисунке пунктиром изображены силовые линии, сплошными линиями - сечения эквипотенциальных поверхностей для: положительного точечного заряда (а), диполя (б), двух одноименных зарядов (в), заряженного металлического проводника сложной конфигурации (г).

Для точечного заряда потенциал 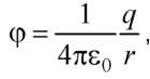поэтому эквипотенциальные поверхности - концентрические сферы. С другой стороны, линии напряженности - радиальные прямые. Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям.

Можно показать, что во всех случаях вектор Е перпендикулярен эквипотенциальным поверхностям и всегда направлен в сторону убывания потенциала.

Примеры расчета наиболее важных симметричных электростатических полей в вакууме.

1. Электростатическое поле электрического диполя в вакууме.

Электрическим диполем (или двойным электрическим полюсом) называется система двух равных по модулю разноименных точечных зарядов (+q,-q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля (l<< r).

Плечо диполя l - вектор, направленный по оси диполя от отрицательного заряда к положительному и равный расстоянию между ними.

Электрический момент диполя ре - вектор, совпадающий по направлению с плечом диполя и равный произведению модуля заряда |q| на плечо I: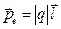

1) Напряженность поля диполя на продолжении оси диполя в точке А

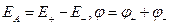Пусть r - расстояние до точки А от середины оси диполя. Тогда, учитывая что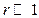

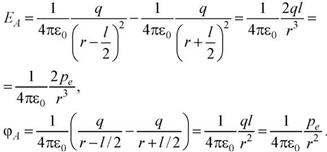
2)Напряженность поля в точке В на перпендикуляре, восстановленном к оси диполя из его середины при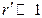

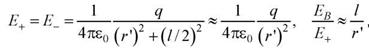поэтому

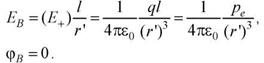
Точка В равноудалена от зарядов +q и -q диполя, поэтому потенциал поля в точке В равен нулю. Вектор Ёв направлен противоположно вектору l.

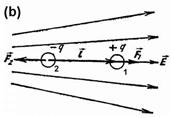
3)Во внешнем электрическом поле на концы диполя действует пара сил, которая стремится повернуть диполь таким образом, чтобы электрический момент ре диполя развернулся вдоль направления поля Ё (рис.(а)).

Во внешнем однородном поле момент пары сил равен M = qElsin а или 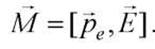Во внешнем неоднородном поле (рис.(в)) силы, действующие на концы диполя, неодинаковы 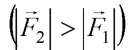и их результирующая стремится передвинуть диполь в область поля с большей напряженностью - диполь втягивается в область более сильного поля.

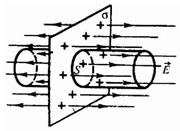
2. Поле равномерно заряженной бесконечной плоскости.

Бесконечная плоскость заряжена с постоянной поверхностной плотностью 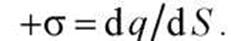Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны.

В качестве Гауссовой поверхности примем поверхность цилиндра, образующие которого перпендикулярны заряженной плоскости, а основания параллельны заряженной плоскости и лежат по разные стороны от нее на одинаковых расстояниях.

Так как образующие цилиндра параллельны линиям напряженности, то поток вектора напряженности через боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания 2ES. Заряд, заключенный внутри цилиндра, равен 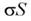. По теореме Гаусса 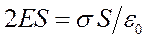откуда: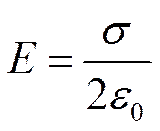

Е не зависит от длины цилиндра, т.е. напряженность поля на любых расстояниях одинакова по модулю. Такое поле называется однородным.

Разность потенциалов между точками, лежащими на расстояниях х1 и х2 от плоскости, равна

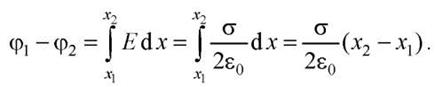
3.Поле двух бесконечных параллельных разноименно заряженных плоскостей с равными по абсолютному значению поверхностными плотностями зарядов σ>0 и - σ.

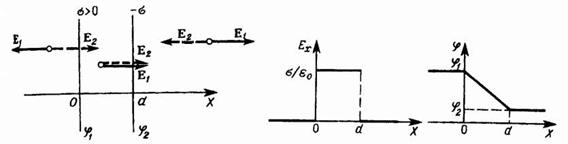
Из предыдущего примера следует, что векторы напряженности Е₁ и E₂ первой и второй плоскостей равны по модулю и всюду направлены перпендикулярно плоскостям. Поэтому в пространстве вне плоскостей они компенсируют друг друга, а в пространстве между плоскостями суммарная напряженность 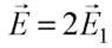. Поэтому между плоскостями

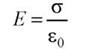(в диэлектрике. ).

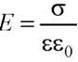Поле между плоскостями однородное. Разность потенциалов между плоскостями.
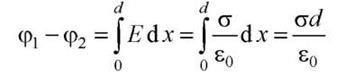(в диэлектрике ).

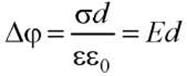4.Поле равномерно заряженной сферической поверхности.

Сферическая поверхность радиуса R с общим зарядом q заряжена равномерно с поверхностной плотностью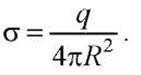

Поскольку система зарядов и, следовательно, само поле центрально-симметрично относительно центра сферы, то линии напряженности направлены радиально.

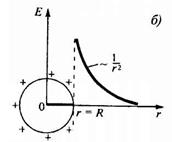
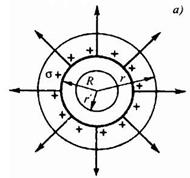В качестве Гауссовой поверхности выберем сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд q. По теореме Гаусса 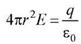, откуда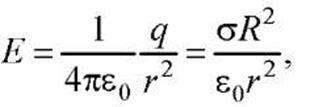

При r<=R замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферы Е = 0.

Разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра сферы

(r1 >R,r2 >R), равна

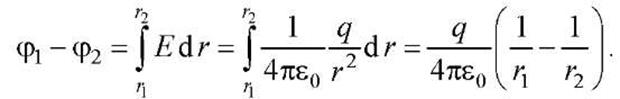
Вне заряженной сферы поле такое же, как поле точечного заряда q, находящегося в центре сферы. Внутри заряженной сферы поля нет, поэтому потенциал всюду одинаков и такой же, как на поверхности

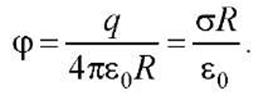
5. Поле объемно заряженного шара.

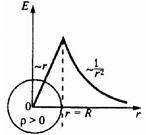Заряд q равномерно распределен в вакууме по объему шара радиуса R с объемной плотностью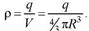

Центр шара является центром симметрии поля.

1) Для поля вне шара (г > R) получаем тот же результат, что и в случае сферической поверхности

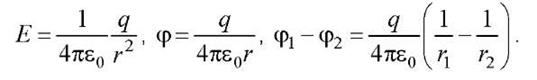
2)При r= R

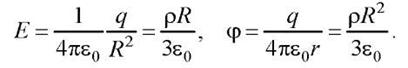
3)Внутри шара сфера радиусом r<R охватывает заряд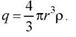

По теореме Гаусса

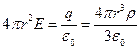
Отсюда, для точек, лежащих внутри шара r1<R, r2<R), с учетом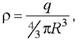

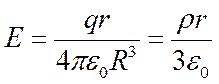
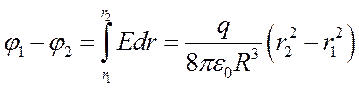
6. Поле равномерно заряженного бесконечного цилиндра (нити).

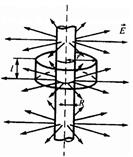Бесконечный цилиндр радиуса R заряжен равномерно с линейной плотностью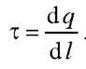

Линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра.

В качестве Гауссовой поверхности выберем цилиндр радиуса г и высотой I коаксиальный с заряженной нитью.

Торцы этого цилиндра параллельны линиям напряженности, поэтому поток через них равен нулю.

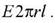. Поток через боковую поверхность равен

По теореме Гаусса (при r>R) 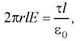откуда при r1>R, r2 >R

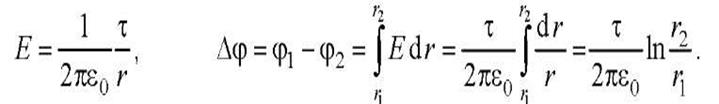
Если г <R, то замкнутая поверхность зарядов внутри не содержит, поэтому Е=0.

Дата добавления: 2015-06-04