Энергия электростатического поля

Энергия заряженного конденсатора.

Элементарная работа внешних сил по перенесению малого заряда dq с обкладки 2 конденсатора на обкладку 1

Работа внешних сил при увеличении заряда конденсатора от 0 до q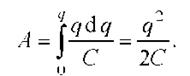

Энергия заряженного конденсатора (используя )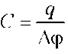

В общем случае электрическую энергию любой системы заряженных неподвижных тел - проводников и непроводников - можно найти по формуле

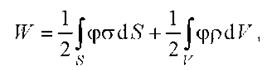
где σ и ρ- поверхностная и объемная плотности свободных зарядов; ср - потенциал результирующего поля всех свободных и связанных зарядов в точках малых элементов dS и dV заряженных поверхностей и объемов. Интегрирование проводится по всем заряженным поверхностям S и по всему заряженному объему V тел системы.

На примере поля плоского конденсатора выразим энергию поля через его напряженность. Для конденсатора 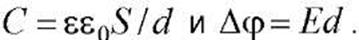Отсюда

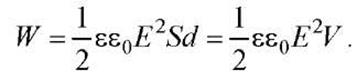
В однородном поле конденсатора его энергия распределена равномерно по всему объему поля V = Sd.

Объемная плотность энергии электростатического поля плоского конденсатора w

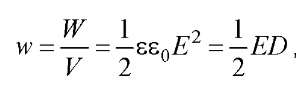
Где 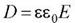- электрическое смещение.

Эта формула является отражением того факта, что электростатическая энергия сосредоточена в электростатическом поле. Это выражение справедливо также и для неоднородных полей.

Пондеромоторные силы.

Механические силы, действующие на заряженные тела, помещенные в электромагнитное поле, называются пондеромоторными силами (от латинских слов ponderis - тяжесть и motor - движущий).

Например, в плоском конденсаторе сила, с которой пластины конденсатора притягивают друг друга, совершает работу за счет уменьшения потенциальной энергии системы. С учетом 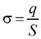и 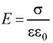, получаем

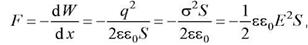
где знак минус указывает на то, что эта сила является силой притяжения. Под действием этой силы обкладки конденсатора сжимают пластину диэлектрика, помещенного между ними, и в диэлектрике возникает давление

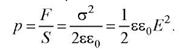
Задача №1. Четыре одинаковых положительных точечных заряда величиной q_i = 3,3·10^-9 Клзакреплены в вершинах квадрата со стороной0,1 м. Найти силу, действующую со стороны трех зарядов на четвертый.

qi = 3,3·10^-9 Кл; а = 0,1 м.
F –?

Решение: сила, действующая на заряд q₄ со стороны трех зарядов q₁, q₂ и q₃, равна:

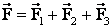
Учитывая, что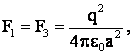

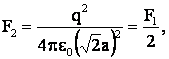
F ≈ 2·10^-5 H.

Ответ: сила, действующая на четвёртый заряд равна F ≈ 2·10^-5 H.

Задача №2. Два точечных отрицательных заряда q₁ и q₂ находятся на расстоянии ℓ друг от друга. Где надо поместить третий точечный зарядq₃,чтобы все три заряда оказались в равновесии? Какова должна быть величина и знак заряда q₃?

Решение: заряд q₃ должен находиться между зарядами q₁ и q₂ на прямой, их соединяющей, поскольку только в этом случае силы F₃₁ и F₃₂, с которыми на заряд q₃ действуют заряды q₁ и q₂ будут располагаться на одной прямой и иметь противоположные направления, что необходимо для равновесия. Силы, действующие на каждый из зарядов q₁ и q₂ со стороны двух других зарядов, будут уравновешены, если знак заряда q₃ будет положительным.

Пусть заряд q₃ находится на расстоянии x₀ от заряда q₁. Запишем условие равновесия заряда q₃, к которому приложены силы F₃₁ и F₃₂:

F₃₁ = F₃₂ (1)

Подставим в уравнение (1) вместо сил их значения по закону Кулона

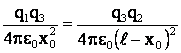
Найдем два значения искомого расстояния x :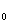

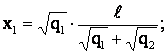
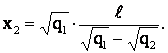
Отбросим корень x₂, поскольку при этом заряд q 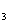находится не между зарядами q₁ и q₂, что невозможно для его равновесия.

Следовательно искомое расстояние x₀ равно:

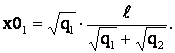(2)

Чтобы найти величину заряда q₃, запишем условие равновесия одного из двух зарядов q₁ или q₂, например q₁:

F₁₂ = F₃₁.

Поставим вместо сил их значения по закону Кулона и получим:

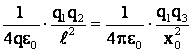
Заменим величину x₀ ее значением по формуле (2) и получим:

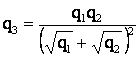
Ответ: знак заряда q₃ отрицателен и равен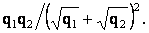

Задача №3. Два одинаковых маленьких шарика массой m = 0,4 г каждый подвешены на непроводящих нитях длиной ℓ = 1 м к одной точке. После того как шарикам были сообщены одинаковые заряды q,они разошлись на расстояние r = 9 см. Определить заряды шариков и силу натяжения нити. Диэлектрическая проницаемость воздуха ε = 1.

m1 = m2 = m = 0,4 г = 4·10^-4 кг; r = 9 cм = 9·10^-2 м; ε = 1; ℓ1 = ℓ2 = ℓ = 1 м.
q, Т –?

Решение: на каждый шарик (рис.) действуют следующие силы: сила тяжести 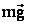, сила натяжения нити 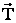и сила взаимодействия 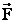Шарик находится в равновесии. Следовательно, выполняется условие:

,

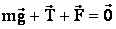поэтому суммы проекций сил на оси ОХ и ОУ равны нулю:

F – Tsinα = 0,

Tcosα – mg = 0,

или Tsinα = F,

Tcosα = mg (1)

Разделив равенства (1) почленно первое на второе, получим:

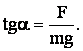
Так как угол α мал то 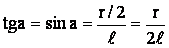, поэтому:

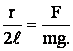(2)

По закону Кулона: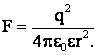

Подставим это выражение в равенство (2):

,

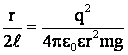откуда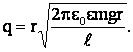

Из уравнения (1) найдем модуль силы натяжения нити:

,

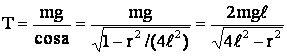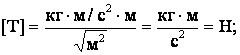
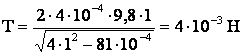
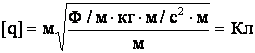
Ответ: заряды имели величину по 1·10^-8 Кл, сила натяжения нити 4·10^-3 Н.

Задача №4. В двух вершинах при основании прямоугольного равнобедренного треугольника расположены точечные заряды q₁ = q₂ = 2·10^-8Кл. Расстояние между зарядами 0,6 м. Найти напряженность и потенциал электрического поля в третьей вершине треугольника, а также по середине между зарядами.

q1 = q2 = q = 2·10^-^8 Кл; ε = 1; ℓ = 0,6 м.
Еа, φа, Ев, φв –?

Решение: направления векторов напряженностей в точке А и В показаны на чертеже (рис.). Напряженности и потенциалы в точке А от каждого заряда, удаленного от точки А на 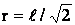, равны:

;

.

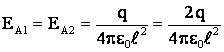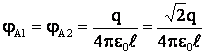Тогда для результирующего поля в точке А:

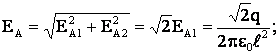
Е_А ≈ 1,4·10³ Н/Кл.

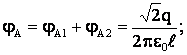
φ_А ≈ 840 В.

Векторы напряженности в точке В от каждого заряда равны и противоположны, а потенциалы от каждого заряда:

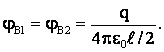
Поэтому для суммарного поля в точке В:

Е_в = 0;

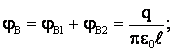
φ_в ≈ 1200 В

Ответ: согласно рисунка для точек А и В: φ_А = 840 В; Е_А = 1,4·10³ Н/Кл; φ_в = 1200 В; Е_в = 0

Задача №5. В вертикальном однородном электрическом поле напряженностью Е = 600 В/см находится в равновесии капелька ртути. Заряд капли равен 0,8·10^-19 Кл. Найти радиус капли. Плотность ртути 1,36·10⁴ кг/м³.

q = 0,8·10^-19 Кл; Е = 600 В/см; ρ = 1,36·10^4 кг/м^3.
r –?

Решение: на капельку ртути действуют сила тяжести mg и электрическая сила F (рис.). По условию равновесия в проекции на вертикаль mg – F = 0.

Масса шарика: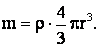

Из этих уравнений с учетом, что F = qE, получим:

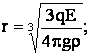
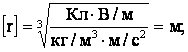
Ответ: радиус капли 4,4·10^-7 м.

Задача №6. Положительно заряженный металлический шар (рис.) создает поле, напряженность которого в точке А Е_А = 100 В/м, а в точке С – Е_с = 36 В/м. Какова напряженность поля в точке В, лежащей посередине между точками А и С? Шар находится в воздухе.

ЕА = 100 В/м; Еc = 36 В/м; ε = 1; ε = 8,85·10^-12 Ф/.
Ев –?

Решение: обозначим расстояние от центра шара О до точек А, В и С через r₁, r₂ и r₃ соответственно. Тогда напряженность поля в точке В:

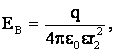(1)

где q – заряд шара.

Учитывая, что АВ = ВС, найдем:

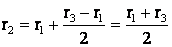(2)

Напряженности поля в точках А и С равны соответственно:

,

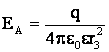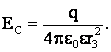
Выразим отсюда расстояния r₁ и r₃:

,

.

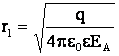Учитывая эти значения, по формуле (2) находим:

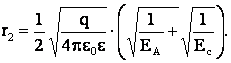(3)

Подставим значение (3) в формулу (1), получим после преобразований и вычислений:

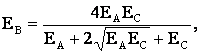
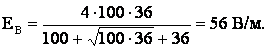
Ответ: напряженность в т. В равна 56 В/м.

Задача №7. Поле образовано зарядом q₁ = 166,7·10^-9 Кл. Какую работу надо совершить, чтобы одноименный заряд q₂ = 3,3·10^-9 Кл перенести из точки, удаленной от первого заряда на 50 см в точку, удаленную от первого заряда на 5 см?

q1 = 166,7·10^-9 Кл; q2 = 3,3·10^-9 Кл; r1 = 50 см = 0,5 м; r2 = 5 см = 0,05 м.
А1 –?

Решение: пусть заряд q₂ перемещается из точки В в точку С в электрическом поле, созданном точечным зарядом q₁ (рис.). Работа сил поля:

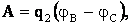
где φ_в, φ_А – потенциалы поля, образованного точечным зарядом q₁ в точках В и С:

,

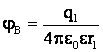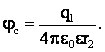
Из этих уравнений: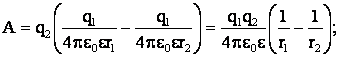

А = –9·10^-5 Дж.

Знак минус означает, что электрическая сила направлена в сторону, противоположную движению. Для перемещения заряда к нему должна быть приложена внешняя сила, направленная по движению, работа которой А₁ = –А.

Ответ: надо совершить работу А₁ = –9·10^-5 Дж.

Задача №8. Найти скорость электрона, прошедшего разность потенциалов, равную 10³ B. Начальная скорость равна нулю.

U = 10³ B; m = 9,1·10^-31 Кг; e = –1,6·10^-19 Кл; U₀ = 0.

v –?

Решение: работа сил поля идет на увеличение кинетической энергии электрона:

А = ∆Е_к,

где А = |e|U,

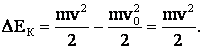
Из этих зависимостей: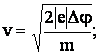

v = 1,87·10⁷ м/с.

Ответ: электрон получает скорость 1,87·10⁷ м/с.

Задача №9. Электрон движется по направлению силовой линии однородного электрического поля из точки, потенциал которой 10⁴ В. Как долго движется электрон в поле до полной потери скорости, если его начальная скорость 3·10⁷ м/с, а перемещение электрона до полной остановки 5·10^-3 м? Определить потенциал точки, в которой скорость электрона станет равной нулю. Найти отношение силы тяжести электрона к силе, действующей на него со стороны поля.

φ1 = 10^4 В; v0 = 3·10^7 м/с; v = 0; S = 5·10^-3 м; q = –1,6·10^-19 Кл; m = 9,1·10^-31 кг.
φ2, t, n –?

Решение: на электрон действует сила со стороны электрического поля 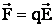(рис.). Поскольку поле однородное, то 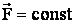, и движение электрона является равнозамедленным. Уравнения кинематики:

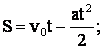
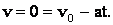
Из этих уравнений: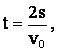

t = 3,3·10^-10 c.

Работа поля равна изменению кинетической энергии электрона:

A = ∆Е_к

Так как: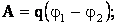

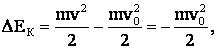то

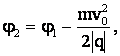
φ₂ = 7,4·10³ В.

Из этих формул с учетом равенства 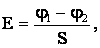найдем требуемое отношение сил:

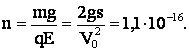
Ответ: потенциал точки, в которой скорость электрона равна нулю, 7,4·10³ В. Отношение mg/F равно 1,1·10^-16.

Задача №10. 1000 одинаковых заряженных шарообразных капель воды имеют одинаковый потенциал 10^-2 В. Определить потенциал большой капли, получившейся в результате слияния малых капель.

φ = 10^-2 В; N = 1000.

φ₀ –?

Решение: потенциалы большой φ₀ и одной малой капель:

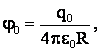
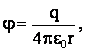
где R, q₀ – радиус и заряд большой капли,

r, q – радиус и заряд малой капли.

При слиянии N малых капель заряд большой капли:

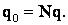
Объем большой капли равен сумме объемов малых капель:

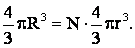
Из этих уравнений найдем:

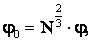
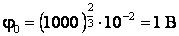
Ответ: потенциал большой капли 1 В.

Задача №11. Шар радиусом 5·10^-2 м имеет заряд 6·10^-8 Кл, шар радиусом 1·10^-1 м и имеет такой же заряд. Шары соединяют проволокой. Какое количество электричества переместится с одного шара на другой.

r₁ = 5·10^-2 м; r₂ = 1·10^-1 м; q = 6·10^-8 Кл; ε = 1.

∆q –?

Решение: у шаров одинаковые заряды, но потенциалы разные: большой шар, т.е. с большой емкостью, имеет меньший потенциал. Под действием разности потенциалов заряды будут перетекать по проволоке в направлении от меньшего шара к большему. Это перетекание будет происходить до тех пор, пока потенциалы обоих шаров не выравниваются до одного значения φ. Заряд первого малого шара уменьшится на величину ∆q и будет равен 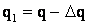; заряд второго шара увеличится на ту же величину ∆q и станет равным 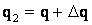. Потенциал шаров после соединения:

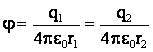или .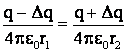

Отсюда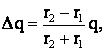

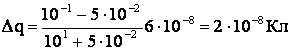
Ответ: заряд перемещается в 2·10^-8 Кл с меньшего шара на больший.

Задача №12. Плоский воздушный конденсатор зарядили при помощи источника с напряжением U₁ = 200 В. Затем конденсатор был отключен от источника. Каким станет напряжение между пластинами, если расстояние между ними увеличить от d₁ = 0,2 мм до d₂ = 0,7 мм, а пространство между пластинами заполнить слюдой (ε₂ = 7).

U₁ = 200 В; d₁ = 0,2 мм = 0,2·10^-3 м; d₂ = 0,7 мм = 0,7·10^-3 м; ε₁ = 1; ε₂ = 7.

U₂ –?

Решение: емкость конденсатора и напряжение на нем до раздвижения пластин равны:

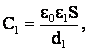
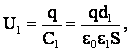(1)

а после раздвижения: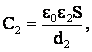

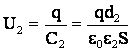(2)

Так как конденсатор перед раздвижением был отключен от источника напряжения, то заряд на пластинах конденсатора q не изменяется. Поэтому разделив почленно выражение (1) на (2), получим

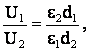
откуда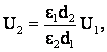

U₂ = 100 В.

Ответ: напряжение уменьшится до 100 В.

Задача №13. Обкладки конденсатора с неизвестной емкостью С₁, заряженного до напряжения U₁ = ∆φ₁ = 80 В, соединяют с обкладками конденсатора емкостью C₂ = 60 мкФ, заряженного до U₂ = ∆φ₂ = 16 В. Определить емкость С₁, если напряжение на конденсаторах после их соединения U = 20 B. Конденсаторы соединяются обкладками, имеющими:

а) одноименные заряды;

б) разноименные заряды.

U1 = ∆φ1 = 80 В; U2 = ∆φ2 = 16 В; C2 = 60 мкФ; U = 20 B.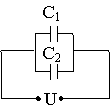
С1а, С1б –?

Решение: заряды на каждом конденсаторе до соединения равны:

q₁ = C₁·U₁,

q₂ = C₂·U₂.

Емкость системы конденсаторов после соединения:

C = C₁ + C₂,

суммарный заряд: q = UC = U·(C₁ + C₂).

Суммарный заряд системы должен равняться сумме зарядов на конденсаторах до соединения.

Следовательно:

1) для случая a: q₁ + q₂ = q или C₁U₁ + C₂U₂ = (C₁ + C₂)·U,

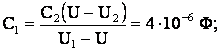
2) для случая б: q₁ – q₂ = q или C₁U₁ – C₂U₂ = (C₁ + C₂)·U,

Ответ: а) С₁ = 4 мкФ, б) С₂ = 36 мкФ.

Задача №14. Однородное электростатическое поле, напряженность которого Е = 1·10⁴ В/м, образовано двумя заряженными параллельными пластинами, расположенными на расстоянии d = 2 см друг от друга в воздухе. Какова разность потенциалов между пластинами? Чему будет равна разность потенциалов, если между пластинами параллельно им поместить металлический лист толщиной d₁ = 2 см?

Е = 1·10^4 В/м; d = 2 см = 2·10^-2 м; d1 = 5 см = 5·10^-2 м; ε = 1.
U1 –?

Решение: воспользуемся формулой, устанавливающей связь между напряженностью Е однородного электрического поля и разностью потенциалов U:

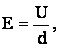
отсюда U = Ed. (1)

Если между пластинами параллельно им поместить металлический лист толщиной d₁ (рис. а), это приведет к образованию двух последовательно соединенных конденсаторов с расстояниями между обкладками d₂ и d₃ (рис. б). Емкости этих конденсаторов:

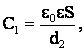
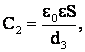(2)

где S – площадь одной пластины.

Пусть С – их общая емкость при последовательном соединении. Тогда:

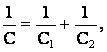
откуда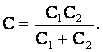

Подставляя сюда значения (2) и учитывая, что d₂ + d₃ = d – d₁, получаем:

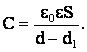(3)

Обозначим через С₀ емкость конденсатора, образованного двумя заряженными пластинами до внесения металлического листа. Заряд конденсатора до и после внесения листа один и тот же, так как конденсатор отключен от источника тока. Поэтому q = C₀·U = C·U₁.

Отсюда: 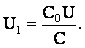(4)

Подставив в формулу (4) 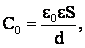а также значения (1) и (3), после очевидных преобразований получим:

U₁ = E·(d – d₁). (5)

U₁ = 2·10² В/м.

Формулы (3) и (5) показывают, что ведение проводящей пластины толщиной d₁, между обкладками конденсатора эквивалентно уменьшению расстояния между обкладками на эту толщину. В отключенном от источника тока конденсаторе это приводит к уменьшению разности потенциалов между обкладками.

Задача №15. Найти емкость батареи конденсаторов, соединенных по схеме, приведенной на рис. а. Все конденсаторы имеют одинаковую емкость С = 11 мкФ.

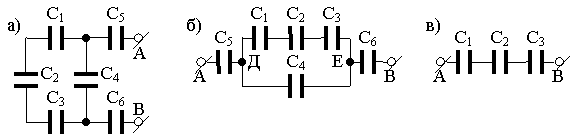
Решение: на рис. б изображена схема, эквивалентная данной схеме. Конденсаторы С₁, С₂ и С₃ соединены последовательно. Их общая емкость С′ = С/3. Параллельно этой цепи подключен конденсатор С₄. Значит, емкость цепи между точками D и Е:

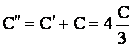
Теперь имеем схему, изображенную на рис. в. Емкость этой батареи С_б найдем из формулы для последовательного соединения конденсаторов:

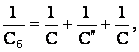
откуда

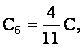
С_б = 4 мкФ.

Задача №16. Конденсаторы емкостями С, 2С и С_х соединены по схеме, приведенной на рис. Емкость батареи не изменяется при замыкании ключа К. Определить емкость С_х.

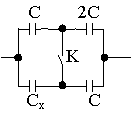
Решение: найдем сначала емкость батареи при разомкнутом ключе. Если соединены последовательно два конденсатора емкостями С₁ и С₂, то их общая емкость:

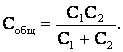
Воспользуемся этой формулой и найдем, что при разомкнутом ключе емкость верхней ветви, состоящей из последовательно соединенных конденсаторов емкостями С и 2С, равна:

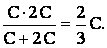
Емкость нижней ветви, состоящей из последовательно соединенных конденсаторов емкостями C_x и C равна:

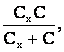
Верхняя и нижняя ветви соединены между собой параллельно. Поэтому емкость батареи:

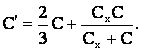(1)

При замкнутом ключе конденсаторы емкостями C и C_x соединены параллельно; их общая емкость равна;

C + C_x.

Конденсаторы емкостями 2C и C тоже соединены параллельно; их общая емкость равна:

2C + C = 3C.

Ветви, емкости которых C + C_x и 3C соединены последовательно. Значит, при замкнутом ключе емкость батареи:

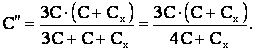(2)

По условию C′ = C″, поэтому на основании формул (1) и (2)

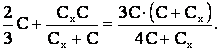
Решив это уравнение относительно С_х получим значение искомой емкости:

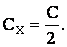
Задача №17. Пространство между пластинами плоского конденсатора заполнено диэлектриком. При некоторой разности потенциалов между пластинами энергия конденсатора W = 2·10^-5 Дж. После того как конденсатор отключили от источника напряжения, диэлектрик из конденсатора вынули. При этом против сил электростатического поля надо было совершить работу А = 7·10^-5 Дж. Найти диэлектрическую проницаемость диэлектрика.

W = 2·10^-5 Дж; А = 7·10^-5 Дж.

ε –?

Решение: пусть q – заряд конденсатора, C – его емкость при наличии диэлектрика между пластинами. Тогда энергия заряженного конденсатора:

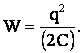
После того как вынули диэлектрик, емкость конденсатора уменьшилась в ε раз:

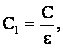
заряд остался прежним, а энергия приняла значение:

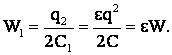
Изменение энергии равно работе внешних сил:

W₁ – W = A или εW – W = A,

отсюда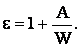

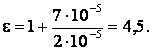
Ответ: диэлектрическая проницаемость диэлектрика 4,5.

Дата добавления: 2015-06-04