Стандартная форма линейных оптимизационных моделей 1 страница

Линейные оптимизационные модели можно решать с помощью графического и аналитического способов решения. Использование графического способа удобно только при решении задач ЛП с двумя переменными. При большем числе переменных необходимо применение аналитического аппарата. Рассмотрим общий метод решения задач ЛП, называемый симплекс – методом.

Информация, которую можно получить с помощью симплекс – метода, не ограничивается лишь оптимальными значениями переменных. Симплекс – метод фактически позволяет дать экономическую интерпретацию полученного решения и провести анализ модели на чувствительность.

Процесс решения задачи ЛП симплекс – методом носит итерационный характер: однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор, пока не будет получено оптимальное решение. Процедуры, реализуемые в рамках симплекс – метода, требуют применения ЭВМ – мощного средства решения задач ЛП.

Симплекс – метод – это характерный пример итерационных вычислений, используемых при решении большинства оптимизационных задач.

Выше было показано, что правая и левая части ограничений линейной модели могут быть связаны знаками £, = и ³. Кроме того, переменные, фигурирующие в задачах ЛП, могут быть неотрицательными или не иметь ограничения в знаке. Для построения общего метода решения задач ЛП соответствующие модели должны быть представлены в некоторой форме, которую назовем стандартной формой линейных оптимизационных моделей. При стандартной форме линейной модели

1. все ограничения записываются в виде равенств с неотрицательной правой частью;

2. значения всех переменных модели неотрицательны;

3. целевая функция подлежит максимизации или минимизации.

Покажем, каким образом любую линейную модель можно привести к стандартной.

Ограничения

1. Исходное ограничение, записанное в виде неравенства типа £ (³), можно представить в виде равенства, прибавляя остаточную переменную к левой части ограничения (вычитая избыточную переменную из левой части).

Например, в левую часть исходного ограничения

х₁ + 2х₂ £ 6 вводится остаточная переменная S₁>0, в результате чего исходное неравенство обращается в равенство

х₁ + 2х₂ + S₁=0; S₁³0

Если исходное ограничение определяет расход некоторого ресурса, переменную S₁ следует интерпретировать как остаток, или неиспользованную часть, данного ресурса.

Рассмотрим исходное ограничение другого типа:

3х₁ + 2х₂ –3х₃ ³ 5

Т.к. левая часть этого ограничения не может быть меньше правой, для обращения исходного неравенства в равенство вычтем из его левой части избыточную переменную S₂ >0. В результате получим

3х₁ + 2х₂ –3х₃- S₂=0; S₂³0.

2. Правую часть равенства всегда можно сделать неотрицательной, умножая обе части –1.

Например, равенство 2х₁ +3х₂ –7х₃= -5 эквивалентно равенству

- 2х₁ -3х₂ + 7х₃= 5

3. Знак неравенства изменяется на противоположный при умножении обеих частей на –1.

Переменные

Любую переменную х_i, не имеющую ограничения в знаке, можно представить как разность двух неотрицательных переменных:

x_i = x_i¢ - x_i¢¢, где x_i¢, x_i¢¢ ³ 0.

Такую подстановку следует использовать во всех ограничениях, которые содержат исходную переменную х_i, а также и в выражении для целевой функции.

Обычно находят решение задачи ЛП, в котором фигурируют переменные x_i¢ и x_i¢¢, а затем с помощью обратной подстановки определяют величину х_i. Важная особенность переменных x_i¢ и x_i¢¢ состоит в том, что при любом допустимом решении только одна из этих переменных может принимать положительное значение, т.е. если x_i¢>0, то x_i¢¢=0 и наоборот. Это позволяет рассматривать x_i¢ как остаточную переменную, а x_i¢¢ - как избыточную переменную, причем лишь одна из этих переменных может принимать положительное значение.

Целевая функция

Целевая функция линейной оптимизационной модели, представленной в стандартной форме, может подлежать как максимизации, так и минимизации. В некоторых случаях оказывается полезным изменить исходную целевую функцию.

Максимизация некоторой целевой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот.

Например, максимизация функции z = 5x₁ + 2x₂ + 3x₃ эквивалента минимизации функции (-z) = -5x₁ - 2x₂ - 3x₃

Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения переменных x₁, x₂ и x₃ в обоих случаях будут одинаковы. Отличие заключается только в том, что при одинаковых числовых значениях целевых функций их знаки будут противоположны.

Лекция 6:

СИМПЛЕКС - МЕТОД. ПРЕДСТАВЛЕНИЕ ПРОСТРАНСТВА РЕШЕНИЙ СТАНДАРТНОЙ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАМИРОВАНИЯ

Симплекс – метод (СМ) не обладает той наглядность, которая характерна для геометрического представления пространства решений. В его вычислительной схеме реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

Общую идею СМ можно проиллюстрировать на примере модели, построенной для задачи (краски). Пространство решений этой задачи представлено на рис.1. Исходной точкой алгоритма является начало координат (точка А на рис.1)

х_i Рис.1

E (4) D

(1)

(3) C

F (2)

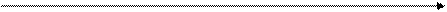A B x_e

Максимизировать Z= 3x_е + 2 x_i

при ограничениях x_е + 2 x_i £ 6 (1),

2x_е + x_i £ 8 (2),

-x_е + x_i £ 1 (3),

x_i £ 2 (4),

x_i ³ 0, x_е ³ 0

Решение, соответствующее этой точке, обычно называют начальным решением. От исходной точки осуществляется переход к некоторой смежной угловой точке. В рассматриваемом случае это может быть либо точка В, либо точка F. Выбор точки зависит от коэффициентов целевой функции. Так как коэффициент целевой функции при x_e больше коэффициента при x_i, а целевая функция подлежит максимизации, требуемое направление перехода соответствует увеличению x_e, что приводит к экстремальной точке В. После этого указанный процесс повторяется, чтобы выяснить, существует ли другая экстремальная точка, соответствующая лучшему допустимому решению (в данном случае большему значению целевой функции). Используя, как и ранее, информацию о целевой функции, можно определить, имеется ли на данном шаге алгоритма такая точка. В результате такой итеративный процесс позволяет найти оптимальную угловую точку С.

Выбор каждой последующей экстремальной точки при использовании СМ определяется следующими двумя правилами.

1. Каждая последующая угловая точка должна быть смежной с предыдущей. Например, в пространстве решений, изображенном на рис.1, невозможен прямой переход от точки А к точке С. Этот переход осуществляется по границам (ребрам) пространства решений: от точки А к точке В и лишь затем от точки В к точки С.

2. Обратный переход к предшествующей экстремальной точке не может производиться. Так, при движении в пространстве решений, представленном на рис.1, не должно быть обратного перехода от точки В к точке А.

Подводя итог изложению идей симплекс – метода, еще раз обратим внимание на то, что отыскание оптимального решения начинается с некоторой допустимой угловой точки, и все переходы осуществляются только к смежным точкам, причем перед новым переходом каждая из полученных точек проверяется на оптимальность. При решении задачи о красках начальным решением является точка А, из которой осуществляется переход в точку В и затем в точку С, соответствующую оптимуму. Таким образом, в данном случае для нахождения оптимального решения требуются три итерации (получаемые решения изображаются точками А.В и С).

Чтобы описать рассмотренные процедуры формальными средствами, необходимо определить пространство решений и угловые точки алгебраически. Требуемые соотношения устанавливают из указанного в таблице соответствия геометрических и алгебраических определений.

Геометрическое определение (графический метод)	Алгебраическое определение (симплекс – метод)
Пространство решений	Ограничения модели стандартной формы (рис.1)
Угловые точки	Базисные решения задачи в стандартной форме

Представление пространства решений с помощью алгебраических методов рассмотрим на примере о красках. Соответствующая линейная модель, приведенная к стандартной форме, имеет следующий вид:

Maксимизировать Z= 3x_е + 2 x_i +0S₁ +0S₂ +0S₃ +0S₄

при ограничениях x_е + 2 x_i + S₁ = 6

2x_е + x_i +S₂ = 8

-x_е + x_i +S₃ = 1

x_i +S₄ = 2

x_i ³ 0, x_е ³ 0, S₁, S₂, S₃, S₄ ³ 0

На рис. 2 представлено пространство решений данной задачи. Каждую точку этого пространства можно определить с помощью переменных x_e, x_i, S₁, S₂, S₃, S₄, фигурирующих в модели стандартной формы. Для идентификации нужной точки пространства решений воспользуемся тем, что при S_i=0, i=1,2,3,4, ограничения модели эквиваленты равенствам, которые представляются соответствующими ребрами пространства решений. Например, при S₁=0 первое ограничение задачи принимает вид равенства x_е + 2 x_i = 6, которое представляется ребром CD. Увеличение переменных S_i (S_i>0) будет соответствовать смещению допустимых точек с границ пространства решений в его внутреннюю область.

х_i Рис.2

G

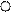
E S₄=0 D K

S₁=0

S₃=0 C

F S₂=0

x_e=0

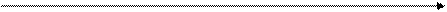ABx_e

x_i=0

Mинимизировать Z= 3x_е + 2 x_i

при ограничениях x_е + 2 x_i + S₁ = 6

2x_е + x_i +S₂ = 8

-x_е + x_i +S₃ = 1

x_i +S₄ = 2

x_i ³ 0, x_е ³ 0, S₁, S₂, S₃, S₄ ³ 0

Нас интересует прежде всего алгебраическое представление экстремальных точек. Анализируя рис.2, можно заметить, что переменные x_e, x_i, S₁, S₂, S₃, S₄, ассоциированные с экстремальными точками А, В, С, D, E,F можно упорядочить, исходя из того, какое значение (нулевое или ненулевое) имеет данная переменная в экстремальной точке.

Анализируя таблицу, легко заметить две закономерности:

1. Стандартная модель содержит четыре уравнения и шесть неизвестных, поэтому в каждой из экстремальных точек две (=6-4) переменные должны иметь нулевые значения.

2. Смежные экстремальные точки отличаются только одной переменной в каждой группе (нулевых и ненулевых переменных).

Экстремальная точка	Нулевые переменные	Ненулевые переменные
A	xe, xi	S1,S2,S3,S4
B	S2, xi	S1,xe,S3,S4
C	S2, S1	xi,xe,S3,S4
D	S4, S1	xi,xe,S3,S2
E	S4, S3	xi,xe,S1,S2
F	S3, xe	xi,S4,S1,S2

Первая закономерность свидетельствует о возможности определения экстремальных точек алгебраическим способом путем приравнивания нулю такого количества переменных, которое равно разности между количеством неизвестных и числом уравнений. В этом состоит сущность свойства однозначности экстремальных точек. На рис.2 каждой не экстремальной точке соответствует не более одной нулевой переменной. Так, любая точка внутренней области пространства решений вообще не имеет ни одной нулевой переменной, а любая не эктремальная точка, лежащая на границе, всегда имеет лишь одну нулевую переменную.

Свойство однозначности экстремальных точек позволяет определить их алгебраическим методом. Будем считать, что линейная модель стандартной формы содержит m уравнений и n (m £ n) не все допустимые экстремальные точки определяются как все однозначные неотрицательные решения системы m уравнений, в которых n – m переменных равны нулю.

Однозначные решения такой системы уравнений, получаемые путем приравнивания к нулю (n – m) переменных, называются базисными решениями. Если базисное решение удовлетворяет требованию неотрицательности правых частей, оно называется допустимым базисным решением. Переменные, имеющие нулевое значение, называются небазисными переменными, остальные – базисными переменными.

Из вышеизложенного следует, что при реализации СМ алгебраическое определение базисных решений соответствует идентификации экстремальных точек, осуществляемой при геометрическом представлении пространства решений. Таким образом, максимальное число итераций при использовании СМ равно максимальному числу базисных решений задачи ЛП, представленной в стандартной форме. Это означает, что количество итерационных процедур СМ не превышает

Cⁿ_m=n!/ [(n-m)!m!].

Вторая из ранее отмеченных закономерностей оказывается весьма полезной для построения вычислительных процедур СМ, при реализации которого осуществляется последовательный переход от одной экстремальной точки к другой, смежной с ней. Так как смежные экстремальные точки отличаются только одной переменной, можно определить каждую последующую (смежную) экстремальную точку путем замены одной из текущих небазисных (нулевых) переменных текущей базисной переменной. Таким образом, между множеством небазисных и множеством базисных переменных происходит взаимообмен переменными x_e и S₂. Этот процесс можно наглядно представить в виде следующей таблицы.

Экстремальная точка	Небазисные (нулевые) переменные	Базисные переменные
A	xe, xi	S1,S2,S3,S4
B	S2, xi	S1,xe,S3,S4

Применяя аналогичную процедуру ко всем экстремальным точкам рис.2, можно убедиться в том, что любую последующую экстремальную точку всегда можно определить путем взаимной замены по одной переменной в составе базисных и небазисных переменных (предыдущей смежной точки). Этот фактор существенно упрощает реализацию вычислительных процедур СМ.

Рассмотренный процесс взаимной замены переменных приводит к необходимости введения двух новых терминов. Включаемой переменной называется небазисная в данный момент переменная, которая будет включена в множество базисных переменных на следующей итерации (при переходе к смежной экстремальной точке). Исключаемая переменная – это та базисная переменная, которая на следующей итерации подлежит исключению из множества базисных переменных.

Лекция 7:

ВЫЧИСЛИТЕЛЬНЫЕ ПРОЦЕДУРЫ СИМПЛЕКС – МЕТОДА

Симплекс – алгоритм состоит из следующих шагов.

Шаг 0 Используя линейную модель стандартной формы, определяют начальные допустимые базисные решения путем приравнивания к нулю n-m (небазисных) переменных.

Шаг 1 Из числа текущих небазисных (равных нулю) переменных выбирается включаемая в новый базис переменная, увеличение которой обеспечивает улучшение значения целевой функции. Если такой переменной нет, вычисления прекращаются, т.к. текущее базисное решение оптимально. В противном случае осуществляется переход к шагу 2.

Шаг 2 Из числа переменных текущего базиса выбирается исключаемая переменная, которая должна принять нулевое значение (стать небазисной) при введении в состав базисной новой переменной.

Шаг 3 Находится новое базисное решение, соответствующее новым составам небазисных и базисных переменных. Осуществляется переход к шагу 1.

Поясним процедуры СМ на примере решения нашей задачи. Сначало необходимо представить целевую функцию и ограничения модели в стандартной форме:

Z - 3x_е + 2 x_i =0 (целевая функция)

при ограничениях x_е + 2 x_i + S₁ = 6

2x_е + x_i +S₂ = 8

-x_е + x_i +S₃ = 1

x_i +S₄ = 2

x_i ³ 0, x_е ³ 0, S₁, S₂, S₃, S₄ ³ 0

Как отмечалось ранее, в качестве начального пробного решения используется решение системы уравнений, в которой две (6-4=2) переменные принимаются равными нулю. Это обеспечивает единственность и допустимость получаемого решения. В рассматриваемом случае очевидно, что подстановка x_e=x_i=0 сразу же приводит к следующему результату: S₁ =6, S₂ =8, S₃ =1, S₄ =2. Полученные результаты удобно представить в виде таблицы:

Базисные переменные	z	xe	xi	S1	S2	S3	S4	Решение
z		-3	-2					0 z - уравнение
S1								6 S1 - уравнение
S2								8 S2 - уравнение
S3		-1						1 S3 - уравнение
S4								2 S4 - уравнение

Эта таблица интерпретируется следующим образом. Столбец «Базисные переменные» содержит переменные пробного базиса S₁, S₂, S₃, S₄ значения которых приведены в столбце «Решение». При этом подразумевается, что небазисные переменные x_i и x_е (не представленные в первом столбце) равны нулю. Значение целевой функции z= 3х0+2х0+0х6+0х8+0х1+0х2 равно нулю, что и показано в последнем столбце таблицы.

Как определить, является ли полученное пробное решение наилучшим (оптимальным)? Анализируя z – уравнение, нетрудно заметить, что обе небазисные переменные x_i и x_е , равные нулю, имеют отрицательные коэффициенты. Это эквивалентно наличию положительных коэффициентов при этих переменных в исходной целевой функции. Так как мы имеем дело с задачей максимизации, значение z может быть улучшено при увеличении как x_е, так и x_i. Однако всегда выбирается переменная с большим абсолютным значением отрицательного коэффициента (в z – уравнении), т.к. практический опыт вычислений показывает, что в этом случае оптимум достигается быстрее.

Это правило составляет основу используемого в вычислительной схеме СМ условия оптимальности, которое состоит в том, что, если в задаче максимизации все небазисные переменные в z – уравнении имеют неотрицательные коэффициенты, полученное пробное решение является оптимальным. В противном случае в качестве новой базисной переменной следует выбрать ту, которая имеет наибольший по абсолютной величине отрицательный коэффициент.

Применяя условие оптимальности к исходной таблице, выберем в качестве переменной, включаемой в базис, переменную x_е. Исключаемая переменная должна быть выбрана из совокупности базисных переменных S₁, S₂, S₃, S₄. Процедура выбора исключаемой переменной предполагает проверку условия допустимости, требующего, чтобы в качестве исключаемой переменной выбиралась та из переменных текущего базиса, которая первой обращается в нуль при увеличении включаемой переменной x_е вплоть до значения, соответствующего смежной экстремальной точке. В рамках алгебраического представления каждая из таких точек пересечения определяется отношением постоянной правой части ограничения к соответствующему положительному коэффициенту при включаемой переменной. Интересующее нас отношение (фиксирующее искомую точку пересечения и идентифицирующее исключаемую переменную) можно определить непосредственно из симплекс – таблицы (С-Т).

Для этого в столбце, соответствующем вводимой переменной x_е, вычеркиваются отрицательные и нулевые элементы ограничений. Затем вычисляются отношения постоянных, фигурирующих в правых частях этих ограничений, к оставшимся элементам столбца, соответствующего вводимой переменной x_е . Исключаемой переменной будет та переменная текущего базиса, для которой указанное выше отношение минимально. Начальная С-Т для нашей задачи, получаемая после проверки условия допустимости (т.е. после вычисления соответствующих отношений и определения исключаемой переменной), воспроизводится ниже.

Дата добавления: 2015-06-04