Стандартная форма линейных оптимизационных моделей 4 страница

Упражнение: Предположим, что в задаче фирмы Reddy Mikks целевая функция Z = 3х_Е + 2х₁ заменена на Z = 2х_Е + 5х₁; а ограничения модели не изменились. Решение задачи с помощью СМ приводит к следующему Z – уравнению:

Z + 2S₁ + S₄ = 14.

Оптимальные значения переменных равны Х_Е = Х₁ = 2, S₂ = 2 S₃ = 1. Все остальные переменные имеют нулевое значение.

1. Определите статус каждого из 4 ресурсов, фигурирующих в модели.

Ответ: Ресурсы 1 и 4 дефицитные, ресурсы 2 и 3 недефицитные.

2. Определите теневую цену каждого из 4-х ресурсов.

Ответ: у₁ = 2; у₂ = у₃ = 0; у₄ = 1.

3. Можно ли улучшить оптимальное значение Z, увеличив запас продукта В?

Ответ: Нет, поскольку у₂ = 2, то есть данный ресурс является недефицитный.

4. Так как у₄ = 1, то, увеличение 4-го ресурса, можно добиться улучшения оптимального значения Z. Дайте экономическую интерпретацию увеличению объема «использования» четвертого ресурса.

Ответ: Четвертое ограничение фиксирует предельный уровень спроса. Увеличение объема «использования» 4-го ресурса эквивалентна увеличению сферы влияния фирмы на рынке сбыта.

5. Какому из ресурсов следует отдать предпочтение при вложении дополнительных средств?

Ответ: Вложения следует направить прежде всего на увеличение запасов продукта А, так как ему соответствует наибольшая теневая цена у₁ = 2.

Максимальное изменение запаса ресурса

При решении вопроса о том, запас какого из ресурсов следует увеличивать в первую очередь, обычно используются теневые цены. Чтобы определить интервал значений изменения запаса ресурса, при которых теневая цена данного ресурса, фигурирующая в заключительной симплекс-таблице, остается неизменной, необходимо выполнить ряд дополнительных вычислений. Рассмотрим сначала соответствующие вычислительные процедуры, а затем покажем, как требуемая информация может быть получена из симплекс-таблицы для оптимального решения.

Положим, что в задаче фирмы Reddy Mikks запас первого ре­сурса изменился на D₁ т. е. запас продукта А составит 6+D₁ тонн. При положительной величине D₁ запас данного ресурса увеличи­вается, при отрицательной - уменьшается. Как правило, иссле­дуется ситуация, когда объем ресурса увеличивается (D₁>0). Однако, чтобы получить результат в общем виде, рассмотрим оба случая.

Как изменится симплекс-таблица при изменении величины за­паса ресурса на D₁? Проще всего получить ответ на этот вопрос, если ввести D₁ в правую часть первого ограничения начальной сим­плекс-таблицы и затем выполнить все алгебраические преобразова­ния, соответствующие последовательности итераций. Поскольку правые части ограничений никогда не используются в качестве ведущих элементов, то очевидно, что на каждой итерацииD₁ будет оказывать влияние только на правые части ограничений. Читателю предлагается самостоятельно проверить, что результаты, получае­мые на соответствующих итерациях при решении рассматриваемой задачи, идентичны данным, приведенным в табл. 3.7.

Таблица 3.7

Уравнение	Значения элементов правой части на соответствующих итерациях
(начало вычислений)		(оптимум)
Z
	6 + D1	2 + D1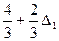
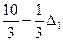
			3-1D1

Фактически все изменения правых частей ограничений, обуслов­ленные введением D₁, можно определить непосредственно по данным, содержащимся в симплекс-таблицах. Прежде всего заметим, что на каждой итерации новая правая часть каждого ограничения пред­ставляет собой сумму двух величин: 1) постоянной и 2) члена, ли­нейно зависящего от D₁. Постоянные соответствуют числам, которые фигурируют на соответствующих итерациях в правых частях ограничений симплекс-таблиц до введения D₁. Коэффициенты при D₁ во вторых слагаемых равны коэффициентам при s₁ на той же ите­рации. Так, например, на последней итерации (оптимальное реше­ние) постоянные (12* 2/3, 4/3, 10/3, 3, 2/3) представляют собой числа, фигурирующие в правых частях ограничений оптимальной симп­лекс-таблицы до введения D₁. Коэффициенты (1/3, 2/3, -1/3, -1, 2/3) равны коэффициентам при s₁ в той же симплекс-таблице пото­му, что эта переменная связана только с первым ограничением. Другими словами, при анализе влияния изменений в правых частях второго, третьего и четвертого ограничений нужно пользоваться коэффициентами при переменных s₂, s₃ и s₄ соответственно.

Какие выводы можно сделать из полученных результатов? Так как введение D₁ сказывается лишь на правой части симплекс-таблицы, изменение запаса ресурса может повлиять только на допустимость решения. Поэтому D₁ не может принимать значений, при которых какая-либо из (базисных) переменных становится отри­цательной. Из этого следует, что величина D₁ должна быть огра­ничена таким интервалом значений, при которых выполняется ус­ловие неотрицательности правых частей ограничений в результи­рующей симплекс-таблице, т. е.

X₁ = 4/3 + (2/3)D₁ ³ 0, (1)

X_E = 4/3 + (1/3) D₁ ³ 0, (2)

S₃ = 3 - D₁ ³ 0, (3)

S₄ = 2/3 – (2/3) D₁ ³ 0. (4)

Для определения допустимого интервала изменения D₁ рассмо­трим два случая.

Случай 1: D₁ > 0. Соотношение (1) всегда выполняется при D₁ > 0. Соотношения (2), (3) и (4) определяют следующие предельные зна­чения D₁: D₁ £ 10, D₁ £ 3 и D₁ £ 1. Таким образом, все четыре соот­ношения выполняются при D₁ £ 1.

Случай 2: D₁ < о. Соотношения (2), (3) и (4) всегда выполняются при D₁ <о, тогда как соотношение (1) справедливо только при D₁ ³ -2.

Объединяя результаты, полученные для обоих случаев, можно сделать вывод, что при –2 £ D₁ £ 1 решение рассматриваемой зада­чи всегда будет допустимым. Любое значение D₁, выходящее за пределы указанного интервала (т. е. уменьшение запаса продукта А более чем на 2 т или увеличение более чем на 1 т), приведет к недопу­стимости решения и новой совокупности базисных переменных (см. гл. 4).

Упражнение 3.4.3. Рассмотрите задачу фирмы Reddy Mikks.

(а) Найдите новое оптимальное решение задачи, если D₁ ==1/2 т. [Ответ: z = 12·5/6, x_E = 3 1/6, x₁ = 2/3, s₁ = s₂ = 0, s₃ = 2 ½, s₄ = 1/3.]

(б) Определите правые части ограничений заключительной симплекс-таблицы

- при изменении запасов ресурсов 2, 3 и 4 на D₂, D₃ и D₄ соответственно.

[Ответ: D₂: 4/3 - D₂/3, 10/3 +2D₂/3, 3 + D₂, 2/3 + D₂/3;

D₃: 4/3, 10/3, 3+D₃, 2/3;

D₄: 4/3, 10/3, 3, 2/3 + D₄.]

(в) Применительно к п. (б) определите допустимыеинтервалы изменения D₂, D₃ и D₄.

[Ответ: D₂: -2 £ D₂ £ 4, -3 £ D₃ < ¥, -2/3 £ D₄ < ¥,]

(г) Определите интервалы изменения оптимальных значений z, соответствующие результатам, полученным в п. (в).

[Ответ: D₂: 10 £ z £ 18. D₃ и D₄: z = 12·2/3 независимо от значений Dз иD₄. Эти результаты согласуются с результатами выполненного ранее анализа ценности ресурсов.]

(д) Будут ли справедливы результаты, полученные в п. (г), если D₂, D₃ и D₄ вво­дятся одновременно?

[Ответ. Нет, поскольку при одновременном изменении запасов ресурсов2, 3 и 4 элементы правых частей ограничений симплекс-таблицы становятся функциями D₂, Dз и D₄. Полученные ранее результаты справедливы лишь тогда, когда рассматривается изменение запаса только одного из ресурсов.]

Максимальное изменение коэффициентов удельной

прибыли (стоимости)

Наряду с определением допустимых изменений запасов ресур­сов представляет интерес и установление интервала допустимых изменений коэффициентов удельной прибыли (или стоимости). В подразд. 2.1.2 (третья задача анализа на чувствительность) на основе графического представления модели было показано, что при определенных значениях изменения коэффициентов целевой функции оптимальные значения переменных остаются неизменными (хотя оптимальное значение z при этом меняется). Возвращаясь к этому вопросу, покажем, каким образом интересующую нас ин­формацию можно получить из данных, содержащихся в заключи­тельной симплекс-таблице.

Следует отметить, что уравнение целевой функции также ни­когда не используется в качестве ведущего уравнения. Поэтому лю­бые изменения коэффициентов целевой функции окажут влияние только на z-уравнение результирующей симплекс-таблицы. Это означает, что такие изменения могут сделать полученное решение неоптимальным. Наша цель заключается в том, чтобы найти интер­валы значений изменений коэффициентов целевой функции (рас­сматривая каждый из коэффициентов отдельно), при которых оп­тимальные значения переменных остаются неизменными.

Чтобы показать, как выполняются соответствующие вычисле­ния, положим, что удельная прибыль от производственной деятель­ности, ассоциированной с переменной x_E (задача фирмы Reddy Mikks) изменяется от 3 до 3+ d₁, где d₁ может быть как положитель­ным, так и отрицательным числом. Целевая функция в этом случае принимает следующий вид:

Z = (3 + d₁) x_E + 2x₁.

Если воспользоваться данными начальной симплекс-таблицы и выполнить все вычисления, необходимые для получения заключи­тельной симплекс-таблицы, то последнее z-уравнение будет выгля­деть следующим образом:

Базисные переменные	xE x1 s1 s2 s3 s4	Решение
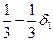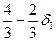z	0 0 0 0

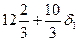
Коэффициенты при базисных переменных x_E, x₁ и остаточных переменных s₃, s₄ остаются равными нулю. Это уравнение отличается от z-уравнения до введения d₁ только наличием членов, содержащих d₁. Коэффициенты при d₁ равны коэффициентам при соответствующих переменных в x_E-уравнении симплекс-таблицы для полученного ра­нее оптимального решения

Базисные переменные	xE x1 s1 s2 s3 s4	Решение
xE	1 0 -1/3 2/3 0 0	10/3

Мы рассматриваем x_E-уравнение, так как коэффициент именно при этой переменной в выражении для целевой функции изменился на d₁.

Оптимальные значения переменных будут оставаться неизмен­ными при значениях d₁, удовлетворяющих условию неотрицатель­ности (задача на отыскание максимума) всех коэффициентов при не­базисных переменных в z- уравнении. Таким образом, должны вы­полняться следующие неравенства:

1/3 - d₁/3 ³ 0, (1)

4/3 +2d₁/3 ³ 0. (2)

Из первого неравенства получаем, что d₁ £ 1, а из второго следует, что d1 ³ -2. Эти результаты определяют пределы изменения ко­эффициента c₁ в виде следующего соотношения: -2 £ d₁ £ 1. Та­ким образом, при уменьшении коэффициента целевой функции при переменной хе до значения, равного 3+ (—2)==1, или при его уве­личении до 3+1 ==4 оптимальные значения переменных остаются неизменными (сравните с результатом, полученным при рассмотре­нии третьей задачи анализа на чувствительность, подразд. 2.1.2). Однако оптимальное значение z будет изменяться (в соответствии с выражением где –2 £ d₁ £ 1).

Упражнение 3.4.4. Пусть в задаче фирмы Reddy Mikks коэффициент це­левой функции при переменной x₁ изменился на величину d₂. Определите интер­вал значений бд, при которых оптимальные значения переменных остаются неизменными.

[Ответ: -1/2 £ d₂ £ 4, z = 12 2/3 + 4/3 d₂.]

Все предыдущее обсуждение касалось исследования изменений коэффициента при переменной, которой поставлено в соответствие ограничение, фигурирующее в симплекс-таблице. Однако такое ограничение имеется лишь в том случае, когда данная переменная является базисной (например, x_E и x₁). Если переменная небазис­ная, то в столбце, содержащем базисные переменные, она не будет представлена.

Любое изменение коэффициента целевой функции при небазисной переменной приводит лишь к тому, что в заключительной симплекс-таблице изменяется только этот коэффициент. Рассмотрим в ка­честве иллюстрации случай, когда коэффициент при переменной s₁ (первой остаточной переменной) изменяется от 0 до d₃. Выполне­ние преобразований, необходимых для получения заключительной симплекс-таблицы, приводит к следующему результирующему z-уравнению:

Базисные переменные	xE x1 s1 s2 s3 s4	Решение
z	1 0 1/3-d3 4/3 0 0	12 2/3

Из приведенного фрагмента заключительной симплекс-таблицы вид­но, что единственное отличие от z-уравнения до введения 6з состо­ит в том, что коэффициент при s₁ уменьшился на d₃. Таким образом, коэффициент при небазисной переменной в результирующем z- уравнении нужно уменьшить на ту же величину, на которую он увеличивается в исходном z-уравнении.

Задачи: Тема: СМ и вычислительные процедуры С –Т.

№3.3. Задано трехмерное пространство решений задачи ЛП с экстремальными точками А, В, С,…J. Координаты этих точек указаны на рис.

Х₃

A: (0;0;0)

D G В: (1;0;0)

С: (0;1;0)

F J H D: (0;0;1)

B X₁

A I

C E

X₂ рис. 1.

а) Являются ли следующие пары экстремальных точек смежными? (А;В) (В;D) (E;H) (A;I)

б) Пусть процесс решения задачи с помощью СМ начинается с т. А и заканчивается нахождением оптимума в т. H путём реализации следующих переходов от одной экстремальной точки к другой?

1). А ® B ® G ® H 4). A ® I ® H

2). A ® F ® J ® H 5). A ® D ® G ® H

3). A ® C ® I ® H 6). A ® D ® A ® B ® G ® H

7). A ® C ® F ® D ® A ® B ® G ® H

№3.4. На рис.1 все ограничения, определяющие пространство решений, имеют знак £. Пусть S₁; S₂; S₃ и S₄ – остаточные переменные, ассоциированные с ограничениями, которые представляются плоскостями CEIJF, BEIHG, DFJHG и HIJ соответственно. Идентифицируйте базисные и небазисные переменные, соответствующие каждой допустимой экстремальной точке. (Указание: подразумевается, что Х₁; Х₂; Х₃ ³ 0)

№3.5. Для условий задачи 3.4. определите включаемые в базис и исключаемые из базиса переменные для итераций, соответствующие переходам между следующими парами экстремальных точек:

A ® B; E ® I; F ® J; D ® G.

№3.6. Рассмотрим следующую задачу:

максимизировать: Z = 2х₁ – 4х₂ + 5х₃ + 8х₄

при ограничениях: х₁ + 4х₂ – 2х₃ + 8х₄ £ 2

-х₁ + 2х₂ +3х₃ + 4х₄ £ 1

х₁; х₂; х₃; х₄ ³ 0.

а). Определите мах количество возможных базисных решений?

б). Идентифицируйте допустимые экстремальные точки.

в). Найдите д. Б. Р.

№3.7. Пусть при решение задачи, условия которой соответствуют рис.1., исходной точкой (начальным решением) является точка А. Определите переменную, вводимую в базис на первой итерации, значение этой новой базисной переменной и улучшение значения максимальной целевой функции, если она имеет следующий вид:

а). Z = х₁ – 2х₂ + 3х₃

б). Z = 5х₁ + 2х₂ +4х₃

в). Z = -2х₁ + 7х₂ + 2х₃

г). Z = х₁ + х₂ +х₃

№ 3.8. Пусть для условий, соответствует рис. 2 задана следующая целевая функция:

максимизировать: Z = 3х₁ + 6х₂

Х₂ рис.2 Х₂

4 4

3 3

2 F 2 F E D

1 G G 1 C

0 A Х₁ А B Х₁

-1 -1 1 2 3 4 5 -1 -1 1 2 3 4 5

а). Найдите графическим способом оптимальную экстремальную точку.

б). Пологая, что реализация СМ начинается с т. А, определите последовательность экстремальных точек, приводящую к оптимуму, найденному в п.(а).

в). Пологая, что реализация СМ начинается с т. А, определите вводимую в базис переменную и отношения, используемые при проверке условия допустимости, если целевая функция имеет вид:

максимизировать: Z = 4х₁ + х₂

д). Применительно к условиям пп. (в) и (г) определите результирующее улучшение целевой функции.

№ 3.9. Дана следующая система уравнений:

х₁ + 2х₂ – 3х₃ + 5х₄ + х₅ = 4

5х₁ – 2х₂ + 6х₄ + х₆ = 8

2х₁ + 3х₂ – 2х₃ + 3х₄ + х₇ = 3

-х₁ + х₃ + 2х₄ + х₈ = 0

х₁; х₂ … х₈ ³ 0.

Известно начальное базисное решение (х₅ … х₈) базис вводится переменная х₁. Какая из переменных предыдущего базиса должна стать нулевой небазисной переменной, чтобы все переменные остались неотрицательными, и каково значение х₁ в новом базисном решении? Дайте ответ на поставленные вопросы для случаев, когда в базис вводятся переменные х₂; х₃; х₄.

№3.10. В нижесл. таблице приведены результаты некоторой итерации СМ.

Базисные переменные	х1 х2 х3 х4 х5 х6 х7 х8	Решение
Z	0 -5 0 4 -1 -10 0 0
Х8 Х3 Х1	0 3 0 -2 -3 -1 5 1 0 2 1 3 1 0 3 0 1 -1 0 0 6 -4 0 0

а). Определите исключаемую из базиса переменную, если в базис вводятся переменные: 1) х₂; 2) х₄; 3) х₅; 4) х₆; 5) х₇.

б). Для каждого из случаев, перечисленных в пункте (а), определите результирующее увеличение или уменьшение целевой функции Z.

№ 3.11. Решите следующие системы линейных уравнений, используя процедуру преобразования спрос (Гаусса – Жордана), являющуюся составной частью СМ.

а). –3х₁ + 2х₂ + 5х₃ = 5

4х₁ + 3х₂ + 2х₃ = 8

х₁ – х₂ + 3х₃ = 10

б). х₂ + х₃ = 5 (на экзамен)

2х₁ + х₂ – х₃ = 12

х₁ + 3х₂ + 4х₃ = 10

№ 3.12. Дана следующая совокупность ограничений:

х₁ + 7х₂ + 3х₃ + 7х₄ £ 46

3х₁ – х₂ + х₃ + 2х₄ £ 8

2х₁ + 3х₂ – х₃ + х₄ £ 10

Решите задачу ЛП СМ при следующих целевых функциях:

а). максимизировать Z = 2х₁ + х₂ – 3х₃ + 5х₄

б). максимизировать Z = -2х₁ + 6х₂ + 3х₃ – 2х₄

в). максимизировать Z = 3х₁ – х₂ + 3х₃ +4х₄

г). минимизировать Z = 5х₁ – 4х₂ + 6х₃ + 8х₄ ý (на экзамен).

д). минимизировать Z = 3х₁ – 6х₂ – 2х₃ + 4х₄

№ 3.13. Решите следующую задачу, анализируя и обосновывая ход решения, исходя из положений, на которых базируется СМ.

максимизировать Z = 5х₁ – 6х₂ + 3х₃ – 5х₄ + 12х₅

при ограничениях х₁ + 3х₂ + 5х₃ + 6х₄ + 3х₅ £ 90

х₁ … х₅ ³ 0

№ 3.14. Рассмотрим следующую задачу ЛП:

максимизировать Z = х₁ - 3х₂ – 2х₃

при ограничениях 3х₁ – х₂ + 2х₃ £ 7

-2х₁ + 4х₂ £ 12

-4х₁ + 3х₂ + 8х₃ £ 10

х_1; х₂; х₃ ³ 0.

а). Решите задачу СМ, выбирая на каждой итерации в качестве новой базисной переменной ту небазисную переменную, которая в Z – уравнение имеет наибольший положительный коэффициент.

б). Решите задачу СМ, выбирая в качестве новой базисной переменной ту небазисную переменную, которая имеет в Z – уравнение наименьший положительный коэффициент.

в). Сравните количество итераций, потребовавшихся для решения задачи в пп (а) и (б).

г). Если требование минимизации целевой функции заменяется требованием ее максимизации, исходную целевую функцию умножают на (-1), и при реализации СМ используют условие оптимальности, соответствующую процессу максимизации. Как изменяются при этом вычислительные процедуры СМ по сравнению со случаем, когда целевая функция должна была минимальна?

№3.15. Решите следующую задачу, используя для получения начального (допустимого) базисного решения переменные х₄; х₅; х₆.

минимизировать Z = 3х₁ + х₂ + 2х₃

при ограничениях 12х₁ + 3х₂ + 6х₃ + 3х₄ = 9

8х₁ + х₂ – х₄ + 2х₅ = 10

3х₁ –х₆ = 0 х₁, … х₆ ³ 0

Тема: Искусственные переменные и М – метод.

№3.16. Рассмотрите систему ограничений:

-2х₁ + 3х₂ = 3 (1)

Дата добавления: 2015-06-04