Теоретическая часть. Спектр псевдошумовых последовательностей и генерация шума

Спектр псевдошумовых последовательностей и генерация шума

Лабораторная работа №14.

Псевдошумовые последовательности (ПШ последовательности, псевдослучайные последовательности, PN последовательности) – тип сигналов, широко применяющийся в разных системах модуляции, таких как CDMA и DSSS. Также эти последовательности могут быть использованы в экспериментальных целях для моделирования шума.

Для того, чтобы понять что именно представляют собой ПШ последовательности, необходимо вернуться к рассмотрению спектра последовательностей импульсов. Вспомним, что все импульсы состоят из теоретически бесконечного набора синусоидальных колебаний – основного и производных гармоник, по частоте кратных основному. Частота и амплитуда гармоник зависит от частоты импульсов и их скважности. Но при всем этом, спектральные композиции всех импульсных последовательностей имеет вид функции кардинального синуса и выглядят примерно так, как показано на рисунке 14.1.

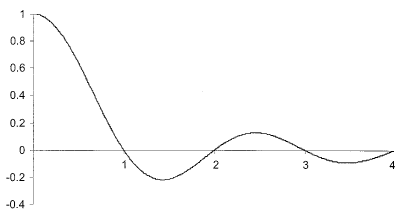
Рисунок 14.1

Рисунок 14.2 иллюстрирует пример для последовательности прямоугольных импульсов с частотой 1кГц и скважностью равной 50%.

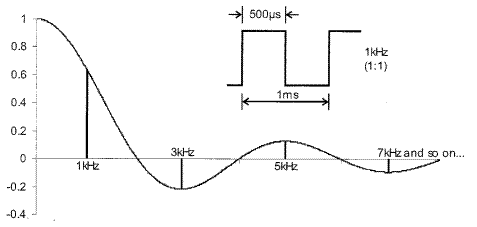
Рисунок 14.2

Рисунок 14.3 показывает спектральную композицию последовательности прямоугольных импульсов с частотой 1кГц и скважностью 25%. Заметьте, что график также имеет вид функции кардинального синуса.

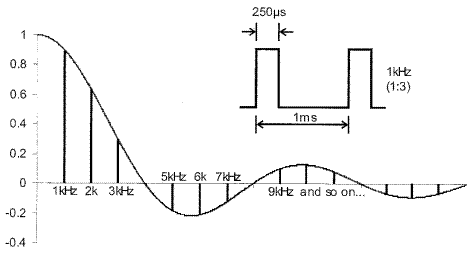
Рисунок 14.3

Примеры на рисунках 14.2 и 14.3 показательны. Во-первых, они показывают нам, что некоторые гармоники импульсных последовательностей имеют амплитуду равную нулю. Во-вторых, чем меньше скважность импульсов, тем больше значащих гармоник появляется в спектре сигнала.

Теперь предположим, что генератор последовательностей продолжительное время воспроизводит последовательность, состоящую из четырех бит 1000, каждый длительностью 250µs (т.е. тактовая частота равна 4кГц). Во временной области этот сигнал будет идентичен сигналу, представленному на рисунке 14.3. Это значит, что и его спектральная композиция будет идентична спектру сигнала на рисунке 14.3.

У этого факта есть несколько полезных следствий. Во-первых, мы выявили общее правило для определения нулевых гармоник в повторяющейся двоичной последовательности. Они имеют частоты, кратные тактовой частоте цифрового сигнала. В нашем случае, при четырехбитной последовательности 1000 и тактовой частоте 4кГц, нули появляются на частотах 4кГц, 8кГц, 12кГц и так далее.

Во-вторых, если генератором последовательности будет воспроизводится последовательность из пяти бит 10000, скважность сигнала уменьшится и ещё больше гармоник будут представлены между нулевыми. Важно, что при тактовой частоте 4кГц и пятибитной последовательности нули появляются на тех же частотах, что и на рисунке 3. Итак, если нули появляются на тех же частотах, но между ними будет присутствовать больше гармоник, то спектральная композиция пятибитной последовательности будет богаче, чем у четырехбитной. Отсюда можем сделать ещё один общий вывод. Чем больше количество бит в повторяющейся последовательности при заданной тактовой частоте, тем богаче спектральная композиция сигнала.

Используя функцию кардинального синуса для спектрального анализа последовательностей 1000, 10000, 100000 и т.д. покажет, что число гармоник в каждой доле функции равно числу бит в последовательности (с учетом того, что последняя гармоника равна нулю).

Итак, мы вновь возвращаемся к понятию псевдошумовых последовательностей. Если длина повторяющейся двоичной последовательности достаточно велика, ее спектральная композиция настолько плотная, что может быть использована для моделирования белого шума в определенном спектре частот. Из-за присутствия в этом шумовом сигнале повторяющегося элемента эти последовательности называют псевдо- или почти шумовыми.

Дата добавления: 2015-06-04