Показатели вариации, способ их вычисления

При изучении совокупности явления нельзя ограничиваться только нахождением средней величины.

Средние величины дают обобщенную характеристику варьирующего признака, показывают типичные характеристики для изучаемой совокупности. Однако в средней величине не проявляется степень колеблемости отдельных значений признаков (вариант) вокруг среднего уровня. В зависимости от однородности в совокупности колеблемость признаков может быть большой или, наоборот, малой. Поэтому возникает необходимость в измерении вариации отдельных вариантов по отношению к средней величине.

Для большей убедительности приведем два ряда набора чисел:

I ряд — 6, 10,14,26,34; II ряд— 14,16,18,20,22.

Определим среднюю арифметическую ():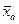

для I ряда ; для II ряда .

Таким образом, два совершенно различных ряда имеют одну и ту же среднюю (х_а = 18). Отсюда следует, что эти средние не характеризуют внутреннего содержания совокупности/

В результате простого обозрения видно, что в первом ряду ко­леблемость признаков больше, чем во втором.

Для измерения пестроты, колеблемости (вариации) изучаемого признака в данной совокупности статистики применяются различ­ные показатели.

Рассмотрим сначала размах вариации (R).

Размах колебаний (R) — это разность между наибольшей и наименьшей вариантной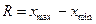

Для предыдущего примера амплитуда вариации составляет:

R₁(I ряда) = 34 - 6 = 28 единиц;R₁₁(II ряда) = 22 - 146 = 8 единиц.

Таким образом, можно сделать вывод, что первый ряд распределения имеет значительно большую амплитуду вариант, чем вто­рой ряд распределения.

Однако ограничиться определением вариации будет неверно, потому что этот показатель дает только общее, внешнее представ­ление о колеблемости, о пределах вариации, но не характеризует степени колебаний данного признака в этих пределах.

Размах вариации улавливает только крайние отклонения, но не отражает размера отклонений всех вариант. По показателям откло­нений оценивается надежность вычисленной средней величины, т. е. выявляется, можно ли пользоваться рассчитанной средней величи­ной.

Дата добавления: 2015-06-25