Дисперсия

Дисперсия — это средний квадрат отклонения всех значе­ний признака ряда распределения от средней арифметической.

Именно дисперсия и среднее квадратическое отклонение явля­ются основными наиболее употребляемыми показателями вариации.

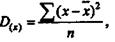
Обозначается дисперсия буквой

где х — значение признака;

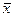- средняя арифметическая;

п — численность совокупности.

Но

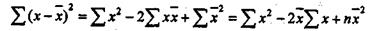
Поделив это выражение на п, учтем, что 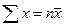. Тогда

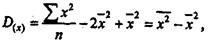
т. е. дисперсия равна разности среднего квадрата вариантов и квад­рата их средней (подразумевая здесь под "средней" среднюю ариф­метическую). И, наконец,

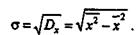
Заменяя в формуле определения дисперсии (D_x) среднее суммами, разделенными на численность совокупности, получим формулу:

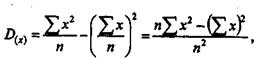
имеющую некоторые технические преимущества для ее вычисле­ния. При ее применении округление производится только один раз и в самом конце вычисления.

Пример. В табл. 15 приведены данные для расчета дисперсии и среднего квадратического отклонения на примере стажа продав­цов торговой фирмы "Элегант", работающих в двух ее магазинах.

Для 1-го магазина:

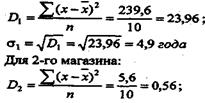Таблица.15

Данные для расчета дисперсии и среднего квадратического отклонения по стажу продавцов в двух магазинах фирмы "Элегант"

п/п	1-й магазин	2-й магазин
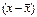
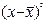
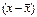
Стаж продавцов, лет (x)	отклонения от среднего	Квадрат отклонения	Стаж продавцов, лет (x)	отклонения от среднего	Квадрат отклонения
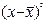
		-6,2	38,44		-1,2	1,44
		-5,2	27,04		-1,2	1,44
		-4,2	17,64		-0,2	0,04
		-4,2	17,64		-0,2	0,04
		-3,2	10,24		-0,2	0,04
б		1,8	3,24		-0,2	0,04
		2,8	7,84		0,8	0,64
		4,8	23,04		0,8	0,64
		2,8	33,64		0,8	0,64
		7,8	60,84		0,8	0,64
Итого			239,60			5,6

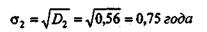
Таким образом, стаж продавцов отклоняется от среднего для первого магазина на 4,9 года, а для второго магазина — 0,75 года. Формула дисперсии для вариационного ряда с вариантами х и час­тотами/будет иметь вид:

где х — значение признака; 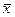— средняя арифметическая; f — частота.

Дата добавления: 2015-06-25