Показатели вариации. Понятие вариации, ее виды

Понятие вариации, ее виды

Вариация ¾ это различия в значениях признака и единиц совокупности.

Она складывается под влиянием различных внутренних и внешних причин, действующих в различных направлениях.

Задачи статистического изучения вариации:

· Изучение степени вариации признака;

· Определение роли различных факторов в формировании разброса значение признака.

Изучение вариации в статистике имеет важное значение. Измерение вариации необходимо при проведении выборочных наблюдений, изучении взаимосвязей, определении однородности совокупности и типичности средней.. Воздействие на эти причины позволит уменьшить вариацию.

Виды вариации:

1) вариация в пространстве – это различия в значениях признака у единиц совокупности, взятых в одно время;

2) вариация во времени – это различия в значениях признака у одной единицы совокупности в различные моменты времени.

Для измерения вариации в статистике применяют следующую систему показателей.

Абсолютные показатели:

1) размах вариации (R);

2) среднее линейное отклонение (l);

3) дисперсия (σ²);

4) среднее квадратическое отклонение – СКО (σ).

Относительные показатели:

1) коэффициент осцилляции (V_R);

2) коэффициент вариации (V_σ).

1. Размах вариации — это различие между крайними значениями признака

R = X_max-X_min

Недостатки:

1) не учитывает повторяемость значения признака;

2) если крайние значения являются аномальными, то размах не дает истинной картины вариации значений.

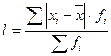2. Среднее линейное отклонение — среднее абсолютное отклонение значений признака от своей средней, используется при анализе ритмичности производства, равномерности поставок товаров, изучении состава работников и т. д.

3. Общепринятым показателем вариации является дисперсия.

Дисперсия — это средний квадрат отклонений индивидуальных значений от своей средней. Она не имеет единиц измерения.

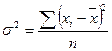Простая дисперсия (используется по не сгруппированным данным и при изучении вариации во времени);

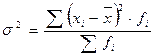Взвешенная дисперсия (используется по рядам распределения):

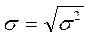4. Среднеквадратическое отклонение – это корень квадратный из дисперсии (СКО), оно характеризует средний разброс индивидуальных значений вокруг своей средней.

СКО имеет те же единицы измерения, что и признак.

5. Коэффициент осцилляции — он характеризует максимальную степень разброса индивидуальных значений вокруг средней.

V_R = R / x_ср. •100%

6. Коэффициент вариации — он характеризует среднюю степень разброса индивидуальных значений вокруг средней.

V_σ = σ / x_ср. •100%

Относительные показатели (V_R, V_σ) используются для сравнения вариаций по различным совокупностям или по одной совокупности за разное время. V_δ используется также для характеристики однородности совокупности по данному признаку.

V _σ < 33%- совокупность однородная,

V _σ ≥ 33%- совокупность неоднородная.

3. Свойства σ ² и σ, формулы их расчета.

Свойства:

1) Дисперсия и СКО σ ² и σ – постоянной величины = 0.

2) Если все значения признака (x_i) уменьшить или увеличить на число а, то дисперсия и СКО σ ² и σ не изменятся.

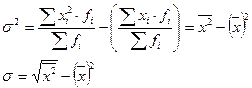3) Если все значения признака (x_i) умножить или разделить на число k, то σ ² изменится в k ² раз, а σ – в k раз.

– упрощенная формула расчета дисперсии и СКО.

Используя свойства дисперсии и СКО можно найти дисперсию признака в интервальных рядах распределения методом моментов:

1) находим середины интервалов x_i;

2) преобразуем данные x_i^׀ = (x_i – A) / k, где А – середина интервала с наибольшей частотой, k – ширина интервала;

3) определяем среднюю для преобразованных данных

x_ср^׀ = ∑ x_i^׀f_i / ∑ f_i;

4) определяем начальную дисперсию

σ ² = k ²• (∑(x_i ^׀)² f_i / ∑ f_i – (x_ср ^׀)²)

Для нормального закона распределения для показателей вариации существует взаимосвязь.

R ≈ 6 · σ

σ = 1,25· l

Правило трех сигм для нормального закона распределения – в интервал

(x – 3 σ, x + 3 σ)  попадает 99,7% всех индивидуальных значений x_i.

Коэффициент асимметрии можно найти по формуле

_

K_as = (x – M_o)/σ

K_as находится в интервале от -3 до 3. Чем ближе к 0, тем асимметрия слабее, чем ближе по модулю к 3, тем сильнее.

Дата добавления: 2015-06-25