Примеры решения задач по квантовой физике

Задача 1. Найти длину волны де Бройля для электрона, кинетическая энергия которого равна:
1) 10 кэВ, 2) 1 МэВ.

Дано: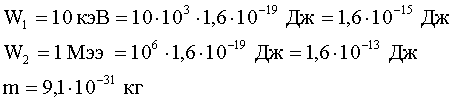
Найти:

Решение: Длина волны де Бройля связана с импульсом:

где 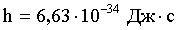- постоянная Планка;
р - импульс частицы.

Импульс частицы зависит от ее скорости. Если скорость движения частицы много меньше скорости света в вакууме (v<<c), то это случай нерелятивистский. Если скорость движения частицы соизмерима со скоростью света в вакууме, то это случай релятивистский. Импульс частицы связан с энергией. Поэтому, чтобы выяснить, какой это случай, вычислим энергию покоя частицы и сравним ее с энергией движущейся частицы. Вычислим энергию покоя электрона:

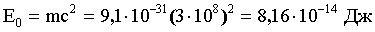
Сравним кинетическую энергию электрона с энергией покоя E₀. В первом случае W₁<<E₀, значит это случай нерелятивистский и импульс равен: p = mv. Импульс связан с кинетической энергией соотношением:

Отсюда:

Тогда:

Во втором случае , значит это случай релятивистский. Импульс равен: , где с - скорость света. Тогда:

Ответ: ,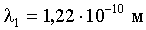

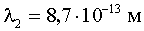
Задача 2. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности?

Дано: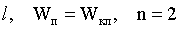
Найти:	x.

Решение: Волновая функция ψ, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме шириной l, имеет вид:

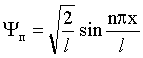(1)

где n - номер энергетического уровня (n = 1,2,3...),
х - координата частицы в яме (0 ≤ х ≤ l).

Согласно физическому смыслу волновой функции:

(2)

где w - плотность вероятности обнаружения частицы в точке с координатой х.

Если частица находится на втором энергетическом уровне (n = 2), т.е.:

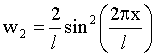(3)

Выражение для классической плотности вероятности имеет вид:

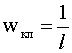(4)

Приравнивая по условию выражения (3) к (4), получим:

(5)

Решая уравнение (5), найдем:

В пределах ямы (0 ≤ х ≤ l) таких точек четыре:

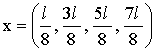
Ответ: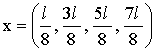

Задача 3. Некоторый примесный полупроводник имеет решетку типа алмаза и обладает только дырочной проводимостью. Определить концентрацию дырок n_р и их подвижность u_р, если постоянная Холла R_х = 3,8·10^-4 м³/Кл. Удельная проводимость полупроводника σ =110 (Ом·м)^-1.

Дано:
Найти:	nр, uр.

Решение: Концентрация дырок n_р связана с постоянной Холла, которая для полупроводников с решеткой типа алмаза, обладающих носителями только одного знака, выражается формулой:

(1)

где е - элементарный заряд.

Отсюда:

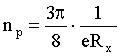(2)

Подставим числовые значения величин в формулу (2) и проведем вычисления:

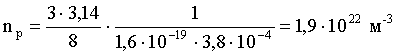
Удельная проводимость полупроводников выражается формулой:

(3)

где n_n и n_p - концентрации электронов и дырок,
u_n и u_p - их подвижности.

При отсутствии электронной проводимости первое слагаемое в скобках равно нулю, и формула (3) примет вид:

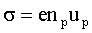
Отсюда искомая подвижность:

(4)

Подставим в (4) выражение n_р, описываемое формулой (2):

(5)

Подставим в (5) численные значения и проведем вычисления:

Ответ: ,

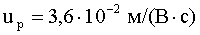
Дата добавления: 2015-06-04