Примеры решения задач по оптике

Задача 1. На каком расстоянии от предмета нужно поместить экран, чтобы плоско выпуклая линза с радиусом кривизны R = 20 см и показателем преломления n = 1,5 давала изображение предмета, увеличенное в 2 раза?

Дано:		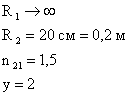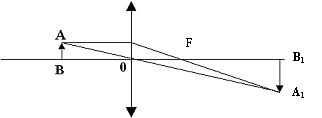Рис.6
Найти:	a

Решение: Построим изображение предмета (рис. 6). Из чертежа следует, что ΔАОВ ˜ ΔА₁ ОВ₁. Из подобия следует:

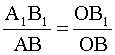
По условию задачи увеличение 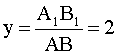. Следовательно:

(1)

Из принятых обозначений: ОВ = d, ОВ₁ = f. Тогда: f = 2d.
Определим оптическую силу линзы:

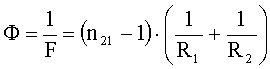(2)

Проведем вычисления:

Воспользуемся формулой тонкой линзы:

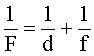(3)

Подставим (1) в (3):

Тогда: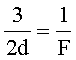

Найдем расстояние от предмета до линзы: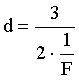

Вычислим:

Расстояние от предмета до экрана равно:

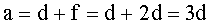
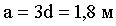
Ответ: а = 180 см.

Задача 2. На стеклянный клин падает нормально монохроматический свет (λ = 698 нм). Определить угол между поверхностями клина, если расстояние между соседними интерференционными минимумами в отраженном свете равно 2 мм.

Дано:		Рис.7
Найти:	φ

Решение: Параллельный пучок света, падая нормально к грани, отражается как от верхней (луч 1), так и от нижней (луч 2) грани клина (рис. 7). Лучи 1 и 2 когерентны между собой и интерферируют. Интерференционная картина представляет собой чередование темных и светлых полос. Темные полосы видны на тех участках клина, для которых оптическая разность хода кратна нечетному числу половины длины волны (условие минимума):

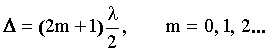
Оптическая разность хода в отраженном свете равна:

где i - угол падения луча. Так как по условию свет падает нормально, то i = 0 и sini = 0. Произвольной полосе с номером m соответствует толщина d_m, а (m+1) полосе соответствует толщина клина d_m+1. Запишем условие минимума для двух соседних темных полос:

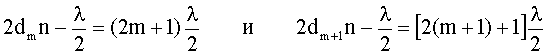
Отсюда: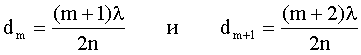

Тогда:

Из рисунка: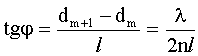

Вычислим: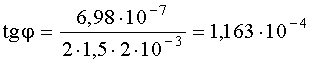

Тангенс мал, поэтому: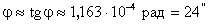

Ответ:

Задача 3. Измерение дисперсии показателя преломления оптического стекла дало n₁ = 1,528 для λ₁ = 0,434 мкм и n₂ = 1,523 для λ₂ = 0,486 мкм. Вычислить отношение групповой скорости к фазовой скорости для света с длиной волны 0,434 мкм.

Дано:
Найти:

Решение: Зависимость групповой скорости u от показателя преломления n и длины волны λ имеет вид:

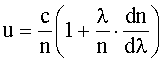(1)

где с - скорость света в вакууме.

Фазовая скорость определяется как 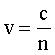(2)

Разделив выражение (1) на (2), получим:

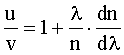
Средняя дисперсия:

Для длины волны λ₁ и средней дисперсии имеем:

Вычисления:

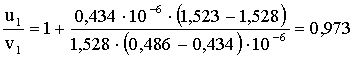
Ответ: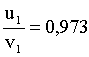

Дата добавления: 2015-06-04