Основные формулы. Пояснение к рабочей программе

При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебаний (в контрольной работе это задачи 301-310 для механических колебаний и задачи 311-320 для электромагнитных колебаний).

Нужно уметь представить гармонические колебания в виде вектора и пользоваться графическим методом сложения колебаний, т.е. строить векторную диаграмму (задачи 321-330). Важно представлять себе, что периодические процессы иной формы, чем гармонические, могут быть представлены в виде суперпозиции одновременно совершающихся гармонических колебаний с различными частотами, амплитудами и начальными фазами.

Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухания (в контрольной работе это задачи 331-340).

Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом (в контрольной работе это задачи 341-350).

При изучении темы "Волны" следует обратить внимание на картину мгновенного распределения смещений и скоростей частиц среды в бегущей волне. Здесь вводится понятие длины волны, скорости распространения волны, волнового числа (в контрольной работе это задачи 351-360).

Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна - это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

Уравнение гармонических колебаний: где х - смещение (отклонение) колеблющейся величины от положения равновесия; А - амплитуда; ω - круговая (циклическая) частота; t - время; α - начальная фаза; (ωt+α) - фаза.
Связь между периодом и круговой частотой:
Частота:
Связь круговой частоты с частотой: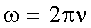
Периоды собственных колебаний пружинного маятника: где k - жесткость пружины; математического маятника: где l - длина маятника, g - ускорение свободного падения; колебательного контура: где L - индуктивность контура, С - емкость конденсатора.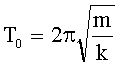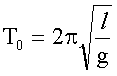
Частота собственных колебаний:
Сложение колебаний одинаковой частоты и направления: амплитуда результирующего колебания где А₁ и А₂ - амплитуды составляющих колебаний, α₁ и α₂ - начальные фазы составляющих колебаний; начальная фаза результирующего колебания
Уравнение затухающих колебаний: е = 2,71... - основание натуральных логарифмов.
Амплитуда затухающих колебаний: где А₀ - амплитуда в начальный момент времени; β - коэффициент затухания; t - время.
Коэффициент затухания: колеблющегося тела где r - коэффициент сопротивления среды, m - масса тела; колебательного контура где R - активное сопротивление, L - индуктивность контура.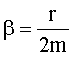
Частота затухающих колебаний ω:
Период затухающих колебаний Т:
Логарифмический декремент затухания:
Связь логарифмического декремента χ и коэффициента затухания β: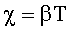
Амплитуда вынужденных колебаний где ω - частота вынужденных колебаний, f_о - приведенная амплитуда вынуждающей силы, при механических колебаниях:при электромагнитных колебаниях: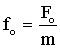
Резонансная частота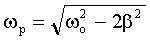
Резонансная амплитуда
Полная энергия колебаний: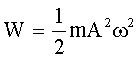
Уравнение плоской волны: где ξ - смещение точек среды с координатой х в момент времени t; k - волновое число:
Длина волны: где v скорость распространения колебаний в среде, Т - период колебаний.
Связь разности фаз Δφ колебаний двух точек среды с расстоянием Δх между точками среды: