Примеры решения задач по механике

Задача 1. Движение тела массой 2 кг задано уравнением: , где путь выражен в метрах, время - в секундах. Найти зависимость ускорения от времени. Вычислить равнодействующую силу, действующую на тело в конце второй секунды, и среднюю силу за этот промежуток времени.

Дано:
Найти: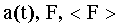

Решение: Модуль мгновенной скорости находим как производную от пути по времени:

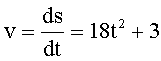
Мгновенное тангенциальное ускорение определяется как производная от модуля скорости по времени:

Среднее ускорение определяется выражением:

После подстановки:

Равнодействующая сила, действующая на тело, определяется по второму закону Ньютона:

Тогда

Ответ: a(t) = 36t, F = 144 H, = 72 H.

Задача 2. По наклонной плоскости, составляющей с горизонтом угол 30º, движется тело массой 5 кг. К этому телу с помощью нерастяжимой нити, перекинутой через блок, привязано тело такой же массы, движущееся вертикально вниз (рис. 1). Коэффициент скольжения между телом и наклонной плоскостью 0,05. Определить ускорение тел и силу натяжения нити.

Дано:		Рис. 1
Найти:

Решение: Покажем на рисунке силы, действующие на каждое тело. Запишем для каждого из тел уравнение движения (второй закон Ньютона):

В проекциях на выбранные оси координат:

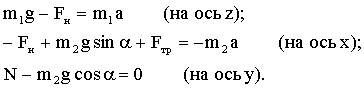
Учитывая, что 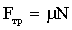, где , получим систему уравнений:

Вычтем из первого уравнения второе:

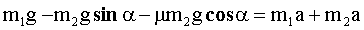
Искомое ускорение равно:

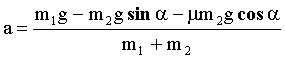
Вычислим ускорение а:

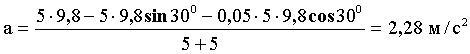
Силу натяжения найдем из первого уравнения системы:

Ответ: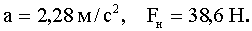

Задача 3. Найти линейные ускорения движения центров тяжести шара и диска, скатывающихся без скольжения с наклонной плоскости. Угол наклона плоскости равен 30º. Начальная скорость тел равна нулю.

Дано:		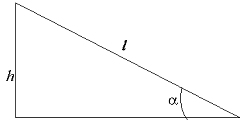Рис. 2
Найти: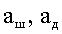

Решение: При скатывании тела с наклонной плоскости высотой h его потенциальная энергия переходит в кинетическую поступательного и вращательного движения. По закону сохранения энергии:

(1)

где I - момент инерции тела, m - масса.

Длина наклонной плоскости l связана с высотой соотношением (рис. 2):

(2)

Линейная скорость связана с угловой:

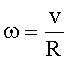(3)

После подстановки (2) и (3) в (1), получим:

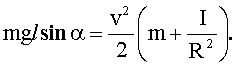(4)

Так как движение происходит под действием постоянной силы (силы тяжести), то движение тел - равноускоренное. Поэтому:

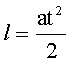(5)

и

(6)

Решая совместно (4), (5) и (6), получим:

(7)

Моменты инерции:

для шара:
для диска:

Подставляя выражение для момента инерции в формулу (7), получим:

для шара:
для диска: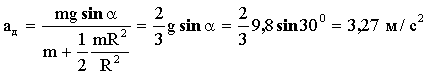

Ответ:

Дата добавления: 2015-06-04