Примеры решения задач по колебаниям и волнам

Задача 1. Материальная точка массой 10 г совершает гармоническое колебание с периодом Т=1 с. Определить амплитуду колебаний, максимальную скорость и ускорение колеблющейся точки, если полная энергия точки равна 0,02 Дж.

Дано:
Найти:

Решение: Уравнение гармонического колебания запишем в виде:

(1)

где х - смещение материальной точки от положения равновесия;
А - амплитуда;
ω - циклическая (круговая) частота;
t - время;
α - начальная фаза.

Скорость колеблющейся точки среды определяется как первая производная от смещения по времени:

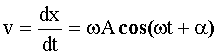
Максимальное значение скорости:

Ускорение точки определяется как производная от скорости по времени:

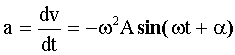
Максимальное значение ускорения:

Полная энергия складывается из кинетической и потенциальной энергии и равна максимальной потенциальной или максимальной кинетической энергии:

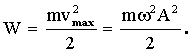
Круговая частота связана с периодом: . Тогда:

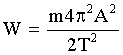
Из этого выражения найдем амплитуду:

Проверим размерность:

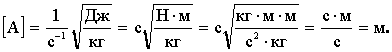
Произведем вычисления:

Ответ: А = 0,32 м, V_max = 2 м/с, a_max = 12,6 м/с²

Задача 2. Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных гармонических колебаний, данных уравнениями: x₁ = 0,02cos (5πt + π/2) м и x₂ = 0,03cos (5πt + π/4) м. Построить векторную диаграмму сложения амплитуд.

Дано: x₁ = 0,02cos (5πt + π/2)

x₂ = 0,03cos (5πt + π/4)

Найти: А, α. Дать векторную диаграмму.

Решение: Построить векторную диаграмму - это значит представить колебание в виде вектора, длина которого равна амплитуде колебаний, а угол наклона к оси абсцисс равен начальной фазе колебаний. При вращении вектора с угловой скоростью ω проекция его конца на ось будет совершать гармонические колебания.

Из условия задачи А₁=0,02 м = 2 см, α₁= π/2,

А₂=0,03 м = 3 см, α₂ = π/4.

Векторная диаграмма изображена на рисунке 5.

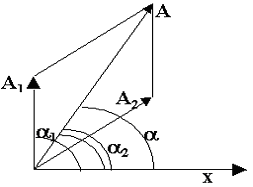
Рис. 5

Результирующую амплитуду найдем по теореме косинусов:

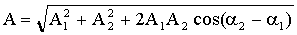
Начальная фаза результирующего колебания находится из формулы:

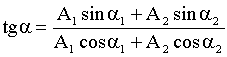
Вычисления:

Ответ: А = 4,6 м; α=62^о 46′.

Задача 3. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания χ = 1,6; начальная фаза равна нулю. Смещение точки в начальный момент времени равно 4,5 см. Написать уравнение колебаний и найти смещение точки в момент времени спустя период.

Дано: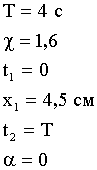
Найти:

Решение: Уравнение затухающих колебаний имеет вид:

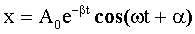(1)

где β - коэффициент затухания,
ω - частота затухающих колебаний.

Найдем ω:

Логарифмический декремент затухания связан с коэффициентом затухания: . Отсюда:

Подставим ω, β, α в (1) и найдем смещение:

Для начального момента времени при t = 0:

Уравнение колебаний имеет вид:

Смещение в момент :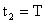

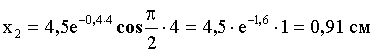
Ответ: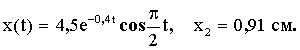

Дата добавления: 2015-06-04