БОБРУЙСК – 2007 г

Жидкости

Движение

Гидростатика.

№ п.п.	Название раздела	страница	К-во задач
	Гидростатика.
	Давление жидкости
	Закон Архимеда, плавание тел.
	Движение идеальной жидкости
	Течение вязкой жидкости

18. Гидростатика.

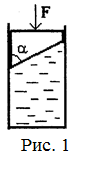
18.1. Жидкость в цилиндрическом сосуде сжимается поршнем. Сила, приложенная к поршню равна F, а площадь сечения сосуда S (рис. 1). Найти давление в жидкости. Атмосферным давлением, а также весом поршня и жидкости пренебречь. Изменится ли давление в жидкости, если нижняя часть поршня будет иметь более сложную форму? [ 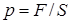; не изменится]

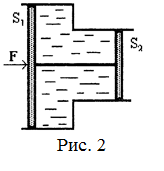18.2. Жидкость находиться между двумя поршнями площадью S ₁ и S ₂. На большой поршень действует сила F (рис. 2). Пренебрегая атмосферным давлением, найти давление в жидкости. [ ]

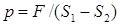18.3. В U – образной трубке находится ртуть. На сколько повысится уровень ртути в одном колене, если в другое налить столб воды высотой H = 136 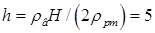мм? [ мм]

18.4. Три одинаковых вертикальных сосуда соединены в систему из трех сообщающихся сосудов. В систему залили ртуть. На сколько повысится уровень ртути в среднем сосуде, если в один из крайних налить слой воды высотой H ₁ = 102 мм, а в другой – слой воды высотой Н ₂ = 153 мм. [6,25 мм]

18.5. Два сообщающихся сосуда, площади сечения которых равны S ₁ и S ₂, закрыты невесомыми поршнями. Под поршнями находится жидкость с плотностью r. На сколько поднимется один из поршней, если на другой поставить гирьку массой m? [ ]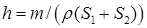

18.6. Концы U – образной трубки на l = 26 см выше уровня ртути. Какой максимальной высоты столб воды можно налить в одно из колен трубки? [ 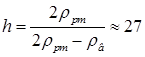см]

18.7. На первом этаже здания давление воды в водопроводе равно 1 атм. На каком этаже вода из крана уже не течет, если высота каждого этажа равна 3 м? [на пятом]

18.8. В цилиндрический сосуд налили две несмешивающиеся жидкости в равных по массе количествах. Плотности жидкостей равны r₁ = 1 г/см³ и r₂ = 0,9 г/см³, а общая высота слоя жидкостей равна Н = 40 см. Найти давление жидкостей на дно сосуда. Атмосферное давление не учитывать. [ 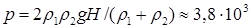Па]

18.9. Тело плавает в воде, погрузившись в нее на 3/4 своего объема. Найти плотность материала тела. [750 кг/м³]

18.10. Тело плавает в воде, погрузившись в нее на a = 0,75 своего объема. Какая часть объема тела будет погружена в спирт, плотность которого равна r _сп = 0,8 г/см³? [ ]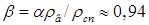

18.11. Два тела: одно плотностью r₁ = 1,5 г/см³ и объемом V ₁ = 0,5 см³; второе плотностью r₂ = 0,5 г/см³ и объемом V ₂ = 1,5 см³ связали вместе и опустили в воду. Какая часть их общего объема будет погружена в воду? [ ]

18.12. Вес тела в жидкости с плотностью r₁ равен P ₁, a в жидкости с плотностью r₂ равен P ₂. Найти плотность тела. [ ]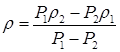

18.13. Тело весом P, погруженное в жидкость с плотностью r₁, весит P ₁, а погруженное в жидкость с неизвестной плотностью r₂, весит Р ₂. Найти r₂. [ ]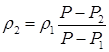

18.14. Тело плавает на границе двух несмешивающихся жидкостей с плотностями r₁ и r₂ (r₁ < r₂) При этом отношение объемов, погруженных в верхнюю и в нижнюю жидкости, равно V ₁/ V ₂ = n. Определить плотность тела. [ ]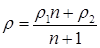

18.15. В цилиндрической банке высота уровня воды составляет h _o = 15 см. Когда в нее опустили плавать пустую латунную чашку, уровень воды поднялся на D h = 2,1 см. Какова будет высота уровня воды в банке, если чашку утопить? Плотность латуни равна r _л = 8,4 г/см³. [ 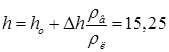см]

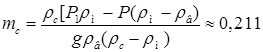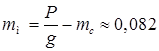18.16. Кусок сплава меди и серебра весит в воздухе P = 2,94 Н, а в воде – P ₁ = 2,65 Н. Сколько серебра и меди в куске? Плотности: меди – r _м = 8,9 г/см³, серебра – r _с = 10,5 г/см³. [ кг; кг]

18.17. Посередине большого озера просверлили прорубь. Толщина льда оказалась 8 м. Какой наименьшей длины веревку необходимо взять, чтобы зачерпнуть воду из проруби? [0,8 м]

18.18. На границе раздела двух несмешивающихся жидкостей с плотностями r₁ и r₂ плавает тело с плотностью r (r₁ < r < r₂). Какая часть объема тела находится в верхней жидкости? [ ]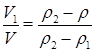

18.19. Бревно длиной L = 3,5 м и поперечным сечением S = 0,04 м² плавает в воде. Какую наибольшую массу может иметь человек, чтобы бревно не утонуло, когда человек встанет на него? Плотность дерева r _д = 500 кг/м³. [ 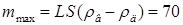кг]

18.20. Тело массой m, утонувшее в жидкости с плотностью r₁, давит на дно с силой F. Какая часть тела будет погружена в жидкость с плотностью r₂, на поверхности которой оно плавает? [ ]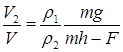

18.21. Шар массой 1 кг наполовину погружен в воду и давит на дно с силой 8 Н. Найти плотность материала шара. [2500 кг/м³]

18.22. Шар плавает в воде, погрузившись в нее на 3/4 своего объема. Какая часть шара должна выступать из воды, чтобы сила его давления на дно равнялась половине силы тяжести шара? [0,625]

18.23. Льдина площадью 2 м² плавает в воде. Когда на нее встал человек массой 70 кг высота верхнего края льдины над водой уменьшилась вдвое. Какова толщина льдины? [0,7 м]

18.24. Каким должен быть объем полости железного буя, для того чтобы он мог плавать на поверхности воды? Объем буя V, плотности железа и воды – r _ж и r _в. [ ]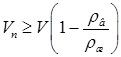

18.25. Для взятия пробы грунта на дно океана на стальном тросе опускается прибор. Найти предельную глубину погружения, если предел прочности стали на разрыв s= 4,8×10Н/м². Плотность стали r _ст = 7800 кг/м³. Массой прибора пренебречь. [ 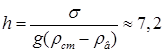км]

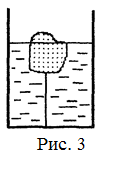
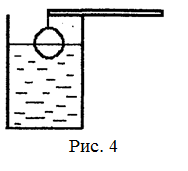18.26. В цилиндрическом стакане с водой плавает льдинка, привязанная нитью ко дну (рис. 3). Когда льдинка растаяла уровень воды понизился на D h. Каково было начальное натяжение нити? Площадь дна стакана равна S. [ ]

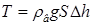18.27. На чашках погруженных в воду равноплечных весов находятся алюминиевый и железный шары одинаковой массы m. Определить массу сплошного шара из меди, который необходимо добавить для восстановления равновесия. Плотности алюминия, железа и меди: r _а, r _ж и r _м. [ ]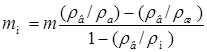

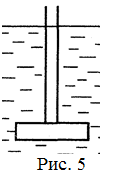18.28. К концу однородной палочки массой m = 4 г подвешен на нити шар радиусом r = 0,5 см. Палочка лежит на краю стакана (рис 4). В равновесии шар погружен в воду ровно наполовину. В каком отношении делится палочка точкой опоры? Плотность шара r = 2,7 г/см³. [ ]

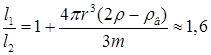18.29. В бак с жидкостью опущена длинная трубка диаметром d, к которой снизу плотно прилегает цилиндрический диск толщиной h и диаметром D (рис. 5). Плотность диска r _д больше плотности жидкости r _ж. На какой глубине диск оторвется, если трубку медленно вытаскивать из жидкости? [ ]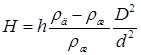

18.30. Деревянный шарик, падая с высоты h ₁ = 60 см, погрузился в воду на глубину h ₂ = 60 см. На какую высоту выпрыгнет из воды этот шарик? Сопротивление воды считать постоянным, плотность дерева равна r_д = 0,8 г/см³. [ 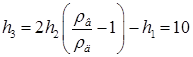см]

18.31. Два цилиндрических сообщающихся сосуда частично заполнены водой. В один из сосудов опускают тело массой m, которое плавает на поверхности. На сколько повысится уровень воды в сосудах? Площади сечения сосудов равны S ₁ и S ₂. [ ]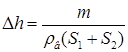

18.32. В цилиндрический сосуд массой M и площадью дна S налита вода до уровня h. Вода сверху закрыта поршнем, в котором имеется крючок. Каким будет давление под поршнем, если сосуд приподнять за этот крючок (рис. 6)? Атмосферное давление равно p_a. [ ]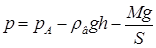

18.33. Первый шарик всплывает в воде с постоянной установившейся скоростью v _o. Второй такой же по размеру шарик тонет в воде с постоянной установившейся скоростью 2 v _o. С какой постоянной установившейся скоростью будут тонуть эти шарики, если связать их нитью? Считать, что сила сопротивления пропорциональна скорости. [ 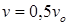; при установившемся движении сила тяжести, сила Архимеда и сила сопротивления уравновешивают друг друга]

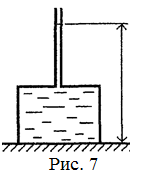
18.34. Цилиндрический сосуд массой М и высотой h поставлен дном вверх на ровную горизонтальную резиновую поверхность. В дне сосуда имеется маленькое отверстие, в которое вставлена длинная тонкая трубка (рис. 7). Через трубку сосуд заполняется водой. До какой максимальной высоты можно в трубку налить воду? Площадь дна сосуда равна S. [ 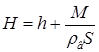; вода начнет приподнимать сосуд и вытекать из-под него, когда сила давления воды снизу вверх на дно сосуда 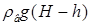станет равна силе тяжести сосуда Mg ]

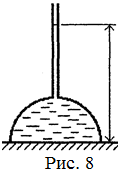
18.35. Полая тонкая полусфера массой М и радиусом R лежит на ровной горизонтальной резиновой поверхности. В верхней части полусферы имеется маленькое отверстие, в которое вставлена длинная тонкая трубка (рис. 8). Через трубку полусфера заполняется водой. До какой максимальной высоты можно налить в трубку воду? [ 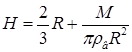; Сила, с которой полусфера и вода давят на поверхность, равна: 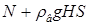, где N – сила давления полусферы; 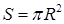. С другой стороны, эта сила равна суммарной силе тяжести системы: 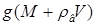– где V – объем полусферы (массу воды в трубке не учитываем). Когда вода начнет приподнимать полусферу и вытекать из-под нее, сила давления полусферы на поверхность станет равна нулю.]

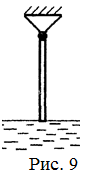
18.36. Легкий стержень свободно висит, касаясь нижним концом поверхности воды. Верхний конец стержня закреплен шарнирно (рис. 9). Вода начинает прибывать и ее уровень поднимается. Как зависит угол отклонения стержня от вертикали от высоты поднятия уровня воды? Длина стержня равна l, плотность стержня в n раз меньше плотности воды. Высота поднятия уровня воды отсчитывается от ее начального уровня. [ ]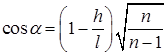

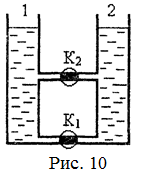
18.37. Два цилиндрических сообщающихся сосуда соединены двумя трубками с кранами (рис. 10). Сначала краны открыты и в сосуды наливают жидкость. Затем краны закрывают и жидкость в сосуде 2 нагревают, в результате чего уровень жидкости в этом сосуде слегка повысился. Куда потечет жидкость, если открыть: а) кран K ₁; б) кран К ₂; в) оба крана? [а) Никуда; б) из 2 в 1; в) возникает циркуляция: внизу из 1 в 2, вверху из 2 в 1]

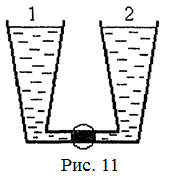18.38. Два расширяющихся кверху сосуда соединены трубкой с краном и заполнены жидкостью (рис. 11). Сначала кран открыт. Затем его закрывают и жидкость в сосуде 2 нагревают, в результате чего уровень жидкости в нем слегка повысился. Куда потечет жидкость, если кран открыть? [из 1 в 2]

18.39. Два одинаковых по размеру шарика массами m ₁ и m ₂ (m ₁ < m ₂) связаны нитью и тонут в воде с постоянной скоростью. Определить силу натяжения нити. [ ]

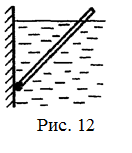
18.40. Однородная палочка, шарнирно прикрепленная к стенке бассейна, высовывается из воды на 0,1 своей длины (рис. 12). Найти плотность материала палочки. [810 кг/м³]

18.41. Какую работу необходимо совершить, чтобы утопить плоскую льдину массой M = 1000 кг и площадью S = 2 м²? [ 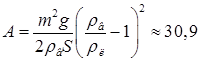Дж]

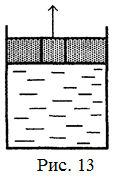18.42. В цилиндрический сосуд с площадью дна S налита жидкость плотностью r. Сверху непосредственно на жидкости лежит массивный поршень с пробкой (рис. 13). Поршень и пробка сделаны из одного материала, имеют одинаковую толщину h и могут двигаться без зазора и без трения. Какую работу надо совершить, чтобы вытащить пробку? Площадь пробки равна S ₁. [ 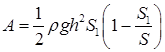; работа равна разности потенциальных энергий системы в конечном и начальном состояниях. Если за ноль потенциальной энергии взять нижнюю грань поршня в конечном состоянии, то начальная и конечная энергии системы равны: 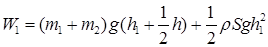и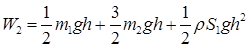

где m ₁ и m ₂ – масса поршня и пробки; h ₁ – высота на которую опустился поршень при вытаскивании пробки. Дополнительные соотношения: .]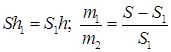

13.43. До какой высоты надо налить воду в цилиндрический сосуд радиусом R, чтобы силы давления воды на дно и на боковую поверхность были равны? [ h = R ]

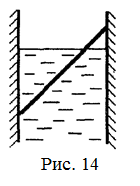
18.44. Однородная деревянная рейка массой m и длиной l плавает в воде между двумя вертикальными стенками (рис. 14). Расстояние между стенками d < l, а отношение плотностей рейки и воды равно a < 1. С какой силой рейка давит на стенки? Трения нет. [ ]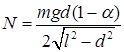

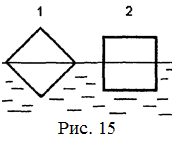
18.45. Кубик, сделанный из материала, плотность которого вдвое меньше плотности воды, плавает в воде. Какое из двух показанных положений кубика будет устойчивым (рис. 15)? [Первое; устойчивым будет положение, в котором потенциальная энергия системы меньше. Так как энергия кубика в обоих положениях одинакова, то меньшей энергией будет обладать то положение, в котором потенциальная энергии воды меньше. Но потенциальная энергия воды равна ее энергии без погруженного кубика минус энергия воды в объеме погруженной части кубика. Значит устойчивым будет положение в котором центр масс погруженной части кубика выше. Центр масс однородного треугольника находится в точке пересечения медиан.]

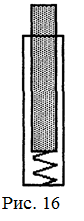
18.46. Внутри вертикального узкого стакана стоит вертикальная пружина, длина которой равна высоте стакана. Если в стакан поставить однородный стержень, длина которого тоже равна высоте стакана, то четвертая часть его будет высовываться из стакана (рис. 16). Если в стакан доверху налить воду, то из стакана будет высовываться половина стержня. Найти плотность материала стержня. [ кг/м³]

18.47. Однородный стержень плотностью r плавает на границе раздела двух несмешивающихся жидкостей с плотностями r₁ и r₂ (r₁ < r < r₂). При каком соотношении между плотностями устойчивым положением стержня будет вертикальное? [Вертикальное положение не может быть устойчивым]

18.48. В воде плавает доска массой М. Плотность доски вдвое меньше плотности воды. Когда на конец доски села лягушка, верхний край доски с этого конца опустился как раз до уровня воды. Найти массу лягушки. [ ]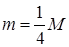

18.49. Воздушный шар опускается с постоянной скоростью. Когда из него выбросили груз массой m, он начал подниматься с той же постоянной скоростью. Найти силу сопротивления воздуха при этой скорости. [ ]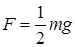

18.50. Воздушный шар опускается с постоянной скоростью. Общая масса оболочки и груза равна М, объем оболочки – V, плотность воздуха – r _в, плотность газа в оболочке – r. Какой массы груз надо выбросить, чтобы шар начал подниматься с той же постоянной скоростью? Считать, что сила сопротивления пропорциональна скорости. [ ]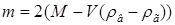

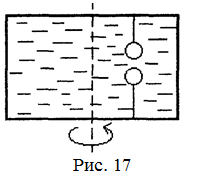18.51. В вертикальном цилиндрическом сосуде, доверху заполненном водой и закрытом крышкой, на нитях висят два шарика: сверху стальной; снизу пробковый (рис. 17). Как будут вести себя шарики, если сосуд начнут медленно раскручивать вокруг его оси? [верхний шарик будет отклоняться от оси, а нижний – к оси]

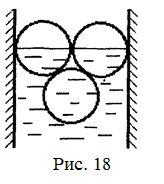18.52. Три одинаковых бревна плавают в воде между вертикальными стенками канала. Расстояние между стенками слегка больше удвоенного диаметра бревен, а верхние бревна погружены в воду ровно наполовину (рис. 18). С какой силой бревна давят на стенки канала, если масса каждого бревна равна m? Трения нет. [ ]

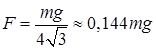18.53. Большая плоская льдина плавает в воде. В льдине просверлили прорубь площадью S = 300 см². Вода в проруби оказалась на глубине h = 10 см. Какое максимальное количество масла можно налить в прорубь? Плотность масла равна r _м = 800 кг/м³. [ 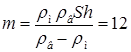кг]

18.54. Два шарика, сделанные из одного материала, имеют объемы: V и 3 V. Шарики связали невесомой нитью, перекинутой через неподвижный блок, и отпустили над поверхностью воды. Когда один из шариков погрузился в воду ускорение системы изменилось на противоположное. Найти плотность материала шариков. Сопротивление воды и трение не учитывать. [ 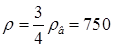кг/м³]

18.55. Тело массой m тонет в воде с ускорением a. С какой силой его надо тянуть вверх, чтобы оно поднималось с тем же ускорением? Сопротивление не учитывать. [ ]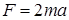

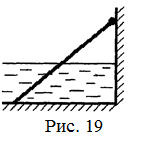
18.56. Тонкий однородный стержень длиной l = 1 м, сделанный из материала с плотностью r = 0,91 г/см³, шарнирно прикреплен к стенке бассейна и опирается на дно так, что составляет угол a = 60° с вертикалью (рис. 19). В бассейн начинают наливать воду. При какой высоте уровня воды стержень перестанет давить на дно? [ 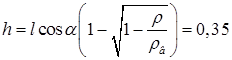м]

18.57. Цилиндрический сосуд радиусом R, заполненный жидкостью с плотностью r, вращается вокруг своей вертикальной оси с угловой скоростью w. В сосуде находится маленький шарик радиусом r и плотностью 2r (r << R). С какой силой шарик давит на боковую поверхность сосуда? [ ]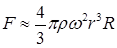

18.58. Аквариум с водой на колесиках скатывается с наклонной плоскости без трения. Как располагается уровень поверхности воды при установившемся скатывании? [Параллельно наклонной плоскости]

Дата добавления: 2015-06-04