Плавание. Закон Архимеда

20.1. Определите давление жидкости на нижнюю поверхность плавающей шайбы сечения S и массы m. [ ]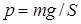

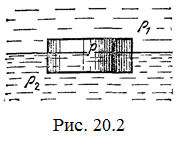20.2. На границе раздела двух жидкостей плотностей r₁ и r₂ плавает шайба плотности r (r₁ < r < r₂). Высота шайбы h. Определите глубину ее погружения во вторую жидкость. [ x = h(r-r₁)/(r₂ -r₁). Ответ исправлен 19.11.2010]

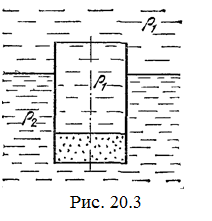
20.3. Тонкостенный стакан массы т вертикально плавает на границе раздела жидкостей плотностей r₁ и r₂. Определите глубину погружения стакана в нижнюю жидкость, если дно стакана имеет толщину h и площадь S и стакан заполнен жидкостью плотности r_l. [ ]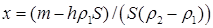

20.4*. В жидкости плотности r_o плавает прямоугольный параллелепипед из ма 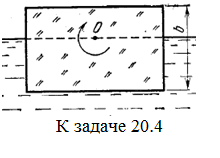териала плотности r. Высота параллелепипеда b, ширина и длина a. При каком отношении a к b его положение устойчиво? [Если при повороте параллелепипеда вокруг оси, проходящей через точку O, центр тяжести системы жидкость – параллелепипед повышается, положение параллелепипеда устойчиво. Это условие выполняется при ]

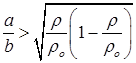20.5. Деревянный куб с ребром 0,5 м плавает в озере, на ²/₃ погруженный в воду. Какую минимальную работу нужно совершить, чтобы утопить куб? [ A = 32,5 Дж]

20.6. Кусок железа весит в воде 1 H. Определите его объем. Плотность железа 7,8 г/см³. [ V = 147 см³]

20.7. Тело в воде весит в три раза меньше, чем в воздухе. Чему равна плотность тела? [r = 1,5 г/см³]

20.8. К коромыслу весов подвешены два груза равной массы. Если один из грузов поместить в жидкость плотности r₁, а другой в жидкость плотности r₂, то равновесие сохранится. Найдите отношение плотностей грузов. [ ]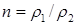

20.9*. В сообщающиеся сосуды диаметров d ₁и d ₂налита жидкость плотности r. На сколько поднимется уровень жидкости в сосудах, если в один из сосудов положить тело массы m из материала, плотность которого меньше r? [ ]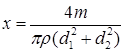

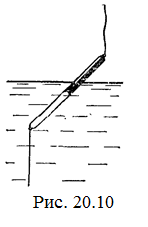
20.10. Определите натяжение нижней лески у поплавка, изображенного на рисунке, если поплавок погружен в воду на ²/₃ своей длины. Масса поплавка 2 г. [ F = 9,8×10^–3 H]

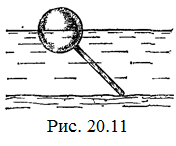
20.11. С какой силой давит тяжелая палочка на дно водоема, если жестко связанный с палочкой пустотелый шарик радиуса r погрузился в жидкость наполовину? Плотность жидкости r, длина палочки l. [ ]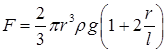

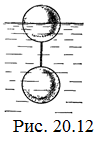
20.12. Определите натяжение нити, связывающей два шарика объема 10 см³, если верхний шарик плавает, наполовину погрузившись в воду. Нижний шарик в три раза тяжелее верхнего. [ 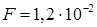H]

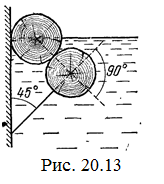
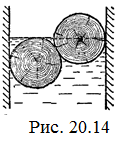
20.13. Два одинаковых бревна расположены так, как показано на рисунке. Нижнее бревно привязано к вертикальной стенке тросами, составляющими с ней угол 45°. Верхнее бревно наполовину погружено в воду. Определите плотность бревен. [r = 2/3 г/см³]

20.14. Определите силу давления бревен массы т на стенки канала. Верхнее бревно погружено в воду наполовину, а нижнее касается верхним участком поверхности воды. [ ]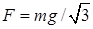

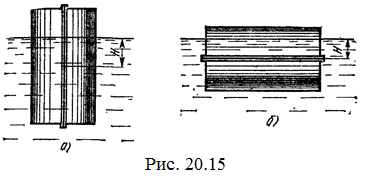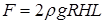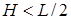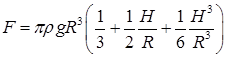20.15*. Как зависит сила, прижимающая два одинаковых полуцилиндра плавающего батискафа, от глубины его погружения Н,если плоскость соприкосновения полуцилиндров: а) вертикальна; б) горизонтальна? Радиус батискафа R,длина L,плотность жидкости r. [ a) , если ; , если H > L /2. б) , если H < R; 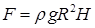, если H > R ]

20.16*. Докажите, что сила, с которой прижимаются половины сферического батискафа друг к другу, не зависит от наклона плоскости соприкосновения полусфер батискафа, если он полностью погружен в жидкость.

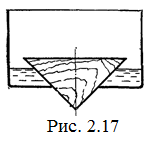20.17.Коническая пробка высоты 10см с углом при вершине 90° перекрывает отверстие радиуса 5 см. Чему должна быть равна масса этой пробки, чтобы она не всплывала при изменении уровня воды в сосуде? [ m = 520 г]

20.18*.Решите задачу 20.17 при условии, что отверстие радиуса r перекрывает шар радиуса R, а плотность жидкости равна r. [ ]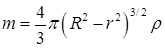

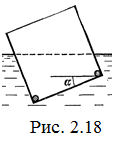
20.19*.Наклон кубической коробки, наполовину погруженной в жидкость, равен а. Определите массу каждого из двух противоположных ребер коробки. Массой остальных частей коробки пренебречь. Плотность жидкости r, длина ребер коробки a. [ ; ]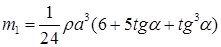

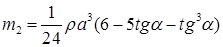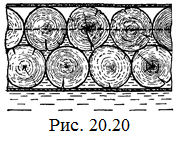
20.20*. Определите минимальное натяжение двух канатов, связывающих широкий плот, состоящий из двух слоев бревен. Масса каждого бревна т. Верхний слой бревен погружен в воду наполовину. [ ]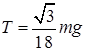

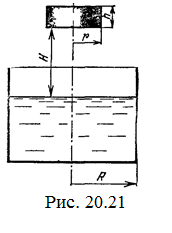
20.21.В цилиндр радиуса R,частично заполненный жидкостью, падает цилиндрическая пробка радиуса r и высоты h. Начальная высота нижнего торца пробки над уровнем жидкости R, начальная скорость равна нулю. Какое количество тепла выделится к моменту окончания движения жидкости и пробки? Плотность пробки r, плотность жидкости r_o > r.

[ ]

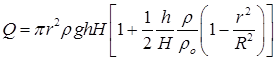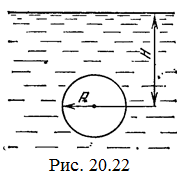
20.22. Какое количество тепла выделится в водоеме при всплывании в нем воздушного пузыря радиуса R = 0,1 м с глубины H = 10 м? Плотность воды r. [ 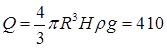Дж]

20.23. Какую минимальную работу нужно произвести, чтобы вытащить со дна моря на борт судна батискаф радиуса 2 м? Масса батискафа 35 т, глубина моря 100 м, высота борта судна 3 м. [ A = 283 кДж]

20.24*.Для создания искусственной тяжести цилиндрический космический корабль радиуса R вращается вокруг своей оси с угловой скоростью w. Бассейн в корабле имеет глубину H, а дном бассейна служит боковая стенка корабля.

а) Сможет ли космонавт плавать в этом бассейне? Опишите особенность космического бассейна. Определите плотность плавающей в бассейне палочки длины l < H, если из воды выступает ее верхняя часть длины D. [ a) Сможет. ]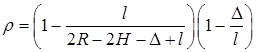

б) В бассейне можно наблюдать следующее интересное явление: два шара разной плотности, связанные нитью, в зависимости от «глубины» движутся или к свободной поверхности, или к стенке космического корабля, если плотность одного шара больше, а другого меньше плотности воды. Объясните это явление.

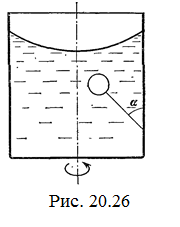20.25. Цилиндрический сосуд радиуса R,заполненный жидкостью плотности r_o, вращается с угловой скоростью со вокруг своей оси. В сосуде находится шарик радиуса r и плотности r > r_o. Найдите силу, с которой шарик давит на боковую стенку сосуда. [ ]

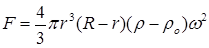20.26. Цилиндрический сосуд радиуса R,частично заполненный жидкостью, вращается вместе с жидкостью вокруг своей оси. К боковой стенке сосуда на нити длины l привязан воздушный шарик радиуса r;во время вращения нить образует со стенкой угол a. Определите угловую скорость вращения. Поле тяжести направлено вдоль оси сосуда. [ ]

Дата добавления: 2015-06-04