
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение. Краткое содержание: Введение
|
|
|
|
Лекция 1
Краткое содержание: Введение. Элементы векторной алгебры: понятие вектора, свойства векторов, правые и левые системы координат, скалярное и векторное произведение двух векторов.
Нас с вами окружают различные материальные объекты, которые взаимодействуют между собой. В результате воздействия одного материального объекта на другой, изменяется их положение в пространстве, меняется их форма и размеры.
Материальными объектами являются твердые и деформируемые тела, жидкости и газы. Эти объекты так же называются сплошной средой.
Изучением поведения материальных объектов при их взаимодействии между собой занимается наука под названием «механика сплошной среды», которая состоит из нескольких разделов (наук).
Аэро- и гидромеханика – это разделы механики сплошной среды, которые изучают равновесие и движение газообразных и жидких сред соответственно и их взаимодействие между собой и с твёрдыми телами.
Механика деформируемого твердого тела – это наука, которая изучает свойства деформируемых тел.
Теоретическая механика – это наука, в которой изучаются механические движения материальных объектов.
Механическое движение – это перемещение материальных объектов в пространстве с течением времени без рассмотрения физических свойств этих объектов и их изменения в процессе движения.
Теоретическая механика занимает центральное место среди других дисциплин, так как в ней определяются все основные понятия механики: сила, момент и импульс силы, скорость и ускорение точки и другие.
Теоретическая механика изучает только вещественные формы материальных объектов. Элементарные частицы и различные поля не являются предметом изучения в теоретической механике.
Теоретическую механику называют еще классической механикой или механикой Ньютона. Движение материальных объектов происходит в пространстве и во времени. Пространство является трехмерным пространством Эвклида.
Традиционно теоретическая механика делится на три части: статику, кинематику и динамику. Изучение теоретической механики обычно происходит в такой же последовательности. Главной и наиболее трудной частью ТМ является динамика.
Элементы векторной алгебры
Большинство величин, рассматриваемых в теоретической механике, являются векторными величинами, поэтому мы вспомним, что такое вектор, свойства векторов и операции над ними. Для определенности рассматриваем прямоугольную декартову систему координат.
Понятие вектора.
Вектор это направленный отрезок, он характеризуется длиной и направлением.
Операции над векторами. Вектора можно складывать и умножать на число.
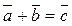 сумма двух векторов есть вектор
сумма двух векторов есть вектор
 произведение вектора на действительное число есть вектор
произведение вектора на действительное число есть вектор
 существует нулевой вектор
существует нулевой вектор
|
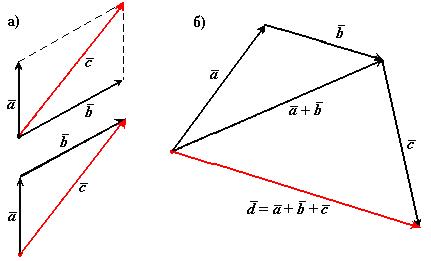
| Рис. 1.1 |
В математике все вектора являются свободными, их можно переносить параллельно самим себе.
В сумме двух векторов (см. рис. 1.1а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (см. рис. 1.1б) получаем, что суммой нескольких векторов является вектор, замыкающий ломаную линию, состоящую из слагаемых векторов.
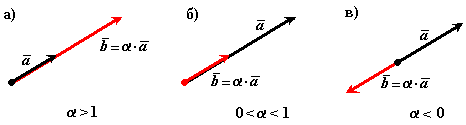
|
| Рис. 1.2 |
Операции над векторами подчиняются следующим законам (см. рис. 1.2):
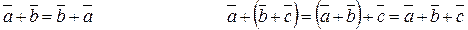


Правые и левые системы координат.
Декартовы системы координат делятся на два вида: правые и левые.
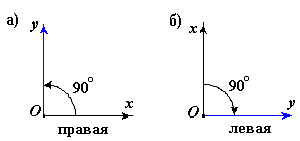
| Рассмотрим декартовы системы координат на плоскости (см. рис. 1.3).
При повороте оси 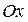 правой системы координат на правой системы координат на  против часовой стрелки она совпадает с осью против часовой стрелки она совпадает с осью 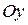 . .
| |
| Рис. 1.3 | ||

| Рассмотрим декартовы системы координат в пространстве (рис. 1.4).
При повороте оси 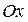 правой системы координат вокруг оси правой системы координат вокруг оси 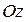 на на  против часовой стрелки она совпадает с осью против часовой стрелки она совпадает с осью 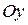 . .
| |
| Рис. 1.4 | ||
Длина, проекции и направляющие косинусы вектора
В дальнейшем будем рассматривать правую декартову систему координат.
Единичные вектора вдоль осей 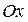 ,
, 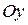 и
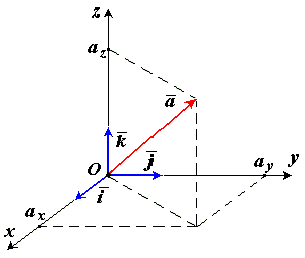
и 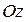 образуют систему единичных (или базисных) векторов. Любой вектор, имеющий начало в точке O, можно представить как сумму
образуют систему единичных (или базисных) векторов. Любой вектор, имеющий начало в точке O, можно представить как сумму  числа
числа 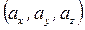 - это проекции вектора
- это проекции вектора  на оси координат (см. рис. 1.5).
на оси координат (см. рис. 1.5).
Длина (или модуль) вектора 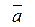 определяется формулой
определяется формулой  и обозначается
и обозначается  или
или  .
.
| Если вектор имеет начало не в точке О (начале координат), то проекцией вектора на ось является скалярная величина (число), которая равна разности координат конца и начала этого вектора. Для определения коорди-нат опускаем перпендикуляры, из начала и конца вектора на эту ось. (см. рис. 1.6). |
| Рис. 1.5 |

|
| Рис. 1.6 |
Направляющими косинусами 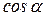 ,
, 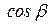 ,
, 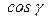 вектора называются косинусы углов между вектором и положительными направлениями осей
вектора называются косинусы углов между вектором и положительными направлениями осей 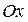 ,
, 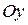 и
и 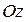 соответственно:
соответственно:
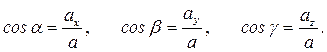
Любая точка пространства с координатами  может быть задана своим радиус-вектором
может быть задана своим радиус-вектором
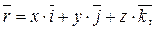
Координаты  это проекции вектора
это проекции вектора  на оси координат.
на оси координат.
Скалярное произведение двух векторов
Имеется два вектора 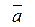 и
и 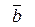 .
.  ,
, 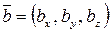 .
.

| Результатом скалярного произведения двух векторов 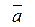 и и 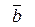 является скалярная вели-чина (число). Записывается как является скалярная вели-чина (число). Записывается как 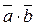 или или  . Скалярное произведение двух векторов равно . Скалярное произведение двух векторов равно  . .
|
| Рис. 1.7 |
Свойства скалярного произведения:
 ;
;
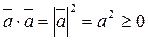 ;
;
 ;
;
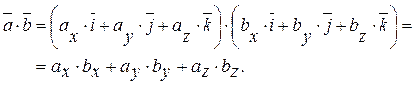
Векторное произведение двух векторов
Имеется два вектора 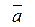 и
и 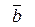 .
.  ,
, 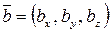 .
.

| Результатом векторного произведения двух векторов 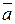 и и 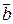 является вектор является вектор 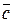 . Записывается как . Записывается как 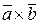 или или  .
Векторное произведение двух векторов это вектор .
Векторное произведение двух векторов это вектор 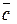 , перпендикулярный к обоим этим векторам, и направленный так, чтобы с его конца поворот вектора , перпендикулярный к обоим этим векторам, и направленный так, чтобы с его конца поворот вектора 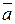 к вектору к вектору  был виден против часовой стрелки. был виден против часовой стрелки.
|
| Рис. 1.8 |
Длина (или модуль) векторного произведения равна  .
.
Свойства векторного произведения:

Векторное произведение двух векторов вычисляется через их проекции следующим образом:

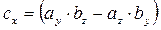 ;
;
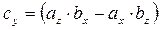 ;
;
 .
.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 440; Нарушение авторских прав?; Мы поможем в написании вашей работы!