Формулы для моментов силы относительно осей координат

Если сила 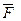задана своими проекциями 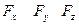на оси координат и даны координаты 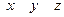точки приложения этой силы, относительно осей координат, то моменты силы относительно осей координат вычисляется следующим образом:

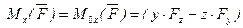
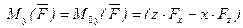
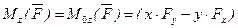
Лекция 4

Краткое содержание: Пара сил. Теорема о сумме моментов пары сил. Теорема об эквивалентности пар сил. Теорема о переносе пары сил в параллельную плоскость. Теорема о сложении пар сил. Условия равновесия пар сил.

ПАРА СИЛ

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Плоскостью действия пары сил называется плоскость в которой расположены эти силы.

Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.

Моментом пары сил называется вектор 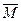, модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.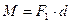

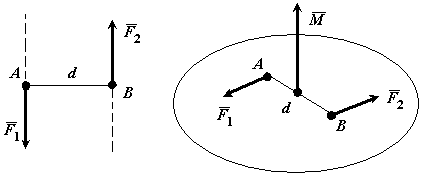Рис. 4.1

Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.

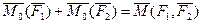
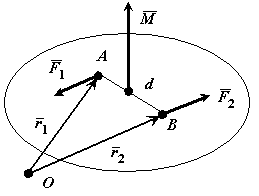Рис. 4.2

Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

Выводы:

1. Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.

2. У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.

Теорема о переносе пары сил в параллельную плоскость. Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.

Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.

Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.

Теорема о сложении пар сил. Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.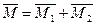

Условия равновесия пар сил.

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

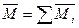
Теорема. Для равновесия пар сил, приложенных к твердому телу, необхо-димо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.

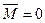
Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.

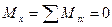
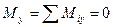
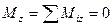
Лекция 5

Краткое содержание: Приведение силы к заданному центру. Приведение системы сил к заданному центру. Условия равновесия пространственной системы параллельных сил. Условия равновесия плоской системы сил. Теорема о трех моментах. Статически определимые и статически неопределимые задачи. Равновесие системы тел.

ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ

Приведение силы к заданному центру.

Равнодействующая системы сходящихся сил непосредственно находится с помощью сложения сил по правилу параллелограмма. Очевидно, что аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку.

Теорема о параллельном переносе силы. Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.

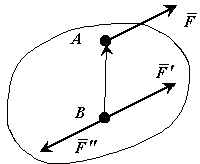
Пусть сила 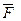приложена в точке A. Действие этой силы не изменяется, если в точке B приложить две уравновешенные силы. Полученная система трех сил представляет собой силу 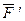равную 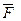, но приложенную в точке В и пару 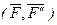с моментом 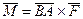. Процесс замены силы 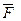силой 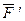и парой сил 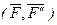называется приведением силы 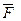к заданному центру В.

Приведение системы сил к заданному центру.

Основная теорема статики (Пуансо).

Любую произвольную систему сил, действующую на твердое тело, можно в общем случае привести к силе и паре сил. Этот процесс замены системы сил одной силой и одной парой сил называется приведением системы сил к заданному центру.

Главным вектором системы сил называется вектор, равный векторной сумме этих сил.

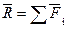
Главным моментом системы сил относительно точки О тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки.

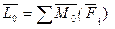
Формулы для вычисления главного вектора и главного момента

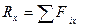
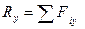
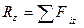
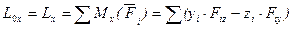
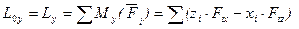
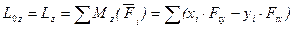
Формулы для вычисления модуля и направляющих косинусов

главного вектора и главного момента

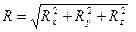
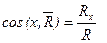
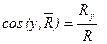
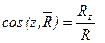
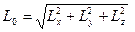
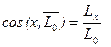
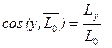
Условия равновесия системы сил.

Дата добавления: 2015-06-04