Свойства силы и пар сил

Статика

В статике изучают свойства сил и определяют условия равновесия тел.

Сила есть мера механического действия одного тела на другое, которая проявляется в виде деформации или изменения движения тела.

Сила есть приложенный вектор, изображаемый из точки приложения силы, определяемый двумя векторами: вектором и радиус-вектором точки её приложения.

Силу можно задавать в декартовой системе отсчета шестью скалярами: тремя проекциями силы на оси координат X, Y, Z и тремя координатами x,y,z точки приложения силы.

Силу, приложенную к абсолютно твердому телу можно считать скользящим вектором, т.е. силу можно перемещать вдоль линии её действия, минуя точку приложения, поскольку известно, что при этом механическое действие силы на тело, способность разгонять и раскручивать тело не меняются. Параллельный перенос силы не допустим - при переносе силы на параллельную линию, изменяется её вращательная способность. Силу можно раскладывать на составляющие, т.е. – заменять несколькими силами, приложенными в прежней точке тела.

Нередко, заменяют тремя составляющими:

.

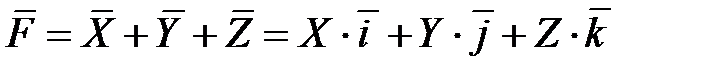Пару сил можно считать приложенной в любом месте твердого тела, момент пары есть свободный вектор, который обычно изображается из точки приложения одной из двух сил, либо – из середины плеча пары.

Внешние силы, приложенные к телу, разделяют на неизвестные силы (реакции опор, связей) и известные силы (приложенные нагрузки). В некоторых случаях известно направление реакции опоры, тогда имеем только одну неизвестную – модуль реакции опоры.

Применяется следующий прием: если в каком-либо направлении связь не препятствует бесконечно малому перемещению тела, то реакция этой связи перпендикулярна этому направлению. Система сил, приложенных к телу, называется плоской, если все неизвестные и известные силы расположены в некоторой одной плоскости 0xy.

Скалярным моментом силы относительно точки O называется произведение модуля силы и плеча силы со знаком, определяющим направление кажущегося вращения силы вокруг точки

Теорема. Если тело находится в состоянии равновесия (не движется), то система всех приложенных к нему внешних сил удовлетворяет трем алгебраическим уравнениям равновесия, а именно, равны нулю сумма моментов всех приложенных сил и суммы проекций сил на две оси координат:

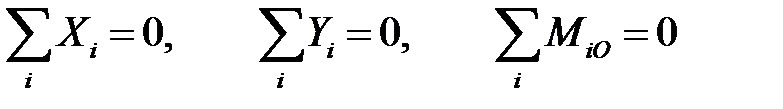
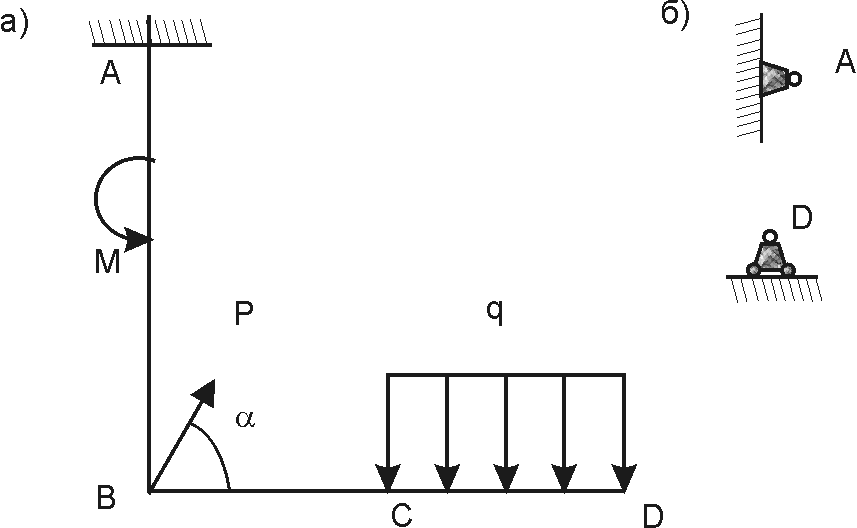
Пример 1

Рис.1 Рисунок к задаче

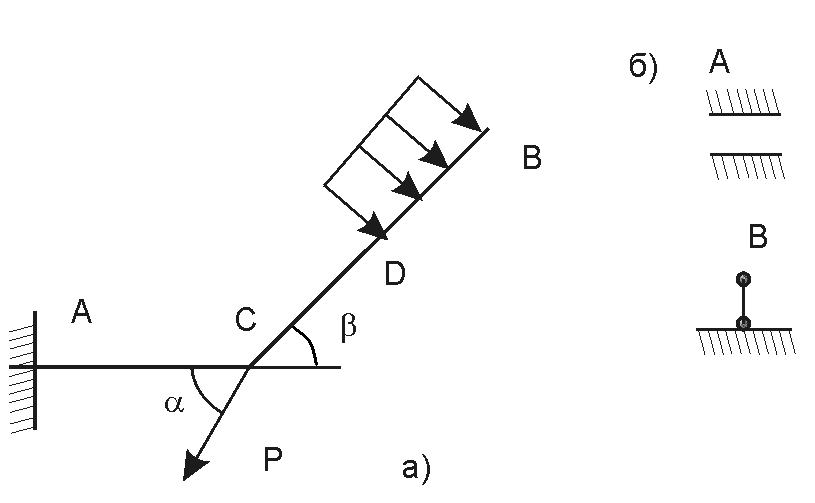
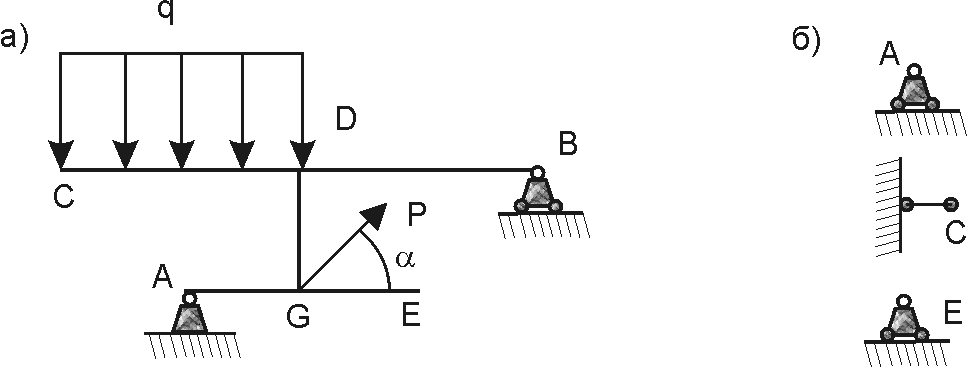
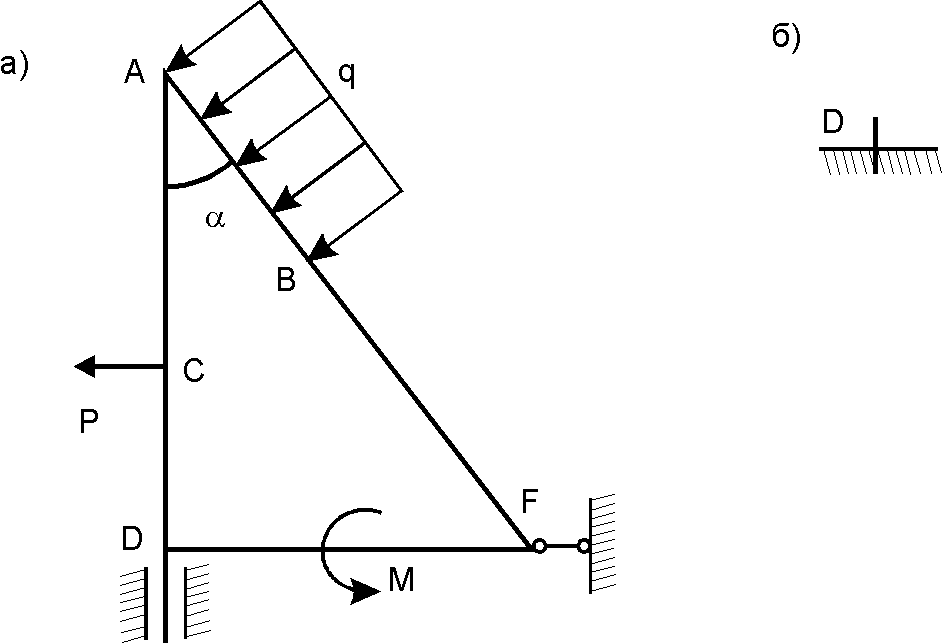
Криволинейный стержень ОАВ, опирающийся на каток и шарнир находится в состоянии равновесия. Определить реакции связей. Задан линейные размеры, и величины сосредоточенной силы и интенсивность распределенной нагрузки 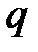, а также - момент 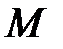пары приложенных сил (Рис.1)

Решение.

Освободим тело от связей, но сохраним действие связей и заменим нагрузку интенсивностью 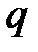на равнодействующую 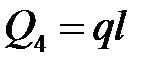, приложенную к середине участка приложения распределенной нагрузки (рис. 2). Неизвестные реакции связей 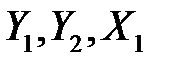направляем в положительную сторону. Продолжим пунктиром линии действия сил и покажем плечи сил относительно точки О, отметим знаком (±) направления вращения силы вместе с плечом вокруг точки О. А также перенумеруем все силы, в частности переобозначим: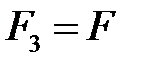

Рис.1 Реакции опор и плечи сил

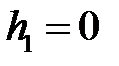плечо силы

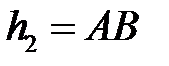– плечо силы 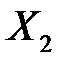, знак (-)

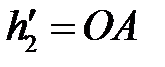– плечо , знак (+)

– плечо , знак (+), где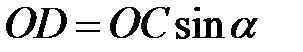

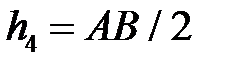– плечо , знак (-)

Составим в табличной форме два уравнения проекций и уравнение моментов относительно точки :

						M
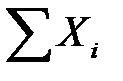
			+0	+	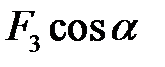+	+ 0	= 0
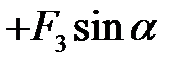
			+		+ 0	+ 0	= 0
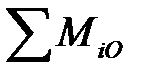
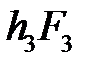
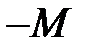
		-	+				= 0

Далее, выражая длину плеч сил через известные размеры и углы, получим систему трех линейных алгебраических уравнений относительно трех неизвестных реакций опор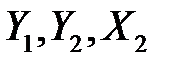

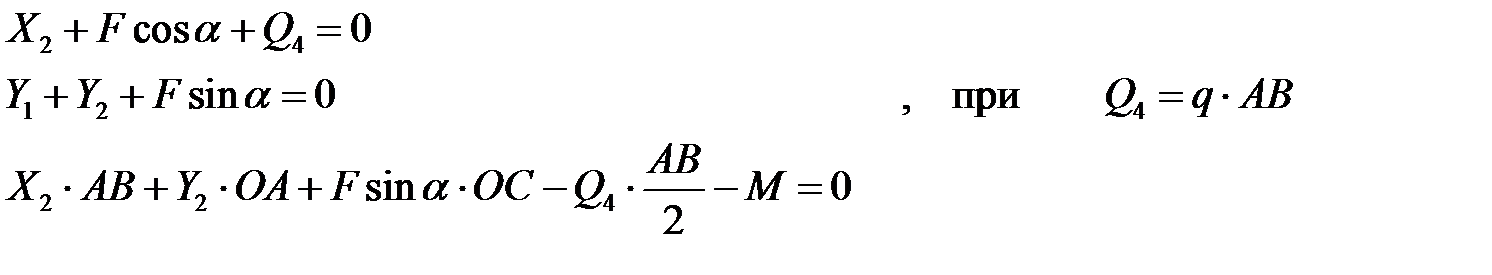
Замечание: момент любой силы можно также находить и методом разложения на составляющие, что упрощает вычисление плеч сил.

Например, имеем (рис. 3)

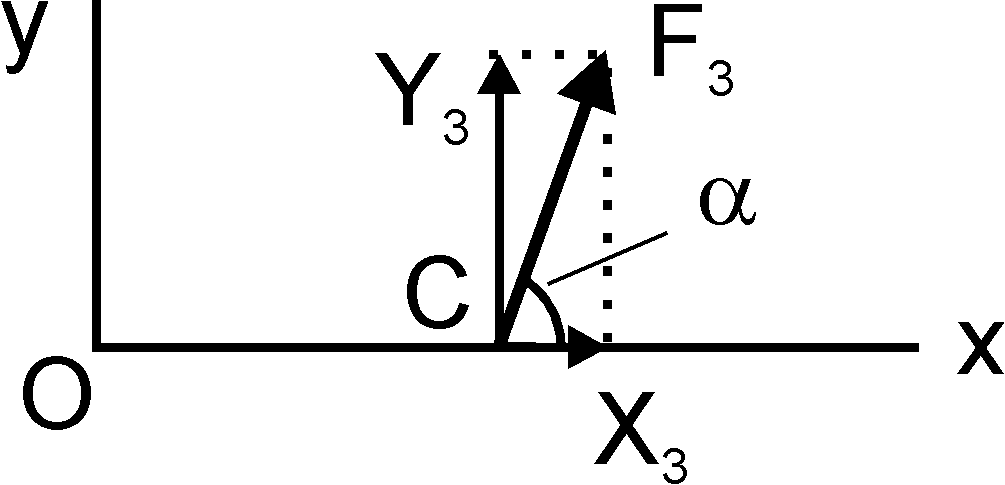
Рис. 3 Момент силы как сумма моментов ее проекций

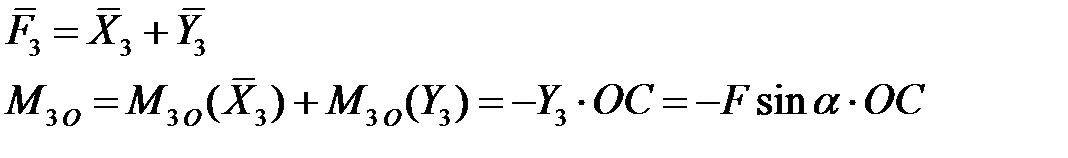
Пример 2

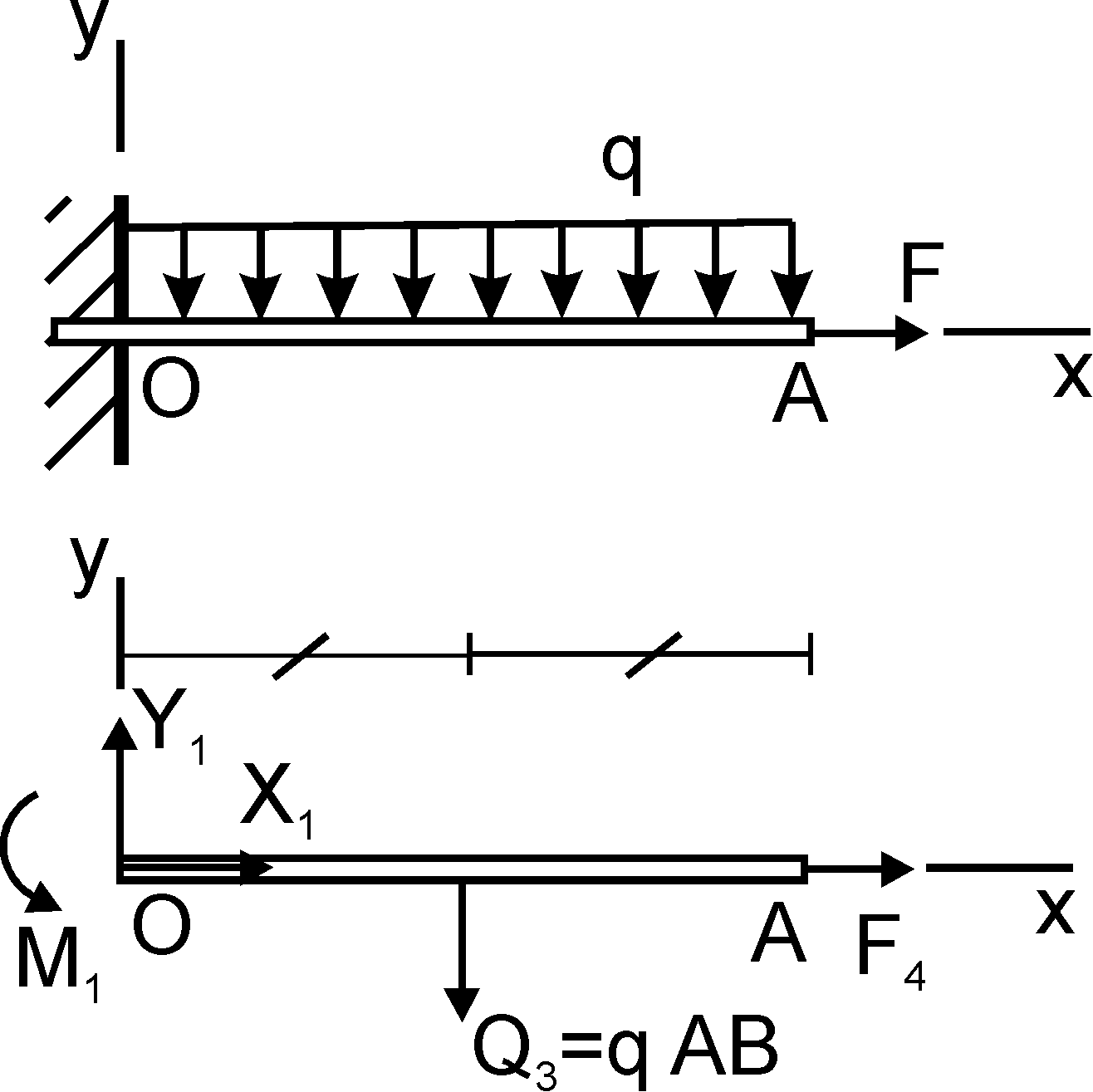
Рис. 4 Рисунок к задаче

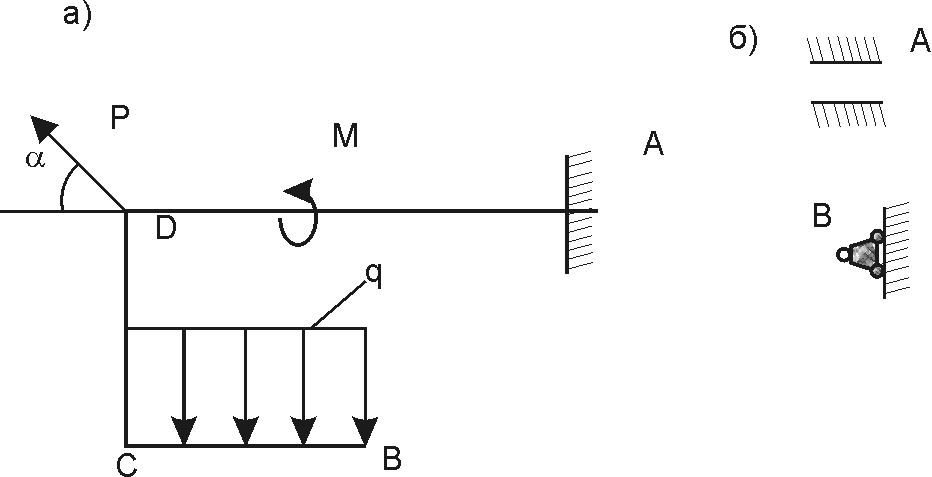
Консольная балка, закрепленная в стене. (рис. 4), нагруженная растягивающей силой F и поперечной расперделенной нагрузкой q (например - собственным весом).

Решение

В заделке возникает реакция в виде составляющих 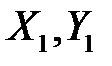, а так же - пара сил с неизвестным моментом 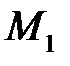удерживающие балку от вращения. Относительно О имеем плечи сил (со знаком) и уравнения равновесия в табличной форме:

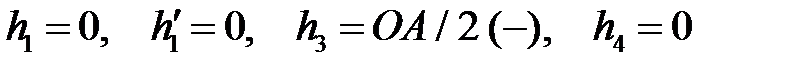
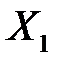
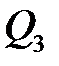
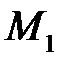
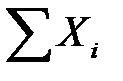
			+	+ 0	+ 0	= 0
		+0	+0		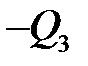+ 0	= 0
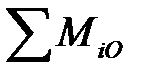
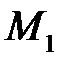
						= 0

В результате получаем систему уравнений вида

Отсюда окончательно получаем неизвестные реакции опоры:

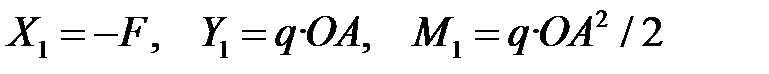
Дата добавления: 2015-06-04