Частные случаи приведения системы сил к заданному центру

Пусть в результате приведения системы сил к заданному центру 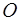получилось:

1. 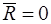, — система находится в равновесии; можно сказать, что она приводится к прямо противоположным силам.

2. 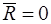, — сила отсутствует, система приводится к паре сил. Выбор полюса приведения не влияет на момент пары сил.

3. 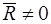, — система приводится к одной силе – равнодействующей.

4. , ,

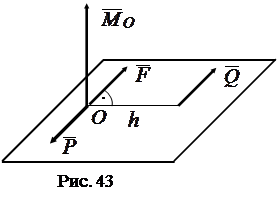
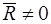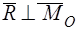
Через точку 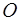проведем плоскость, перпендикулярную вектору момента 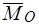(рис. 43). Приведем систему сил к силе 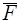и паре сил 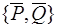, 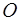– центр приведения. Сила 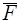лежит в проведенной плоскости, приложена в центре приведения 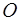и равна главному вектору: . Пара сил

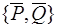
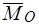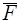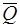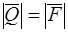с моментом также лежит в проведенной плоскости. Одну из сил пары выберем равной и прямо противоположной силе : . Другую силу пары () проводим так, чтобы момент пары был равен главному моменту системы сил, то есть .

Полученная система сил эквивалентна одной силе 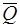, так как применяя элементарную операцию, прямо противоположные силы 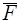и 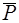можно отбросить. Система сил приводится к равнодействующей.

Общий признак существования равнодействующей

Объединяя частные случаи 2 и 4 можно установить общий признак существования равнодействующей.

Система сил приводится к равнодействующей, если главный вектор не равен нулю, а скалярное произведение главного вектора на главный момент равно нулю:

, .

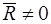Действительно, 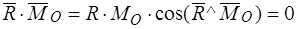(при 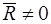), если или , то есть .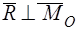

5. , , // .

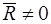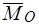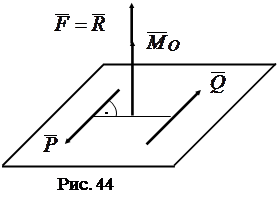Плоскость пары перпендикулярна векторам силы и момента 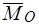. Таким образом, система эквивалентна силе 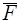и паре 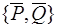, плоскость которой перпендикулярна силе (рис. 44)

Определение. Совокупность силы и пары сил, которая лежит в плоскости, перпендикулярной этой силе называют динамическим винтом или динамой.

6.

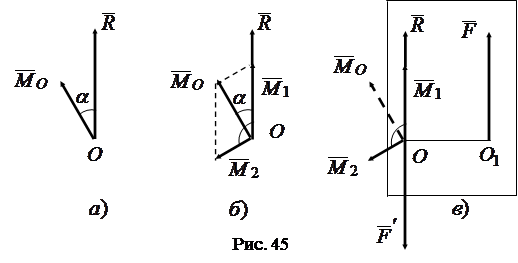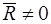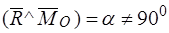, , (рис. 45а).

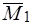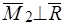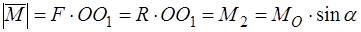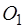Разложим вектор момента на две составляющие: // , (рис 45б). Через точку проведем плоскость, перпендикулярную вектору и построим пару такую, что , , а момент пары (рис. 45в). Таким образом, сила и пара сил с моментом эквивалентны силе , приложенной в точек , на расстоянии:

.

Следовательно, исходная система сил эквивалентна силе 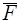и паре сил с моментом 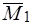, причем векторы 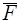и 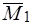параллельны. Система приводится к динаме.

Общий признак приведения системы сил к динаме

Объединяя случаи 5 и 6, получим:

Система сил эквивалентна динаме, если скалярное произведение её главного вектора на главный момент не равно нулю:

.

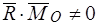Теорема Пуансо и частные случаи из нее позволяют привести заданную систему сил к простейшему виду.

Простейшие виды системы сил Условия приведения

1. Прямопротивоположные силы .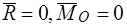

2. Пара сил .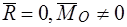

3. Одна сила (равнодействующая) .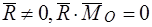

4. Динама .

Дата добавления: 2015-06-04