ЗАМЕЧАНИЕ.Система уравнений Колмогорова не является линейно независимой в силу свойств нормировки:

ЗАМЕЧАНИЕ. Для однородного марковского процесса (т.е. 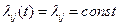), если для 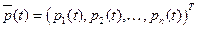существует предел при 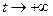, то полученный вектор называют вектором предельных состояний системы , т.е. с течением времени в системе наступает некоторый стационарный режим. Он состоит в том, что система случайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени. Каждое из состояний реализуется с некоторой постоянной вероятностью, интерпретация которой может быть связана со средним относительным временем пребывания системы в данном состоянии.

РЕКОМЕНДАЦИЯ. Уравнения Колмогорова могут составляться по следующему правилу:

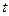производная от вероятности пребывания системы в состоянии в момент времени равна сумме произведений весов дуг, инцидентных 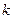- той вершине размеченного графа состояний, на вероятности состояний, к которым они направлены; при этом вес дуги берется со знаком «плюс», если дуги направлена к 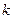- той вершине, соответствующей состоянию , и со знаком «минус» в противном случае.

ОПРЕДЕЛЕНИЕ. Марковский СП с ДС 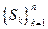называется процессом гибели-размножения, если он имеет размеченный граф состояний вида:

Поскольку для процесса гибели-размножения каждое из состояний прямой и обратной связью связано только с соседними состояниями, то система дифференциальных уравнений Колмогорова имеет сравнительно простой вид:

Для стационарного режима , поскольку 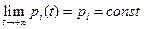, . Тогда для нахождения 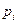, можно рассмотреть вместо системы обыкновенных дифференциальных уравнений (ОДУ) систему линейных алгебраических уравнений (СЛАУ):

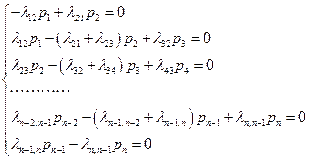
Из первого уравнения 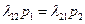, из второго и т.д., 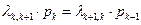, 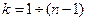. Откуда получаем ,

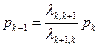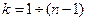
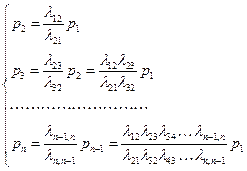
Используя свойство нормировки , получим :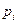

; ,

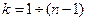
ОПРЕДЕЛЕНИЕ: Марковским СП с дискретными состояниями (МСП ДС) 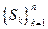называется циклическим процессом, если он имеет размеченный граф состояний вида:

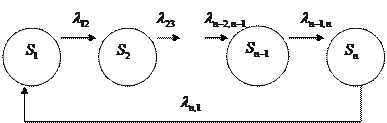
Согласно виду размеченного графа состояний однородного циклического процесса матрица 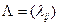плотностей вероятностей перехода имеет сравнительно простой двухдиагональный вид. Тогда однородная СЛАУ относительно вектора предельных вероятностей состояний 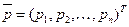имеет вид:

,

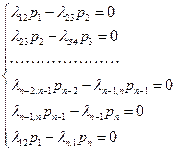из которой с учётом свойства нормировки получено:

ЗАДАЧА 1. Показать, что для однородного циклического процесса среднее время пребывания физической системы в состоянии : .

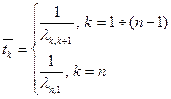
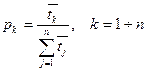Дата добавления: 2015-06-25