Момент сопротивления

Вопрос - Расчет нормальных напряжений при изгибе.

Нормальные напряжения зависят только от изгибающего момента, а касательные только от поперечной силы. Это позволяет упростить расчет нормальных напряжений для частного случая чистого изгиба, когда Q = 0.

Волокна, не изменяющие своей длины, образуют нейтральный слой. Линии пересечения нейтрального слоя с плоскостью сечения балки называется нейтральная ось.

Расчет балок на прочность проводится по максимальным нормальным напряжениям, возникающим в тех поперечных сечениях, где наибольший изгибающий момент.

Для балок из хрупких материалов составляют два условия прочности:

• для зоны растяжения:
• для зоны сжатия

Распределение нормальных нагрузок по сечению таково, что часть материала, находящегося около нейтральной оси, почти не нагружена. Наиболее целесообразно использовать двухтавровое поперечное сечение, для которого с наименьшими затратами материала можно получить наибольший момент сопротивления.

Моментом сопротивления при изгибе называется геометрическая характеристика поперечного сечения, определяющая его прочность при изгибе. Обозначается .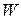

Для прямоугольника

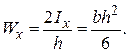
Для круга

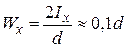
37 вопрос- Расчет на прочность при изгибе

Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают изгибающие моменты. Большей частью, в поперечных сечениях бруса наряду с изгибающими моментами возникают так же и поперечные силы, в этом случае изгиб называется поперечным.

При изгибе балки происходит искривление ее оси в плоскости действия внешней силы.

Y″= 1/ρ = M_u/EJ_z

Y - перемещение сечения балки.

1/ρ — кривизна. E — модуль упругости 1 —го рода.

J_z — экваториальный момент инерции сечения балки относительно оси z.

Величина EJ_z называется жесткостью бруса при изгибе.

Исключая кривизну из предыдущей формулы получим выражение для напряжения:

σ = M_uy/J_z

Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии

σ_max = M_uy _max/J_z

Отношение J_z/y_max называется моментом сопротивления сечения при изгибе и обозначается через W_х:

W_х = J_z/y_max

Таким образом,

σ_max = M_u/ W_х

Эта формула является основной при расчете на прочность бруса при изгибе.

Для бруса прямоугольного сечения J_z = bh³/12

Для бруса круглого сечения J_z = πD⁴/64

38 вопрос- Поперечный изгиб

Поперечный изгиб – это такой вид нагружения, при котором в поперечных сечениях бруса возникают не только изгибающие моменты Мх, но и поперечные силы Qу. Эта сила представляет собой равнодействующую элементарных распределенных сил, лежащих в плоскости сечения. В этом случае в поперечных сечениях возникают не только нормальные, но и касательные напряжения.

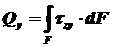
Возникновение касательных напряжений τ сопровождается появлением угловых деформаций. Поэтому, кроме основных смещений, свойственных чистому изгибу, каждая элементарная площадка сечения dF получает еще некоторые дополнительные угловые смещения, обусловленные сдвигом (рис. 10.16).

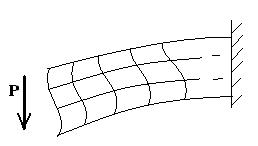
Рис. 10.16 Искривление поперечных сечений

При поперечном изгибе моменты, возникающие в левом и правом сечениях элемента, не одинаковы и отличаются на dM. Продольным горизонтальным сечением, проведенным на расстоянии у от нейтрального слоя, разделим элемент на две части и рассмотрим условия равновесия верхней части. Равнодействующая нормальных сил 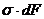в левом сечении в пределах заштрихованной площади (отсеченной части) равна

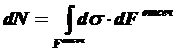
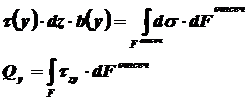
Полагая, что справедливо распределение в виде:

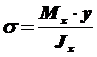, получим

,

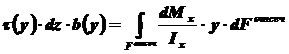
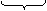
где через у обозначена текущая ордината площадки dF. Разность нормальных сил в правом и левом сечении должна уравновешиваться касательными силами, возникающими в продольном сечении элемента (рис. 10.19)

39 вопрос –Линейные и угловые перемещения при изгибе

Под действием поперечных нагрузок продольная ось искривля­ется (рис. 33.6). Если материал подчиняется закону Гука, после сня­тия нагрузок брус выпрямляется, поэтому изогнутую ось бруса назы­вают упругой линией. По форме упругой линии балки можно судить о перемещениях при изгибе.

При прямом поперечном изгибе бруса его ось, искривляясь, оста­ется в силовой плоскости. В результате деформации бруса каждое из его поперечных сечений получает вертикальное и горизонтальное перемещение, а само сечение поворачивается на некоторый угол Θ.

Деформации должны иметь упругий характер, они достаточно малы. В этом случае горизонталь­ные перемещения сечений ничтожно малы и не учитываются. Рассмат­ривают вертикальные перемещения центра тяжести сечения, называе­мые прогибами (у). Максимальные прогибы обозначают f = у_таx. Для обеспечения нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость.

Условие жесткости выражается неравенством

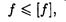
где f — максимальный расчетный прогиб балки; [f] — допускаемый прогиб. Иногда проверяется угол поворота сечения Θ < [Θ]. Допускаемый прогиб невелик: от 1/200 до 1/1000 пролета балки; допускаемый угол поворота 1*10^-3 рад.

Существует несколько методов определения перемещений сече­ний при изгибе. Один из них основан на дифференцировании урав­нения упругой линии, более рациональный способ — использование интегралов Мора. Метод Мора — универсальный способ определения линейных и угловых перемещений в любых системах.

Для облегчения расчетов на жесткость можно использовать формулы прогибов и углов поворота сечений балок для простейших случаев нагружений. Наиболее распространенные случаи нагружения и расчетные формулы приведены в таблице.

При решении используем принцип независимости действия сил. Заданный случай нагружения делится на составляющие, для кото­рых прогибы рассчитываются по известным табличным формулам, результаты расчетов суммируются.

Ограничение угла поворота вводится для обеспечения нормаль­ной работы подшипников скольжения и роликовых подшипников.

В этом случае проверяется дополнительное условие жесткости:

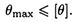
Определение линейных и угловых перемещений необходимо для расчетов на жесткость при изгибе и нахождения так называемых лишних неизвестных в статически неопределимых балках.

40 вопрос- Напряженное состояние в точке

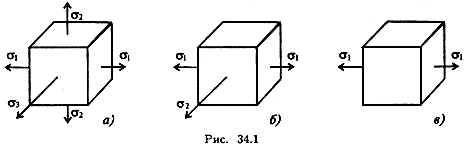
Напряженное состояние в точке характеризуется нормальными и касательными напряжениями, возникающими на всех площадках (сечениях), проходящих через данную точку. Обычно достаточно определить напряжения на трех взаимно перпендикулярных площадках, проходящих через рассматриваемую точку. Точку принято изображать в виде маленького элемента в форме параллелепипеда (рис. 34.1).

Положения теории напряженного состояния:

1. Напряженное состояние в данной точке полностью определено, если известны напряжения по любым трем взаимно перпендикулярным площадкам.

2. Среди множества площадок, которые можно провести через данную точку, есть три такие взаимно перпендикулярные площадки, на которых отсутствуют касательные напряжения, эти площадки называются главными, а нормальные напряжения, возникающие на них, называются главными напряжениями: σ₁; σ₂; σ₃ (рис. 34.1).

Одно из этих напряжений — максимально, одно — минимально. Максимальное обозначают σ₁, минимальное — σ₃.

Классификация видов напряженного состояния производится по главным напряжениям:

— если все три главных напряжения не равны нулю, то напряженное состояние называют объемным (трехосным) (рис. 34.1а);

— если одно из главных напряжений равно нулю, напряженное состояние называют плоским (двухосным) (рис. 34.15);

— если два из главных напряжений (σ₂ = 0) противоположны по знаку, напряженное состояние называют упрощенным плоским состоянием;

— если лишь одно из главных напряжений не равно нулю, на­пряженное состояние линейное (рис. 34.1 в).

41 вопрос- Сложное деформированное состояние

Сложное деформированное состояние возникает в тех случаях, когда элемент конструкции или машина подвергается одновременно нескольким простейшим деформациям.

Выше рассматривались заклепочные и шпоночные соединения, в которых одновременно возникает срез и смятие и соответственно действуют нормальные и касательные напряжения. В затянутых болтах также имеет место сложное деформирование, в них обнаруживается совместное действие растяжения от затяжки силой F и кручения от момента трения Мк. В связи с этим в болтах возникают нормальные напряжения от растяжения и касательные напряжения от кручения

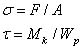
где 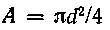— площадь сечения болта; — полярный момент сопротивления.

Нормальные напряжения распределены по сечению равномерно, а касательные достигают максимальных значений у контура болта. Очевидно, периферийные точки болта находятся в наиболее опасном состоянии, особенно в связи с наличием концентрации напряжений в нарезке.

Другим примером сложного деформирования являются валы, которые работают на изгиб и кручение. При этом в поперечном сечении вала возникают нормальные и касательные напряжения. Возникающие от изгиба нормальные напряжения достигают максимального значения в волокнах, наиболее удаленных от нейтральной оси:

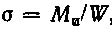
где Ми — изгибающий момент; 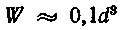— осевой момент сопротивления сечения.

Максимальные касательные напряжения при кручении возникают в точках контура поперечного сечения

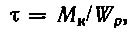
где Wp = 0,2d^3 — полярный момент сопротивления.

Так как Wp = 2W, то

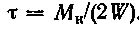
Следовательно, в наиболее напряженных точках вала при совместном действии изгиба,и кручения возникают нормальные и касательные напряжения. Встает вопрос, какое же из этих напряжений или какая их комбинация определяют прочность вала. Ответ на этот вопрос дают так называемые теории (или гипотезы) прочности.

42 вопрос- Устойчивость сжатых стержней

Деформированное состояние центрально-сжатого стержня (рис. 8.1, а) может быть устойчивым или неустойчивым. Если вывести стержень из первоначального состояния малой дополнительной горизонтальной силой Р, то он окажется искривлённым (рис. 8.1, б). После удаления силы Р стержень либо возвращается в первоначальное прямолинейное состояние (рис. 8.1, в), либо остаётся искривлённым (рис. 8.1, г). Первый случай соответствует устойчивому деформированному состоянию стержня, второй случай – неустойчивому деформированному состоянию.

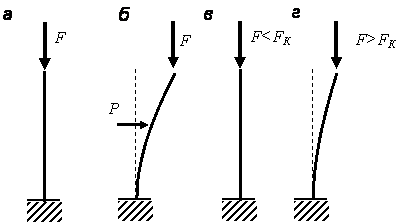
Рис. 8.1. Состояния сжатого стержня: а – исходное; б – стержень с дополнительной поперечной нагруз­кой Р; в – прямолинейный стержень после удаления силы Р; г – криволинейный стержень после удале­ния силы Р

Между устойчивым и неустойчивым состояниями теоретически существует промежуточное, называемое критическим состоянием, при котором стержень после удаления силы Р может остаться в равновесии как в прямолинейном состоянии, так и в криволинейном. При заданных размерах стержня вид его деформированного состояния зависит от величины сжимающей силы.

Наибольшая величина сжимающей силы, при которой деформированное состояние стержня ещё устойчивое, называется критической силой, обозначаемой F_К (рис. 8.1)

Превышение величины критической силы приводит к потере устойчивости, при которой малые поперечные нагрузки приводят к большим изгибным перемещениям стержня и возможному его разрушению.

Отношение критической силы к площади поперечного сечения стержня называют критическим напряжением .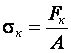

В том случае, когда критические напряжения не превышают предела пропорциональности материала 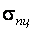, потеря устойчивости начинается при упругом деформировании стержня и критическую силу вычисляют по формуле Эйлера

,

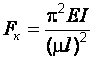где 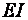_– изгибная жёсткость; 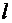– геометрическая длина стержня; 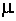– коэффициент приведения длины стержня, зависящий от способов закрепления концов стержня (табл. 8.1). Произведение 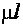называется приведённой длиной стержня.

Для сжатых стержней вводится безразмерная характеристика, называемая гибкостью 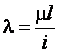, где 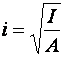– радиус инерции поперечного сечения.

Формула Эйлера справедлива при условии .

43 вопрос- Расчет на устойчивость сжатых стержней.Критическая сила.

Для сжатых стержней должно выполняться условие устойчивости 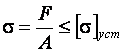, в котором допускаемые напряжения на устойчивость получаются делением критических напряжений на коэффициент запаса устойчивости 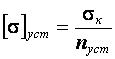. Принято выражать величину через величину основных допускаемых напряжений при расчетах на прочность 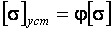, где множитель 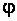называется коэффициентом продольного изгиба. Этот коэффициент зависит от гибкости и материала стержня, его величина меньше единицы и находится из справочных таблиц.

Для практических расчётов условие устойчивости записывают в виде

.

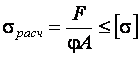Наибольшая величина сжимающей силы, при которой деформированное состояние стержня ещё устойчивое, называется критической силой, обозначаемой F_К (рис. 8.1)

Превышение величины критической силы приводит к потере устойчивости, при которой малые поперечные нагрузки приводят к большим изгибным перемещениям стержня и возможному его разрушению.

Отношение критической силы к площади поперечного сечения стержня называют критическим напряжением .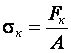

44 вопрос – Критическое напряжение при расчете на устойчивость сжатых стержней

Превышение величины критической силы приводит к потере устойчивости, при которой малые поперечные нагрузки приводят к большим изгибным перемещениям стержня и возможному его разрушению.

Отношение критической силы к площади поперечного сечения стержня называют критическим напряжением .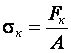

В том случае, когда критические напряжения не превышают предела пропорциональности материала 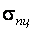, потеря устойчивости начинается при упругом деформировании стержня и критическую силу вычисляют по формуле Эйлера

,

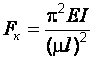где 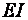_– изгибная жёсткость; 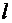– геометрическая длина стержня; 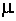– коэффициент приведения длины стержня, зависящий от способов закрепления концов стержня (табл. 8.1). Произведение 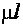называется приведённой длиной стержня.

45 вопрос- Сопротивление усталости.Понятие о цикле.

Сопротивление усталости материала определяется по результатам испытаний на усталость гладких образцов с плавным утонением в зоне предполагаемого разрушения. Результаты испытаний на усталость образцов разного размера концентрацией напряжений при наложении постоянно действующей - статической нагрузки в условиях нагрева и с различной частотой нагружения позволяют построить зависимости пределов выносливости от конструктивных и эксплуатационных факторов и использовать их для расчетной оценки характеристик усталости деталей.

Для оценкисопротивления усталости материалов, предназначенных для производства энергетических установок, химического и другого оборудования, нами [80] разработана методика и создано оборудование для испытания материалов на усталость при периодическом смачивании, нагретых до повышенных температур образцов, брызгами коррозионной среды. [ 7 ]

Совокупность термодинамических процессов, в результате которых рабочее тело возвращается в исходное состояние, называется термодинамическим циклом, или круговым процессом.

46 вопрос- Факторы влияющие на сопротивление усталости

Сопротивление усталости материалов в общем случае зависит от трех групп факторов, связанных, во-первых, с характером напряженного состояния детали или образца, во-вторых, со свойствами материала, и, в-третьих, с воздействием окружающей среды. Причины остановки роста усталостной трещины целесообразно рассматривать с учетом именно этих групп факторов.

Дата добавления: 2015-06-25