Применение теории игр к строительству противолавинных сооружений

Второй пример связан со строительством противолавинных сооружений.

Использование горной территории в рекреационных целях всегда связано с проблемой защиты от лавин и селей: зданий, канатных дорог, используемых для катания склонов, а также проживающих в этих районах жителей и горнолыжников, катающихся по данным склонам. В целях безопасности часто требуется строительство противолавинных сооружений, а для этого нужны значительные материальные затраты. Именно поэтому необходимо создание карт лавинной опасности территории, связанной с рекреационной деятельностью. Карты лавинной опасности помогают прояснить в целом лавинную ситуацию района. Одной из задач для составления карт является оценка объема снега, который может быть потенциально вовлечен в движение и, в результате, принести материальный ущерб.

Предположим теперь, что карты лавинной опасности имеются и на них отмечены участки, подвергающиеся лавинной опасности один раз во много лет. Проанализируем данную ситуацию. Если организация, которая контролирует данную ситуацию, располагает большим количеством материальных средств, то никакой научной задачи не возникает. Можно построить (с избытком) на всех склонах противолавинные сооружения, создать рекламу о безопасности катания на данных склонах в виду наличия противолавинных сооружений и получать соответствующую ситуации выгоду. Проблема возникает (а это более реальная жизненная ситуация), когда имеется ограниченное количество материальных средств. Стоит ли создавать на всех участках противолавинные сооружения при ограниченном количестве материальных средств? Какие выбрать участки? Такая задача может быть отнесена к области конфликтных ситуаций, и аппарат теории игр может помочь наилучшим образом распределить имеющиеся материальные средства для создания противолавинных сооружений.

Проанализируем данную задачу. Пусть на территории, подвергающейся сходу лавин, имеются лавиноопасные склоны, по которым с определенными частотами движутся лавины (или сели, или то и другое вместе) в разное время в течение года. Сход лавин приносит определенный материальный ущерб и порой угрожает здоровью и даже создает угрозу жизни людей. Требуется создать противолавинные сооружения, с учетом того, что количество средств, отпущенных на создание этих противолавинных сооружений, ограничено суммой М. Как наиболее оптимально распределить эти средства? Данная задача относится к области конфликтных ситуаций, и конечный результат зависит от конкретных действий каждой из сторон. В одном случае при этом подразумеваются действия человека, в другом - природы.

Рассматривая строительство противолавинных сооружений, мы имеем дело с игрой m* n. Это означает, что природа имеет m стратегий (лавиноопасных склонов), а человек имеет n стратегий (в частности, он может построить на склоне противолавинное (одно или несколько) сооружение). Данная игра содержит случайные ходы, так как мы не знаем точно время, когда сойдет лавина.

Для решения задачи в области смешанных стратегий введем 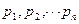- относительные частоты применения стратегий и запишем следующую систему уравнений:

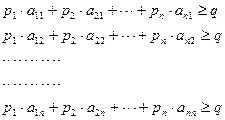(2.26)

Разделим левые части уравнения (2.26) нa q и введем обозначения:

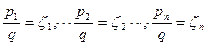(2.27)

Перепишем уравнение (2.27) в следующем виде:

(2.28)

Так как желание человека заключается в увеличении выигрыша, следовательно:

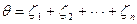должна быть минимальной. Для решения такого рода задачи разработан математический аппарат линейного программирования. Решение уравнений (2.28) дает возможность вычислять цену игры q.

Перераспределяя различными способами сумму М, отпущенную на строительство противолавинных сооружений, человек изменяет коэффициенты матрицы.

Вычисляя в каждом конкретном случае цену игры q, можно найти оптимальный вариант, который дает возможность распределить средства таким образом, чтобы выигрыш со стороны человека был максимален.

Рассмотрим в качестве иллюстрирующего примера два лавиноопасных склона, по которым спускаются лавины мощностями 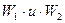. Будем считать, что ущерб, производимый лавиной, прямо пропорционален ее мощности и равен: 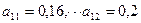. (Коэффициенты 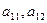получены путем перемножения мощностей лавин 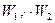на вероятности их схода 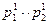. Для расчета использовались следующие значения: , ).

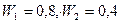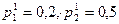Предположим, что суммы противолавинных средств М, имеющейся в наличии, хватает ровно для того, чтобы создать противолавинные сооружения, преграждающие путь лавине мощностью 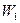. Допустим, что 50% средств М достаточно для полной защиты от лавины мощностью 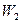. Рассмотрим три варианта (три стратегии) со стороны человека. При первой стратегии (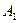) все средства М тратятся на преграждение пути лавины мощностью 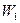, при этом вторая лавина может двигаться беспрепятственно. Суть второй стратегии (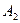) в следующем: средства делятся пополам для создания противолавинных сооружений первой и второй лавин. При этом вторая лавина будет полностью закрыта. Согласно третьей стратегии (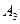) все средства тратятся на создание сооружения для второй лавины. Матрица игры будет иметь следующий вид:

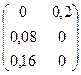(2.29)

Так как каждый элемент стратегии 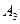больше или равен элементу стратегии 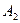, то стратегия 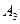заведомо невыгодная, и ее можно вычеркнуть. Решая систему уравнений, содержащую две стратегии человека ():

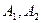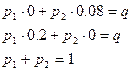(2.30)

найдем

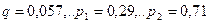
Данное решение означает следующее: для получения выигрыша 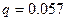надо в 29 % пользоваться стратегией 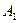, а в 71 % стратегией .

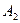Конечно, сход лавин – явление вероятностное, тем не менее, в данном случае вторая стратегия явно предпочтительнее.

Дата добавления: 2015-06-26