Динамика. Основной закон динамики ( 2-ой закон (Ньютона)):

Основной закон динамики (2-ой закон (Ньютона)): 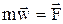. Дифференциальные уравнения движения материальной точки: ,

; . –

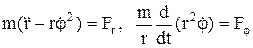– дифференциальное уравнение прямолинейного движения точки, его общее решение:

x=f(t,C₁,C₂), начальные условия: t=0, x=x₀, =V_x=V₀.

Свободные колебания ; c/m=k², 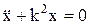; x= C₁coskt + C₂sinkt,

= – kC₁sinkt + kC₂coskt, С₁= х₀, С₂= /k, т.е. x= х₀coskt + ( /k)sinkt.

С₁=Аsinb, C₂=Acosb, x=Asin(kt+b) – гармонические колебания, А= 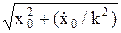амплитуда, tgb=kx₀/ , b – начальная фаза свободных колебаний; – собственная частота колебаний; период Т=2p/k. Статическое отклонение d_ст=Р/с. Т=2p .

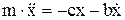Затухающие колебания R_x= – b сила сопротивления, , b/m=2n, 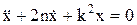, характеристическое уравнение: z² + 2nz + k²= 0, его корни:

z_1,2= . а) n<k ,

x=Ae^-ntsin(kt+b). , 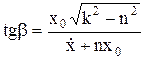; частота затухающих колебаний: k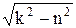^*= ; период: 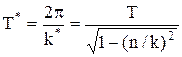. – декремент колебаний; –nT^*/2 логарифмический декремент; "n" – коэффициент затухания.

Б) Апериодическое движение n ³ k. При n > k: , обозначая С₁=(В₁+В₂)/2, С₂=(В₁-В₂)/2, . При n = k: , ,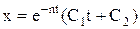

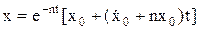Вынужденные колебания: возмущающая сила: Q = Hsin(pt+d), р – частота возмущающей силы, d – начальная фаза. 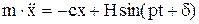, h=Н/m, .

х = х^*+х^**. х^*= C₁coskt + C₂sinkt, х^**= Asin(рt+d).

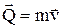– количество движения материальной точки, 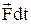– элементарный импульс силы. – теорема об изменении количества движ. матер. точки в дифф. форме или . 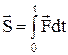– импульс силы за [0,t]. В проекциях на оси координат: 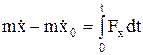и т.д. 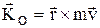- момент количества движения матер.

точки относительно центра О. Теорема об изменении момента количества движения матер. точки. . Если М_О= 0, Þ 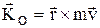=const. 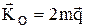=const,

где – секторная скорость. Элементарная работа dA = F_tds, F_t – проекция силы на касательную к траектории, или dA = Fdscosa. dA= – скалярное произведение; dA= F_xdx+F_ydy+F_zdz. Работа силы на любом конечном перемещении М₀М₁:

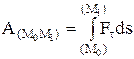. Если F=const, то = F×s×cosa. , .

Работа силы тяжести: 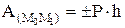. A>0, если М₀ выше М₁.

Работа силы упругости: .

Работа силы трения: 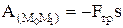, F_тр=fN. Сила притяжения (тяготения): , k=gR². Работа силы тяготения: .

Мощность 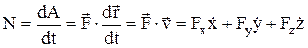. Если N=const, то N=A/t.

Теорема об изменении кинетической энергии точки. В дифференциальной форме: . – кинетическая энергия материальной точки. В конечном виде: . 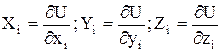, U=U(x₁,y₁,z₁,x₂,y₂,z₂,…x_n,y_n,z_n) – силовой функцией. Элементарная работа сил поля: dА=ådА_i= dU. Работа сил на конечном перемещении . Потенциальная энергия – П равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. А_1,2= П₁– П₂. Потенц. энергия поля силы тяжести: П= mgz. Потенциальная энергия поля центральных сил. Центральная сила – 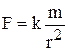, 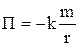. Гравитационная сила , , f = 6,67×10^-11м³/(кгс²) – постоянная тяготения.

Первая космическая скорость v₁= 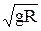» 7,9 км/с, R = 6,37×10⁶м – радиус Земли; вторая космическая скорость: v₁₁= » 11,2 км/с.

Потенциальная энергия восстанавливающей силы пружин: , l – модуль приращения длины пружины. Работа восстанавливающей силы пружины: .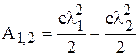

Дата добавления: 2015-06-04