Смешанное произведение векторов и его свойства. 1 страница

Векторное произведение 2х векторов.

Скалярное произведение векторов и его свойства.

-(“skala”-шкала) 2х векторов а и в наз. число, равное произведению длин этих векторов на cos угла между ними. (а, в)- скалярное произведение. а * в =| а |*| в |*cosj, j=p/2, cosp/2=0, a^b=> ab =0. Равенство “0” скаляргного произведения необходимое и достаточное условие их перпендикулярности (ортогональности).

левая ----- правая

Тройка векторов а, в, с наз. правоориентированной (правой), если с конца 3го вектора с кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки - левая. Векторным произведением 2х векторов а и в наз. такой вектор с, который удовлетворяет условиям: 1. | c |=| a |*| b |*sinj. 2. c ^ a и c ^ b. 3. тройка а, в, с -правая.

Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a * b * c =[ a * b ]* c = a *[ b * c ], где

a ={a_x,a_y,a_z}

b ={b_x,b_y,b_z}

c ={c_x,c_y,c_z}

Св-ва:
1. При перестановке 2х сомножителей:

a * b * c =- b * c * a

2. не меняется при перестановке циклических сомножителей:

a * b * c = c * a * b = b * c * a

3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a * b * c =0

б)если некомпланарные вектора a, b, c привести к 1 началу, то | a * b * c |=Vпараллепипеда, построенного на этих векторах

если a * b * ca, b, c - правая

если a * b * c <0, то тройка a, b, c – левая

Тема «Оптимизационные методы и модели»:

Общая задача линейного программирования и составление моделей задач математического программирования. Графический метод решения задачи линейного программирования. Симплексный метод решения задачи линейного программирования. Двойственные задачи линейного программирования

Методы линейного программирования в математике известны под названием общей задачи линейного программирования. Аналитическая формулировка общей задачи линейного программирования. Общая задача линейного программирования формулируется следующим образом:
Найти решение {Х₁,Х₂,….Х_n}, позволяющее максимизировать или минимизировать целевую функцию
F = C₁X₁+C₂X₂+…+ C_nX_n
при условиях

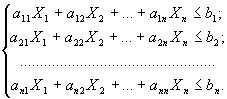
Х₁≥0; Х₂≥0; …; Х_n≥0.
Это развернутая запись общей задачи линейного программирования. Сокращенная запись этой модели имеет вид:
Найти решение {X_j}, позволяющее максимизировать (минимизировать) функцию

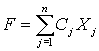
при условиях
, i = 1,2,…,n;
X_j ≥ 0, j = 1,2,…,n.
Вышеприведенные записи общей задачи линейного программирования называют аналитической формой записи.
Любое решение, удовлетворяющее условиям, называется допустимым решением. Допустимое решение систем неравенств, удовлетворяющее целевой функции, называется оптимальным решением. Такое решение единственно при заданных условиях.
Матричная форма записи общей задачи линейного программирования

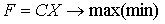
при ограничениях AX≤B
X≥0
где С = (с₁, с₂,…, с_n);

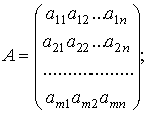
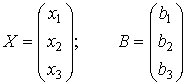
где С – матрица-строка
А – матрица системы
Х – матрица-столбец переменных
В – матрица-столбец свободных членов
2 Многокритериальная оптимизация. Методы сведения многокритериальной задачи к однокритериальной.
Многокритериальная оптимизация представляет собой минимизацию некого вектора целей F(x), на которой могут быть наложены дополнительные ограничения или предельные значения
Отметим, что поскольку F(x) является неким вектором, то любые компоненты F(x) являюся конкурирующими и отсутсвует некое единое решение поставленной задачи. Взамен этого, для описания характеристик целей вводится концепция множества точек неулучшаемых решений (так называемая оптимальность по Парето).Неухудшаемое решение есть такое решение, в котором улучшение в одной из целей приводит к некому ослаблению другой. Для более точной формулировки данной концепции рассмотрим некую область допустимых решений в параметрическом пространстве , которое удовлетворяет всем принятым ограничениям.
Отсюда возможно определить соответствующую область допустимых решений для пространства целевых функций .
, где
при условии
Определение. Точка является неулучшаемым решением, если для некоторой окрестности 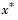нет некого 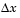такого, что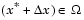

Стратегия взвешенных сумм
Данная стратегия взвешенных сумм преобразует многокритериальную задачу минимизации вектора 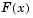в некую скалярную задачу путем построения неких взвешенных сумм для всех выбранных объектов.

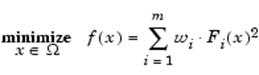
Далее уже к данной задаче оптимизации уже может быть применен стандартный алгоритм оптимизации без наличия ограничений. В этом случае рассматриваются взвешенные коэффициенты для каждой из выбранных целей. Взвешенные коэффициенты необязательно должны напрямую соответствовать относительной значимости соответствующей цели или принимать во внимание взаимовлияние между конкретно выбранными целями. Более того, границы неулучшаемых решений могут быть и не достигнуты, так что определенные решения являются по существу недостижимыми.
Метод -ограничений
Некий определенный способ, который отчасти позволяет преодолеть проблему выпуклости метода взвешенных сумм, есть метод -ограничений. В этом случае осуществляется минимизация основной цели 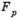и при представлении остальных целей в форме ограничений типа неравенств.

при выполнении условия

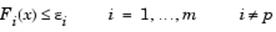
Подобный подход позволяет определить некое количество неулучшаемых решений для случая вогнутой границы, что, по существу, является недоступным в методе взвешенных сумм, например, в точке искомого решения 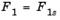и . Однако проблемой данного метода является подходящий выбор , который мог бы гарантировать допустимость некого решения.
Метод достижения цели
Описанный далее метод представляет собой метод достижения цели Гембики. Данный метод включает в себя выражение для множества намерений разработчика , которое связано с множеством целей . Такая формулировка задачи допускает, что цели могут быть или недо- или передостижимыми, и что дает разработчику возможность относительно точно выразить исходные намерения. Относительная степень недо- или передостижимости поставленных намерений контролируется посредством вектора взвешенных коэффициентов и может быть представлена как стандартная задача оптимизации с помощью следующей формулировки

При условии, что

Член 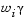вносит в данную задачу элемент ослабления, что, иначе говоря, обозначает жесткость заданного намерения. Весовой вектор w дает исследователю возможность достаточно точно выразить меру взаимосвязи между двумя целями. Например, установка весового вектора w как равного исходному намерению указывает на то, что достигнут тот же самый процент недо- или передостижимости цели . Посредством установки в ноль отдельного весового коэффициента (т.е. 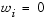) можно внести жесткие ограничения в поставленную задачу. Метод достижения цели обеспечивает подходящую интуитивную интерпретацию поставленной исследовательской задачи и которая, в свою очередь, является вполне разрешимой с помощью стандартных процедур оптимизации.
3 Гладкая оптимизация.
Метод множителей Лагранжа позволяет отыскивать максимум или минимум функции при ограничениях-равенствах. Основная идея метода состоит в переходе от задачи на условный экстремум к задаче отыскания безусловного экстремума некоторой построенной функции Лагранжа. Пусть задана задача НП при ограничениях-равенствах вида
минимизировать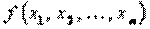
при ограничениях

Предположим, что все функции – дифференцируемы. Введем набор переменных (число которых равняется числу ограничений), которые называются множителями Лагранжа, и составим функцию Лагранжа такого вида:

Справедливо такое утверждение для того чтобы вектор 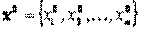являлся решением задачи при ограничениях необходимо, чтобы существовал такой вектор , что пара векторов удовлетворяла бы системе уравнений


множителей Лагранжа, который состоит из следующих шагов.
Составляют функцию Лагранжа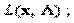
Находят частные производные
Решают систему уравнений

и отыскивают точки , удовлетворяющие системе.
Найденные точки 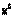дальше исследуют на максимум (или минимум).
Седловая точка и задача нелинейного программирования
Рассмотрим функцию Лагранжа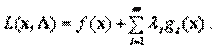
Определение Пара векторов 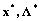называется седловой точкой функции Лагранжа , если при всех выполняется условие

Неравенство называют неравенством для седловой точки. Очевидно, что в седловой точке выполняется условие

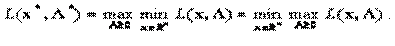
Между понятием седловой точки функции Лагранжа и решением задачи НП существует взаимосвязь, которая устанавливается в следующей теореме.
Теорема. Пусть 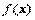и все выпуклы и функции 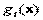удовлетворяют условию регулярности Слейтера. Вектор 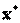является решением задачи НП тогда и только тогда, когда существует такой вектор , что

Теорема Куна-Таккера. Пусть функции , имеют непрерывные частные производные на некотором открытом множестве 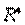, содержащем точку 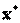. Если является точкой минимума функции 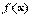при ограничениях , удовлетворяющих условию регулярности в виде линейной независимости векторов , то существуют такие неотрицательные множители Лагранжа 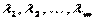, что


Определим функцию Лагранжа следующим образом:

Тогда теорему Куна-Таккера можно записать в виде



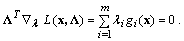
Заметим, что множители Лагранжа в задаче НП с ограничениями-равенствами являются знаконеопределенными, тогда как в теореме Куна-Таккера они должны быть положительными.
Каждой задаче линейного программирования соответствует двойственная задача. Двойственная задача по отношению к исходной задаче строится по следующим правилам:
· Если исходная задача ставится на максимум, то двойственная ставится на минимум и наоборот.
· Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи. Правые части ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи.
· Если A-матрица коэффициентов исходной задачи, то транспонированная матрица T A будет матрицей коэффициентов двойственной задачи.
· В задаче на максимум все ограничения имеют знак ≤ (=), а в задаче на минимум все ограничения имеют знак ≥.
· Число переменных в двойственной задаче равно числу ограничений в исходной задаче. Каждому ограничению исходной задачи соответствует переменная двойственной задачи. Если ограничение исходной задач имеет знак (≥), то соответствующая переменная двойственной задачи неотрицательна. Если ограничение имеет знак (=), то соответствующая переменная двойственной задачи может принимать положительные и отрицательные значения и наоборот.
4 Выпуклая оптимизация. Условие выпуклости
Основная задача выпуклого программирования
Пусть задано выпуклое и замкнутое множество . Рассмотрим множество
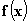={ }, =(,…, ), Î .
где 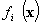(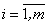) — вогнутые (выпуклые вверх) непрерывные на скалярные функции. В теории математического программирования каждый элемент Î принято называть допустимым планом, а само множество — множеством допустимых планов.
Формальная постановка задачи выпуклого программирования
Задачу
,
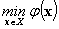где выпукла, а определяется вышеприведенными условиями, называется основной задачей выпуклого программирования.
REF _Ref433730605 \r \* MERGEFORMAT 0означает, что ставится задача:
Если существует минимальное значение функции на множестве , то среди всех допустимых планов найти оптимальный план 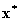, для которого
= =
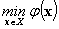
при этом число называют значением задачи.
Если оптимального плана не существует, то требуется
· либо найти значение задачи как точную нижнюю грань значений функции на множестве :
=
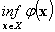
· либо убедиться, что неограничена снизу на множестве ;
· либо убедиться в том, что множество допустимых планов пусто.
Для решения предложенной оптимизационной задачи следует выполнить следующие действия:
· Определить множество .
· Определить вектор-функцию 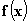=(,…, ) и вектор Î .
· Определить множество допустимых планов ={ }.
· Привести задачу к стандартной форме основной задачи выпуклого программирования и определить оптимизируемую функцию .
· Проверить, является ли полученная оптимизационная задача ЗВП, для этого
· проверить на выпуклость множество ;
· проверить на выпуклость функцию .
В случае успеха п. REF _Ref435679505 \r \* MERGEFORMAT ·
· Построить функцию Лагранжа полученной ЗВП.
· С помощью дифференциальных условий Куна-Таккера найти седловые точки построенной функции Лагранжа.
В случае неудачи п. REF _Ref435679505 \r \* MERGEFORMAT ·попытаться найти другие методы решения задачи.
Методы субградиентной оптимизации. Эти итеративные процедуры формируют последовательность векторов {l^k}.
Фундаментальный теоретический результат заключается в том, что
.
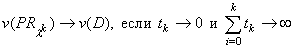Размер шага на практике обычно выбирают, следуя,

где q ^k — скаляр, 0 < q ^k 2 и z* — верхняя граница для n(D). Обычно z* получают эвристикой для P. В методе ветвей и границ z* — текущий рекорд. Последовательность q ^k, как правило, начинается с q ⁰=2 и затем q ^k делится пополам, через фиксированное число итераций, зависящее от размерности задачи.

Тема «Эконометрические модели»:

Корреляция, вычисление коэффициентов корреляции. Линейная модель парной регрессии. Модель множественной регрессии. Анализ временных радов экономических процессов

Эконометрика как научная дисциплина расположена на стыке экономики, статистики и математикиОбычно в качестве ее основных задач выделяют обнаружение и анализ статистических закономерностей в экономике, построение на базе выявленных эмпирических экономических зависимостей эконометрических моделей

В качестве самостоятельной отрасли знания эконометрика оформилась в начале 30-х годов XX векаТермины «эконометрика» и «эконометрия» стали общеупотребительными благодаря норвежскому экономисту РФришуСогласно РФришу, эконометрика объединяет «как чистую экономическую теорию, так и статистическую проверку законов чистой экономической теории»Более конкретно: «сущность эконометрики заключается во взаимном переплетении количественной экономической теории и статистических оценок».[1] Отсюда следует, что к числу эконометрических относятся отнюдь не все модели, а лишь такие, которые позволяют проводить статистические операцииСуществует не мало моделей и развернутых на их основе «количественных теорий», являющихся экономико-математическими, но вовсе не эконометрическимиПоскольку за каждой переменной эконометрической модели стоит определенный статистический индикатор, с той или иной точностью измеряющий какую-то сторону хозяйственного механизма, расчеты на базе этой модели, как правило, имеют достаточно высокую практическую ценностьОни могут быть использованы при выработке экономической политики государства, рыночной стратегии фирмы и решении других конкретных задач.

Методологическая особенность эконометрики заключается в применении общих гипотез о статистических свойствах экономических параметров и ошибок при их измеренииПолученные при этом результаты могут оказаться нетождественными тому содержанию, которое вкладывается в реальный объектПоэтому важная задача эконометрики – создание как более универсальных, так и специальных методов для обнаружения наиболее устойчивых характеристик в поведении реальных экономических показателейЭконометрика разрабатывает методы «подгонки» формальной модели с целью наилучшего имитирования ею поведения моделируемого объекта на основе гипотезы о том, что отклонение модельных параметров от реально наблюдаемых случайны и вероятностные характеристики их известны.

Главным инструментом эконометрики служит эконометрическая модель – модель факторного анализа, параметры которой оцениваются средствами математической статистики. Такая модель выступает в качестве средства анализа и прогнозирования конкретных экономических процессов на основе реальной статистической информации.

Можно выделить три основных класса эконометрических моделей:

1) Модели временных рядовК этому классу относятся модели:

– Тренда:

Y(t) = T(t) +?t,

где T(t) – временной тренд заданного вида (например, линейный T(t) = а + bt),?t – стохастическая (случайная) компонента;

– Сезонности:

Y(t) = S(t) +?t,

где S(t) – периодическая (сезонная) компонента,?t - стохастическая (случайная) компонента;

– Тренда и сезонности:

Y(t) = T(t) + S(t) +?t, аддитивная («дополняющая»),

Y(t) = T(t) S(t) +?t, мультипликативная («множительная»),

где T(t) – временной тренд заданного вида, S(t) – периодическая (сезонная) компонента,?t – стохастическая (случайная) компонента;

К моделям временных рядов относится множество более сложных моделей, таких, как модели адаптивного прогноза, модели авторегрессии и скользящего среднего (ARIMA) и дрих общей чертой является объяснение поведения показателя во времени, исходя только из его предыдущих значенийТакие модели могут применяться, например, для прогнозирования объемов производства, объемов продаж, краткосрочного прогноза процентных ставок и тп.

2) Регрессионные модели с одним уравнениемВ таких моделях зависимая (объясняемая) переменная Y представляется в виде функции f (x,?) = f (x1, …, хn,?1, …,?m), где x1, …, хn - независимые (объясняющие) переменные,?1, …,?m – параметрыВ зависимости от вида функции f (x,?) модели делятся на линейные и нелинейныеНапример, можно исследовать среднедушевой уровень потребления населения как функцию от уровня доходов населения и численности населения, или зависимость заработной платы от возраста, пола, уровня образования, стажа работы и т.д.

Тема «Информационные технологии документального обеспечения управленческой деятельности»:

Документ, его роль в организации управления. Цели и методы стандартизации и унификации управленческой документации. Документооборот и его организация. Контроль использования управленческих документов. ИТ делопроизводства и документооборота. Электронный документооборот.

Документооборот - это создание первичных учетных документов или получение их от других организаций, их принятие к учету, обработка, передача в архив. Движение первичных документов в бухгалтерском учете регламентируется графиком документооборота.

График документооборота - это график или схема, которые описывают движение первичных документов на предприятии от момента их создания до момента передачи на хранение.
Унифицированной формы графика документооборота нет. Каждое предприятие составляет график самостоятельно, исходя из особенностей деятельности.

Разрабатывает график документооборота главный бухгалтер, а утверждает руководитель предприятия.

Дата добавления: 2015-06-26