Средняя арифметическая

Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, деленной на число этих значений.

Отдельные значения признака называют вариантами и обозначают через ; число единиц совокупности обозначают через n, среднее значение признака - через . Следовательно, средняя арифметическая простая равна:

Средняя арифметическая взвешенная вычисляется по формуле:

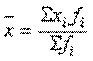
где 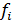- частота повторения i-ых вариантов признака, называемая весом. Таким образом, средняя арифметическая взвешенная равна сумме взвешенных вариантов признака, деленная на сумму весов.

Она применяется в тех случаях, когда каждая варианта признака встречается несколько (неравное) число раз.

Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами. В таких рядах условно величина интервала первой группы принимается равной величине интервала последующей, а величина интервала последней группы - величине интервала предыдущей. Дальнейший расчет аналогичен изложенному выше.

При расчете средней по интервальному вариационному ряду необходимо сначала найти середину интервалов. Это и будут значения 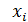, а количество единиц совокупности в каждой группе 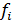(таблица 1.2.2).

Пример

Таблица 1.2.3

Возраст рабочего, лет	Число рабочих, чел ()	Середина возрастного интервала, лет ()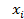
20-30 30-40 40-50 50-60 60 и более
Итого		Х

Средний возраст рабочих цеха будет равен:

лет

Средняя арифметическая обладает рядом свойств, знание которых необходимо для понимания сущности средних, а также для упрощения их вычисления.

1. Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических величин:

Если 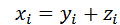, то

.

Это правило показывает, в каких случаях можно суммировать средние величины.

Пример. Выпускаемые изделия состоят из двух деталей y и z и на изготовление каждой из них расходуется y=3 ч, z=5 ч, то средние затраты времени на изготовление одного изделия (x), будут равны:

3+5=8 ч, т. е. x=y+z.

2. Алгебраическая сумма отклонений индивидуальных значений варьирующего признака от средней равна нулю, так как сумма отклонений в одну сторону погашается суммой отклонений в другую, т. е. , потому что:

.

Это правило показывает, что средняя является равнодействующей.

3. Если все варианты ряда уменьшить или увеличить на одно и то же число a, то средняя уменьшится или увеличится на это же число a:

.

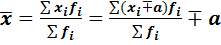4. Если все варианты ряда уменьшить или увеличить в A раз, то средняя также уменьшится или увеличится в A раз:

.

5. Если все частоты ряда разделить или умножить на одно и то же число d, то средняя не изменится:

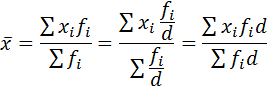
Это свойство показывает, что средняя зависит не от размеров весов, а от соотношения между ними. Следовательно, в качестве весов могут выступать не только абсолютные, но и относительные величины.[3, 80 с.]

Дата добавления: 2015-06-26