
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие средних величин и их виды. Правило мажорантности средних
|
|
|
|
Тема 4. Средние числа и показатели вариации
План
1. Понятие средних величин и их виды.Правило мажорантности средних.
2. Структурные средние.
3. Показатели вариации.
Средняя величина является одним из самых распространенных обобщающих показателей в статистике, только с помощью средней можно охарактеризовать совокупность по количественному варьирующему признаку.
С помощью средних величин можно сравнивать между собой различные совокупности по варьирующим признакам. Средняя величина всегда обобщает количественную вариацию признака. Характеристики средних величин: обобщающая величина; именованная величина; абстрактная величина; как, правило средняя величина не совпадает ни с одним из вариантов; исчисляется по однородным, однокачественным явлениям.
Виды средних величин.
Существуют различные виды средних величин. В статистике применяют степенные средние и структурные средние. К степенным средним относят: арифметическую, квадратическую, кубическую, гармоническую, геометрическую.
К структурным средним относят квантили (медиана, квартили, децили, процентили и др.) распределения и моду.
Степенные средние делятся на простые и взвешенные. Простая применяется тогда, когда у каждой варианте частота равна единице. Взвешенная применяется тогда, когда каждый вариант встречается в совокупности одинаковое число раз. Степенные средние представлены в табл.4. Таблица 4
Степенные средние
| № | Вид степенной средней | Показа-тель степени (m) | Формула расчета | |
| Простая (для несгруппированных данных | Взвешенная (для сгруппированных данных) | |||
Арифметическая
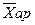
|
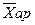 = ∑X: n = ∑X: n
|
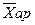 = ∑Xf: ∑f = ∑Xf: ∑f
| ||
Квадратическая
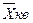
|
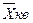 = =  ∑Х²: n ∑Х²: n
|
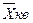 = √∑Х² f: ∑f = √∑Х² f: ∑f
| ||
Гармоническая
 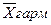
| -1 |
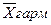 .= n: ∑1/Х; .= n: ∑1/Х;
|
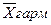 = ∑ w: ∑ w /Х = ∑ w: ∑ w /Х
| |
Геометрическая


|
 = = 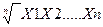
|
 = √ Х1f. Х2 f …Х n f = √ Х1f. Х2 f …Х n f
|
Из степенных средних в статистике наиболее часто применяется средняя арифметическая: простая арифметическая - когда веса отсутствуют или их трудно определить и арифметическая взвешенная вычисляется, когда значения осредняемого признака повторяются (встречаются несколько раз).
С редняя квадратическая наиболее широко используется при расчете показателей вариации.
Реже применяется средняя гармоническая (обратная средней арифметической) исчисляется в тех случаях, когда в качестве весов применяются не единицы совокупности, а произведение этих единиц на значение признака w = Хf.
С редняя геометрическая применяется, когда необходимо вчислить средние темпы роста.
Разные виды степенных средних при одном и том же исходном материале имеют неодинаковое значение. Чем больше показатель степени средней в формуле степенной средней, тем больше величина средней. Это правило называется правилом мажорантности средних.
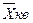 >
> 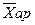 .>
.>  >
> 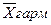
| х | х² | 1/х |
| 1/3 | ||
| 1/6 |
Пример:
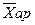 .=(3+6):2 = 4,5, Х кв. = √(9 +36):2 = 4,75;
.=(3+6):2 = 4,5, Х кв. = √(9 +36):2 = 4,75; 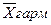 = 2: (1/3 +1/6) =12:3= 4,
= 2: (1/3 +1/6) =12:3= 4,  . = √3х6 = 4,26
. = √3х6 = 4,26
К структурным характеристикам распределния варьирующего признака относят квантили распределения (медиану, квартили, децили и др.) и моду.
Квантиль – это значение признака Х, занимающее определенное место в упорядоченной по данному признаку совокупности. Виды квантилей:
Медиана (Ме) – это вариант, делящий совокупность пополам, т.е. серединная варианта, варианта, находящяяся в середине вариационного ряда. Она делит ряд пополам, по обе стороны от нее (верх и вниз находится одинаковое количество единиц совокупности.
Квартили – значения признака, делящие упорядоченную совокупность на 4 равные части;
Децили - значения признака, делящие упорядоченную совокупность на 10 равных частей;
Процентили – значения признака, делящие упорядоченную совокупность на 100 равных частей.
Медиана показывает количественную границу значения варьирующего признака, которую достигла половина членов совокупности.
Мода– это вариант, который чаще всего встречается в совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту.
Мода и медиана отличаются от степенных средних тем, что являются конкретными характеристиками, их значение имеет какая – либо конкретная варианта в вариационном ряду.
Мода применяется в тех случаях, когда нужно охарактеризовать наиболее часто встречающуюся величину признака. Например, надо узнать наиболее распространенный размер з/платы на предприятии.
Мода и медиана являются типичными характеристиками в тех случаях, когда взяты совокупности однородные и большой численности.
Пример. Распределение семей по числу детей
| Группа семей по числу детей | Число семей Накопленные частоты |
| 10 10 | |
| 30 40 | |
| Мода - 2 | 75 115 |
| 45 160 | |
| 20 180 | |
| 15 195 | |
| 6 201 | |
| Итого | 201 - |
Мода - это семья, имеющая двоих детей, т.к этому значению варианты соответствует наибольшее число семей.
Если распределения, где все варианты встречаются одинаково часто, в этом случае моды нет или все варианты одинаково модальны. Если две варианты могут иметь наибольшие частоты, тогда будут две моды, распределение будет бимодальным.
Чтобы найти медиану в дискретном вариационном ряду, нужно сумму частот разделить пополам и к полученному результату добавить ½. Так, в распределении 201 семьи по числу детей медианой будет: 201/2 + ½ = 101, т.е. 101-я варианта, которая делит упорядоченный ряд пополам. Чтобы вычислить значение 101 варианты, нужно накапливать частоты, начиная с наименьшей варианты. 101 варианта соответствует третьему значению варьирующего признака, и медианой будет семья, имеющая двоих детей. В этом примере медиана и мода совпали.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 15856; Нарушение авторских прав?; Мы поможем в написании вашей работы!