
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выделяют дисперсию общую, групповую и межгрупповую
|
|
|
|
Общая дисперсия была разобрана выше, простая и взвешенная. Она отражает вариацию признака за счет всех условий и причин, действующих в совокупности.
Групповая (частная) дисперсия измеряет вариацию внутри группы. Она тоже может быть простой и взвешенной. σi² = ∑(Х- 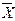 ) ²ni / ∑ni
) ²ni / ∑ni
Средняя из внутригрупповых (частных) дисперсий – это средняя арифметическая взвешенная из дисперсий групповых: σi² = ∑σ²i ni∑ni – это средняя отражает случайную вариацию.
Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних от общей средней δ² =∑(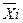 -
- 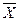 )²: n – характеризует вариацию результативного признака за счет группировочного признака. δ² = ∑(
)²: n – характеризует вариацию результативного признака за счет группировочного признака. δ² = ∑(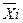 -
- 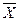 )²: ∑f i – межгрупповая дисперсия измеряет вариацию между частными совокупностями.
)²: ∑f i – межгрупповая дисперсия измеряет вариацию между частными совокупностями. 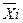 -средняя по каждой отдельной группе,
-средняя по каждой отдельной группе, 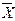 -средняя по всей совокупности.
-средняя по всей совокупности.
При δ² = 0 можно утверждать, что связь между изучаемыми признаками отсутствует.
Между указанными видами дисперсий существует определенное соотношение: Правило сложения дисперсий. Сложив среднюю внутригрупповых дисперсий с дисперсией групповых средних, получим общую дисперсию. Общая дисперсия признака всегда равна средней внутригрупповых дисперсий плюс дисперсия групповых средних.
σ²о = σi² + δ²- Зная две величины всегда можно определить третью величину. Зная, общую дисперсию и дисперсию групповых средних, можно судить о силе влияния группировочного признака. σо² = σi² + δ²
σо² - общая дисперсия, σi² - средняя из частных дисперсия,
δ² – межгрупповая дисперсия
Пример. Имеются данные о производительности труда за час работы, представленные в табл.
Групповая дисперсия – 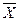 1= 90:6 = 15
1= 90:6 = 15 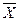 2= 126: 6 = 21
2= 126: 6 = 21
Средняя из групповых σi² = 10:6= 1,67 σi² = 28:6 = 4,66
σi²=/(1,67 х 6) +(4,66 х6)/: 12 = (10 +28): 12 = 38:12=3,16
| №таб.раб. | Изготовлено продукции за час х | Х- 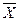
| (Х- 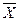 )² )²
| №таб.раб. | Изгото влено продукции за час х | Х- 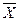
| (Х- 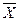 )² )²
|
| -2 | -3 | ||||||
| -1 | -2 | ||||||
| -1 | |||||||
Межгрупповая дисперсия. Средняя взвешенная из групповых средних –
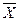 = (15х6 +21х6): 12 =(90 +126):12 = 18
= (15х6 +21х6): 12 =(90 +126):12 = 18
δ²= /(15-18)²х6 +(21-18)² х6/: 12=108:12= 9
Общая дисперсия по правилу сложений дисперсий: σо²= 3,16 +9 = 12,16
Проверим общую дисперсию обычным способом: σо² = (13-18)² +(14- 18)²…+(23-18)²: 12 = 146:12= 12,16
Правило сложения дисперсий используется в статистике для определения степени связи между изучаемыми признаками. Степень влияния признака – фактора, положенного в основание группировки, можно измерить при помощи либо коэффициента детерминации, либо эмпирического корреляционного отношения.
Коэффициент детерминации η²: - показывает какая доля всей вариации признака обусловлена признаком, положенным в основание группировки.
η² = δ²: σо²
Корень из коэффициента детерминации называют эмпирическим корреляционным отношением –: η - показывает тесноту связи между признаками группировочным и результативным. Это отношение может принимать значения от 0 до 1. η= √δ²: σо²
Пример: На 2- м курсе экономического факультета одного из ВУЗов есть 2 группы студентов. В 1-й группе занимаются студенты после окончания колледжа, во 2-й группе – после школы. По результатам зимней экзаменационной сессии сделаем расчет общей, частной и межгрупповой дисперсий, а также степень влияния на оценку студента наличие или отсутствие спец.эконом. подготовки.
Расчет общей, частной, групповой и межгрупповой дисперсий
| № группы | Сред-ний балл xi | Число сту-ден-тов ni | Средне-квадра- тическое отклоне- ние в группе σi | Групп-повая (част- ная) диспер- сия σi² | xi ni | σi² ni |
(xi–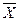 ) )
|
(xi–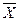 ) ² ) ²
| (xi–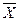 ) ² ni ) ² ni
|
| 3,6 | 0,1 | 0,01 | 86,4 | 0,24 | 0,24 | 0,057 | 1,368 | ||
| 3,1 | 0,2 | 0,04 | 65,1 | 0,84 | 0,26 | 0,0676 | 1,4196 | ||
| 151,5 | 1,08 | 0,1252 | 2,7876 |
Найдем общий средний балл на курсе 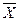 = (∑xi ni): ∑ ni = 151,5:45 = 3,36 Среднюю из групповых (частных) дисперсий определим по формуле:
= (∑xi ni): ∑ ni = 151,5:45 = 3,36 Среднюю из групповых (частных) дисперсий определим по формуле:
σi² = ∑ σi² ni: ∑ ni = 1,08:45= 0,024
Межгрупповая дисперсия равна: δ²= ∑(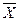 i–
i– 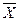 ) ² ni: ∑ ni = 2,7876: 45 = 0,0619
) ² ni: ∑ ni = 2,7876: 45 = 0,0619
Тогда общая дисперсия по правилу сложения дисперсий составит:σо² = σi² + δ² = 0,024 + 0,0619 = 0,0859. Следовательно, фактор положенный в основу группировки, существенно влияет на средний балл студента (на его успеваемость).
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 2770; Нарушение авторских прав?; Мы поможем в написании вашей работы!